Building a model of the impact grinding mechanism in a tumbling mill based on data visualization
DOI:
https://doi.org/10.15587/1729-4061.2023.283073Keywords:
tumbling mill, intra-chamber loading, impact action, flight zone, similarity criteria, grinding performanceAbstract
A mathematical model was built based on data visualization for the impact grinding mechanism in a tumbling mill, which is mainly implemented during coarse grinding.
The determination of impulse interaction parameters is problematic due to the difficulty of modeling and the complexity of hardware analysis of the behavior of intramill loading.
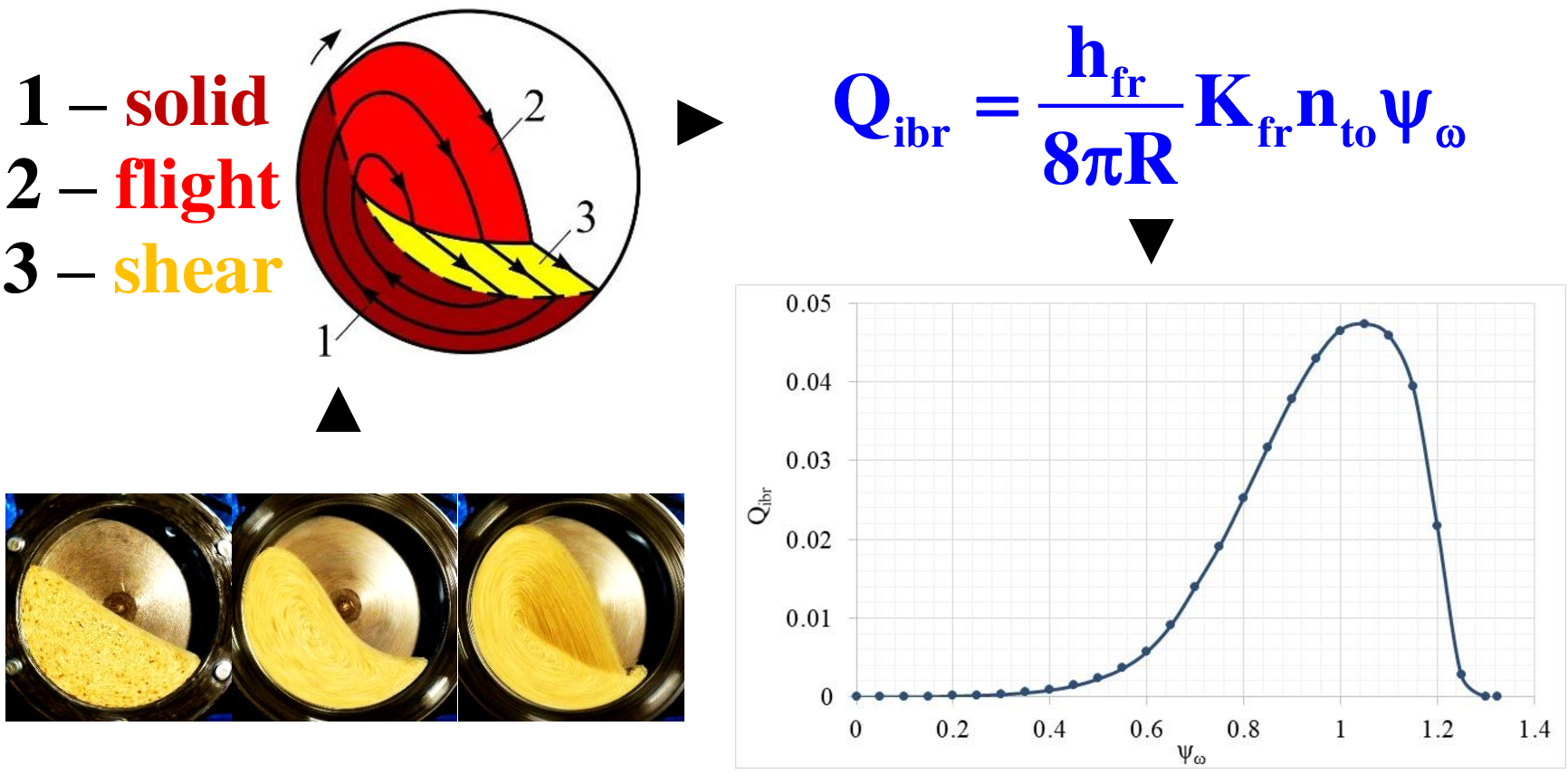
Conceptually, it was envisaged to identify the relative dynamic parameters of the impact action as components of the model, which are criteria for the similarity of the loading movement and the grinding process. Impact power was taken as an analog of grinding performance. The initial characteristic of the impact was considered to be the averaged vertical component of the speed of loading movement in the flight zone at the boundary of contact with the shear layer. The formalization of the model revealed the effect on the performance of the mass fraction of the flight zone and the reversibility of loading.
The method of numerical modeling was applied, based on experimental visualization of the behavior of granular loading in the cross section of a rotating chamber.
The influence of the rotation speed on the performance at a chamber filling degree of 0.45 and a relative particle size of a milling load of 0.0104 was estimated by experimental simulation. The maximum productivity value was found at the relative speed of rotation ψω=1–1.05. A rational condition for impact grinding at ψω=0.75–0.9 has been established.
The test proved the effectiveness of using visualization to evaluate dynamic loading interaction analogs. Verification of modeling results was implemented by comparison with the data of the technical standard. The use of similarity criteria unifies approaches to modeling different mechanisms of destruction.
The model built makes it possible to predict the rational parameters of the grinding processes by impact, crushing, and abrasion
References
- Fuerstenau, D. W., Abouzeid, A.-Z. M. (2002). The energy efficiency of ball milling in comminution. International Journal of Mineral Processing, 67 (1-4), 161–185. doi: https://doi.org/10.1016/s0301-7516(02)00039-x
- Tromans, D. (2008). Mineral comminution: Energy efficiency considerations. Minerals Engineering, 21 (8), 613–620. doi: https://doi.org/10.1016/j.mineng.2007.12.003
- Napier-Munn, T. (2015). Is progress in energy-efficient comminution doomed? Minerals Engineering, 73, 1–6. doi: https://doi.org/10.1016/j.mineng.2014.06.009
- Bouchard, J., LeBlanc, G., Levesque, M., Radziszewski, P., Georges-Filteau, D. (2019). Breaking down energy consumption in industrial grinding mills. CIM Journal, 10 (4), 157–164. doi: https://doi.org/10.15834/cimj.2019.18
- Chimwani, N. (2021). A Review of the Milestones Reached by the Attainable Region Optimisation Technique in Particle Size Reduction. Minerals, 11 (11), 1280. doi: https://doi.org/10.3390/min11111280
- Cleary, P. W. (2001). Charge behaviour and power consumption in ball mills: sensitivity to mill operating conditions, liner geometry and charge composition. International Journal of Mineral Processing, 63 (2), 79–114. doi: https://doi.org/10.1016/s0301-7516(01)00037-0
- Morrison, R. D., Cleary, P. W. (2008). Towards a virtual comminution machine. Minerals Engineering, 21 (11), 770–781. doi: https://doi.org/10.1016/j.mineng.2008.06.005
- Bilgili, E., Scarlett, B. (2005). Population balance modeling of non-linear effects in milling processes. Powder Technology, 153 (1), 59–71. doi: https://doi.org/10.1016/j.powtec.2005.02.005
- Wills, B. A., Finch, J. (2015). Wills' mineral processing technology: An introduction to the practical aspects of ore treatment and mineral recovery. Butterworth-Heinemann. doi: https://doi.org/10.1016/c2010-0-65478-2
- Gupta, V. K. (2020). Energy absorption and specific breakage rate of particles under different operating conditions in dry ball milling. Powder Technology, 361, 827–835. doi: https://doi.org/10.1016/j.powtec.2019.11.033
- Datta, A., Mishra, B. K. (1999). Power draw estimation of ball mills using neural networks. Mining, Metallurgy & Exploration, 16 (1), 57–60. doi: https://doi.org/10.1007/bf03402857
- Rezaeizadeh, M., Fooladi, M., Powell, M. S., Mansouri, S. H. (2010). Experimental observations of lifter parameters and mill operation on power draw and liner impact loading. Minerals Engineering, 23 (15), 1182–1191. doi: https://doi.org/10.1016/j.mineng.2010.07.017
- Soleymani, M. M., Fooladi, M., Rezaeizadeh, M. (2016). Experimental investigation of the power draw of tumbling mills in wet grinding. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 230 (15), 2709–2719. doi: https://doi.org/10.1177/0954406215598801
- Góralczyk, M., Krot, P., Zimroz, R., Ogonowski, S. (2020). Increasing Energy Efficiency and Productivity of the Comminution Process in Tumbling Mills by Indirect Measurements of Internal Dynamics—An Overview. Energies, 13 (24), 6735. doi: https://doi.org/10.3390/en13246735
- Golpayegani, M. H., Rezai, B. (2022). Modelling the power draw of tumbling mills: A comprehensive review. Physicochemical Problems of Mineral Processing. doi: https://doi.org/10.37190/ppmp/151600
- Govender, I Powell, M. S. (2006). An empirical power model derived from 3D particle tracking experiments. Minerals Engineering, 19 (10), 1005–1012. doi: https://doi.org/10.1016/j.mineng.2006.03.017
- Bbosa, L. S., Govender, I., Mainza, A. N., Powell, M. S. (2011). Power draw estimations in experimental tumbling mills using PEPT. Minerals Engineering, 24 (3-4), 319–324. doi: https://doi.org/10.1016/j.mineng.2010.10.005
- Bbosa, L. S., Govender, I., Mainza, A. (2016). Development of a novel methodology to determine mill power draw. International Journal of Mineral Processing, 149, 94–103. doi: https://doi.org/10.1016/j.minpro.2016.02.009
- Tohry, A., Chehreh Chelgani, S., Matin, S. S., Noormohammadi, M. (2020). Power-draw prediction by random forest based on operating parameters for an industrial ball mill. Advanced Powder Technology, 31 (3), 967–972. doi: https://doi.org/10.1016/j.apt.2019.12.012
- Tavares, L. M. (2017). A Review of Advanced Ball Mill Modelling. KONA Powder and Particle Journal, 34, 106–124. doi: https://doi.org/10.14356/kona.2017015
- Kelly, E. G., Spottiswood, D. J. (1982). Introduction to mineral processing. Wiley- Interscience.
- King, R. P. (2001). Modeling and simulation of mineral processing systems. Elsevier. doi: https://doi.org/10.1016/c2009-0-26303-3
- Chieregati, A. C., Delboni Júnior, H. (2001). Novo método de caracterização tecnológica para cominuição de minérios. São Paulo: EPUSP.
- Gupta, A., Yan, D. (2016). Mineral processing design and operations: An introduction. Elsevier. doi: https://doi.org/10.1016/c2014-0-01236-1
- Yin, Z., Peng, Y., Zhu, Z., Yu, Z., Li, T. (2017). Impact Load Behavior between Different Charge and Lifter in a Laboratory-Scale Mill. Materials, 10 (8), 882. doi: https://doi.org/10.3390/ma10080882
- Boateng, A. A., Barr, P. V. (1996). Modelling of particle mixing and segregation in the transverse plane of a rotary kiln. Chemical Engineering Science, 51 (17), 4167–4181. doi: https://doi.org/10.1016/0009-2509(96)00250-3
- Ding, Y. L., Forster, R., Seville, J. P. K., Parker, D. J. (2002). Granular motion in rotating drums: bed turnover time and slumping–rolling transition. Powder Technology, 124 (1-2), 18–27. doi: https://doi.org/10.1016/s0032-5910(01)00486-7
- Mellmann, J. (2001). The transverse motion of solids in rotating cylinders—forms of motion and transition behavior. Powder Technology, 118 (3), 251–270. doi: https://doi.org/10.1016/s0032-5910(00)00402-2
- Rajchenbach, J. (1990). Flow in powders: From discrete avalanches to continuous regime. Physical Review Letters, 65 (18), 2221–2224. doi: https://doi.org/10.1103/physrevlett.65.2221
- Zik, O., Levine, D., Lipson, S. G., Shtrikman, S., Stavans, J. (1994). Rotationally Induced Segregation of Granular Materials. Physical Review Letters, 73 (5), 644–647. doi: https://doi.org/10.1103/physrevlett.73.644
- Orpe, A. V., Khakhar, D. V. (2001). Scaling relations for granular flow in quasi-two-dimensional rotating cylinders. Physical Review E, 64 (3). doi: https://doi.org/10.1103/physreve.64.031302
- Taberlet, N., Richard, P., Hinch, E. J. (2006). S shape of a granular pile in a rotating drum. Physical Review E, 73 (5), 050301. doi: https://doi.org/10.1103/physreve.73.050301
- Govender, I., Richter, M. C., Mainza, A. N., De Klerk, D. N. (2016). A positron emission particle tracking investigation of the scaling law governing free surface flows in tumbling mills. AIChE Journal, 63 (3), 903–913. doi: https://doi.org/10.1002/aic.15453
- Yin, Z., Peng, Y., Li, T., Wu, G. (2018). DEM Investigation of Mill Speed and Lifter Face Angle on Charge Behavior in Ball Mills. IOP Conference Series: Materials Science and Engineering, 394, 032084. doi: https://doi.org/10.1088/1757-899x/394/3/032084
- Maleki-Moghaddam, M., Yahyaei, M., Banisi, S. (2013). A method to predict shape and trajectory of charge in industrial mills. Minerals Engineering, 46-47, 157–166. doi: https://doi.org/10.1016/j.mineng.2013.04.013
- Powell, M. S McBride, A. T. (2004). A three-dimensional analysis of media motion and grinding regions in mills. Minerals Engineering, 17 (11-12), 1099–1109. doi: https://doi.org/10.1016/j.mineng.2004.06.022
- Morrison, A. J., Govender, I., Mainza, A. N., Parker, D. J. (2016). The shape and behaviour of a granular bed in a rotating drum using Eulerian flow fields obtained from PEPT. Chemical Engineering Science, 152, 186–198. doi: https://doi.org/10.1016/j.ces.2016.06.022
- de Klerk, D. N., Govender, I., Mainza, A. N. (2019). Geometric features of tumbling mill flows: A positron emission particle tracking investigation. Chemical Engineering Science, 206, 41–49. doi: https://doi.org/10.1016/j.ces.2019.05.020
- Naumenko, Y. (2017). Modeling a flow pattern of the granular fill in the cross section of a rotating chamber. Eastern-European Journal of Enterprise Technologies, 5 (1 (89)), 59–69. doi: https://doi.org/10.15587/1729-4061.2017.110444
- Naumenko, Y. (2017). Modeling of fracture surface of the quasi solid-body zone of motion of the granular fill in a rotating chamber. Eastern-European Journal of Enterprise Technologies, 2 (1 (86)), 50–57. doi: https://doi.org/10.15587/1729-4061.2017.96447
- Naumenko, Y., Sivko, V. (2017). The rotating chamber granular fill shear layer flow simulation. Eastern-European Journal of Enterprise Technologies, 4 (7 (88)), 57–64. doi: https://doi.org/10.15587/1729-4061.2017.107242
- Deineka, K., Naumenko, Y. (2019). Revealing the effect of decreased energy intensity of grinding in a tumbling mill during self-excitation of auto-oscillations of the intrachamber fill. Eastern-European Journal of Enterprise Technologies, 1 (1), 6–15. doi: https://doi.org/10.15587/1729-4061.2019.155461
- Deineka, K., Naumenko, Y. (2020). Establishing the effect of decreased power intensity of self-oscillatory grinding in a tumbling mill when the crushed material content in the intra-chamber fill is reduced. Eastern-European Journal of Enterprise Technologies, 4 (1 (106)), 39–48. doi: https://doi.org/10.15587/1729-4061.2020.209050
- Deineka, K., Naumenko, Y. (2019). Establishing the effect of a decrease in power intensity of self-oscillating grinding in a tumbling mill with a reduction in an intrachamber fill. Eastern-European Journal of Enterprise Technologies, 6 (7 (102)), 43–52. doi: https://doi.org/10.15587/1729-4061.2019.183291
- Deineka, K., Naumenko, Y. (2021). Establishing the effect of a simultaneous reduction in the filling load inside a chamber and in the content of the crushed material on the energy intensity of self-oscillatory grinding in a tumbling mill. Eastern-European Journal of Enterprise Technologies, 1 (1 (109)), 77–87. doi: https://doi.org/10.15587/1729-4061.2021.224948
- Deineka, K., Naumenko, Y. (2022). Revealing the mechanism of stability loss of a two-fraction granular flow in a rotating drum. Eastern-European Journal of Enterprise Technologies, 4 (1 (118)), 34–46. doi: https://doi.org/10.15587/1729-4061.2022.263097
- Deineka, K. Yu., Naumenko, Yu. V. (2018). The tumbling mill rotation stability. Scientific Bulletin of National Mining University, 1, 60–68. doi: https://doi.org/10.29202/nvngu/2018-1/10
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Yuriy Naumenko, Kateryna Deineka

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








