Розробка математичних та комп’ютерних моделей розрахунку контактних характеристик взаємодії жорсткого штампа з пружним півпростором

Автор(и)

  • Тетяна Анатоліївна Зайцева Дніпровський національний університет імені Олеся Гончара, Україна https://orcid.org/0000-0002-6346-3390
  • Владислав Вікторович Жушман Дніпровський національний університет імені Олеся Гончара, Україна https://orcid.org/0009-0000-7292-5879

DOI:

https://doi.org/10.15587/1729-4061.2024.302792

Ключові слова:

просторова контактна задача, аналітичний розв’язок, метод скінченних елементів, ANSYS, CLIPS

Анотація

Об’єктом дослідження є система штамп-пружний півпростір, що знаходиться під дією стискаючої сили. В роботі розв’язано проблему визначення контактних напружень і переміщень. Змістом отриманих результатів є побудовані моделі, оцінка їх адекватності.

В роботі розглянуто задачу про тиснення на однорідний та ізотропний пружний півпростір абсолютно жорсткого плоского двозв’язного штампа. Для отримання аналітичного розв’язку, застосовано варіант метода збурень заснований на розкладанні за малим параметром потенціала простого шару, розподіленого по двозв’язній області. Виконано зведення задачі про тиснення плоского штампу у формі некругового кільця до послідовності задач для штампа у формі кругового кільця. Це дозволило використовувати відоме рішення для кругового кільця.

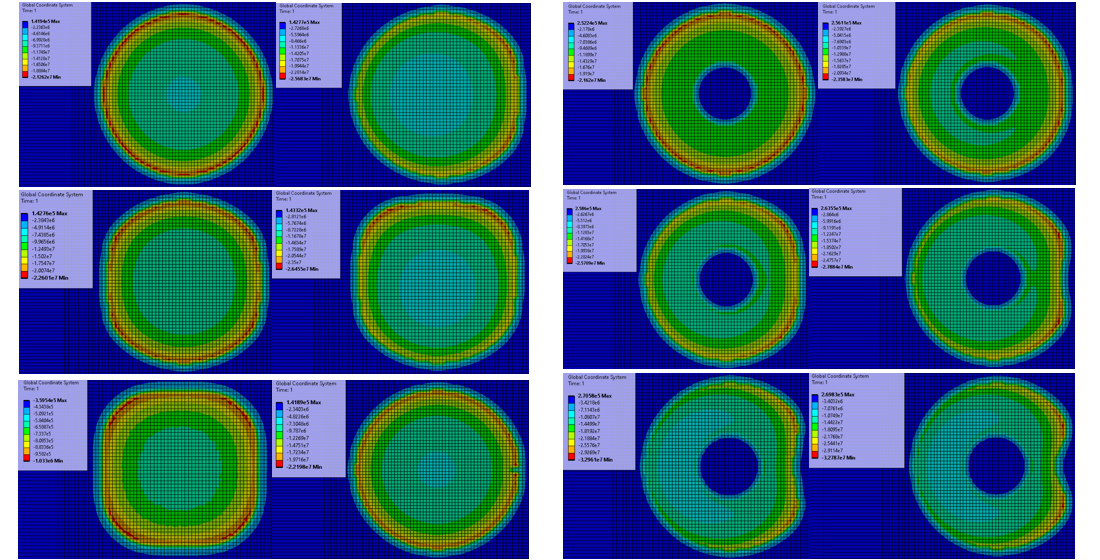
За допомогою системи ANSYS побудовано скінченно-елементні моделі. Створено групу моделей для врахування можливих пошкоджень у разі перебування системи штамп-пружній півпростір в складних природних умовах або в агресивному середовищі за певний час модельного застосування. Таким чином сформовано базу даних з метою подальшої передачі її у програмний інструмент CLIPS. Створено набори правил та знань.

В процесі дослідження розроблено узагальнюючий алгоритм для задач побудови та аналізу математичних і комп’ютерних моделей контактної взаємодії жорсткого циліндричного штампу із плоскою двозв’язною основою з пружнім півпростором під дією стискаючої сили. Вирішена задача визначення геометричної форми поперечного перерізу кільцевого в плані штампа для системи штамп-пружний півпростір у разі, коли зона контакту не відома заздалегіть. Побудований підхід може бути застосовано в інженерних розрахунках на міцність та довговічність

Біографії авторів

Тетяна Анатоліївна Зайцева, Дніпровський національний університет імені Олеся Гончара

Кандидат технічних наук, доцент, завідувачка кафедри

Кафедра комп’ютерних технологій

Владислав Вікторович Жушман, Дніпровський національний університет імені Олеся Гончара

Аспірант

Кафедра комп’ютерних технологій

Посилання

  1. Liu, W. K., Li, S., Park, H. S. (2022). Eighty Years of the Finite Element Method: Birth, Evolution, and Future. Archives of Computational Methods in Engineering, 29 (6), 4431–4453. https://doi.org/10.1007/s11831-022-09740-9
  2. Yilmaz, K. B., Comez, I., Yildirim, B., Güler, M. A., El-Borgi, S. (2018). Frictional receding contact problem for a graded bilayer system indented by a rigid punch. International Journal of Mechanical Sciences, 141, 127–142. https://doi.org/10.1016/j.ijmecsci.2018.03.041
  3. Bonari, J., Marulli, M. R., Hagmeyer, N., Mayr, M., Popp, A., Paggi, M. (2019). A multi-scale FEM-BEM formulation for contact mechanics between rough surfaces. Computational Mechanics, 65 (3), 731–749. https://doi.org/10.1007/s00466-019-01791-3
  4. Gladwell, G. M. L. (Eds.) (2008). Contact Problems – the legacy of L.A. Galin. Springer, 318. https://doi.org/10.1007/978-1-4020-9043-1
  5. Loboda, V., Shevelova, N., Khodanen, T., Lapusta, Y. (2022). An interaction of electrically conductive and electrically permeable collinear cracks in the interface of piezoelectric materials. Archive of Applied Mechanics, 92 (5), 1465–1480. https://doi.org/10.1007/s00419-022-02123-3
  6. Guz, A. N., Zozulya, V. V. (2002). Elastodynamic unilateral contact problems with friction for bodies with crack. International Applied Mechanics, 38 (8), 895–932. https://doi.org/10.1023/a:1021266113662
  7. Myshkin, N. K., Goryacheva, I. G., Grigoriev, A. Ya., Kavaliova, I. N., Makhovskaya, Yu. Yu. (2020). Contact Interaction in Precision Tribosystems. Journal of Friction and Wear, 41 (3), 191–197. https://doi.org/10.3103/s1068366620030113
  8. Li, B., Li, P., Zhou, R., Feng, X.-Q., Zhou, K. (2022). Contact mechanics in tribological and contact damage-related problems: A review. Tribology International, 171, 107534. https://doi.org/10.1016/j.triboint.2022.107534
  9. Roitman, A. B., Shishkanova, S. F. (1973). The solution of the annular punch problem with the aid of recursion relations. Soviet Applied Mechanics, 9 (7), 725–729. https://doi.org/10.1007/bf00882996
  10. Shishkanova, S. F. (1990). Stress state of an elastic half-space weakened by a plane crack which is close to being annular. Soviet Applied Mechanics, 26 (5), 430–435. https://doi.org/10.1007/bf00887257
  11. Shyshkanova, G., Zaуtseva, T., Frydman, O. (2015). The analysis of manufacturing errors effect on contact stresses distribution under the ring parts deformed asymmetrically. Metallurgical and Mining Industry, 7, 352–357. Available at: https://www.metaljournal.com.ua/assets/Journal/english-edition/MMI_2015_7/055Shyshkanova-352-357.pdf
  12. Shyshkanova, G. (2018). About Stability of First Kind Equation Solving. 2018 IEEE First International Conference on System Analysis & Intelligent Computing (SAIC). https://doi.org/10.1109/saic.2018.8516805
  13. Babich, S. Yu., Guz, A. N., Rudnitskii, V. B. (2004). Contact Problems for Prestressed Elastic Bodies and Rigid and Elastic Punches. International Applied Mechanics, 40 (7), 744–765. https://doi.org/10.1023/b:inam.0000046219.34646.4e
  14. Babych, S. Yu., Yarets’ka, N. O. (2021). Contact Problem for an Elastic Ring Punch and a Half-Space with Initial (Residual) Stresses*. International Applied Mechanics, 57 (3), 297–305. https://doi.org/10.1007/s10778-021-01081-7
  15. Yarets’ka, N. (2023). Contact Problems for Cylindrical Stamps and Elastic Bodies with Initial (Residual) Stresses. Advanced Structured Materials, 517–546. https://doi.org/10.1007/978-3-031-37313-8_29
  16. Zare, I., Allen, M. S. (2021). Adapting a contact-mechanics algorithm to predict damping in bolted joints using quasi-static modal analysis. International Journal of Mechanical Sciences, 189, 105982. https://doi.org/10.1016/j.ijmecsci.2020.105982
  17. Wang, F., Wei, H. (2018). Virtual element method for simplified friction problem. Applied Mathematics Letters, 85, 125–131. https://doi.org/10.1016/j.aml.2018.06.002
  18. Shyshkanova, G., Walther, A. (2023). Simple layer potential expansion for optimization of contact interaction taking into account friction and adhesion. Journal of Physics: Conference Series, 2675 (1), 012033. https://doi.org/10.1088/1742-6596/2675/1/012033
  19. Guk, N. A., Obodan, N. I. (2014). An Algorithm for the Solution of the Inverse Problem of the Theory of Shells. Journal of Mathematical Sciences, 198 (2), 192–203. https://doi.org/10.1007/s10958-014-1783-5
  20. Obodan, N. I., Zaitseva, T. A., Fridman, O. D. (2019). Contact Problem for a Rigid Punch and an Elastic Half Space as an Inverse Problem. Journal of Mathematical Sciences, 240 (2), 184–193. https://doi.org/10.1007/s10958-019-04346-2
  21. Shyshkanova, G., Zaytseva, T., Zhushman, V., Levchenko, N., Korotunova, O. (2023). Solving three-dimensional contact problems for foundation design in green building. Journal of Physics: Conference Series, 2609 (1), 012001. https://doi.org/10.1088/1742-6596/2609/1/012001
  22. Free Student Software Downloads. Ansys. Available at: https://www.ansys.com/academic/students?utm_source=ie&utm_medium=video2&utm_campaign=freedownload
  23. Obodan, N., Guk, N., Kozakova, N. (2017). Identification of the additional exposure zone for ensuring a complete contact of the two-layered system. Eastern-European Journal of Enterprise Technologies, 5 (7 (89)), 23–29. https://doi.org/10.15587/1729-4061.2017.109674
  24. Guk, N. A., Kozakova, N. L. (2021). Delamination of a Three-Layer Base Under the Action of Normal Loading. Journal of Mathematical Sciences, 254 (1), 89–102. https://doi.org/10.1007/s10958-021-05290-w
  25. CLIPS. A Tool For Building Expert Systems. Available at: https://www.clipsrules.net/
  26. Banichuk, N. V., Ivanova, S. Yu. (2017). Optimal Structural Design. De Gruyter. https://doi.org/10.1515/9783110531183
  27. Zhou, Y., Lin, Q., Hong, J., Yang, N. (2020). Combined interface shape and material stiffness optimization for uniform distribution of contact stress. Mechanics Based Design of Structures and Machines, 51 (2), 1001–1015. https://doi.org/10.1080/15397734.2020.1860086
  28. Kress, R. (1989). Tikhonov Regularization. Applied Mathematical Sciences, 243–258. https://doi.org/10.1007/978-3-642-97146-4_16
  29. Gutman, E. M. (1994). Mechanochemistry of Solid Surfaces. World Scientific. https://doi.org/10.1142/2373
  30. Dolinskiy, V. M. (1975). Izgib tonkih plastin, podverzhennyh korrozionnomu iznosu. Dinamika i prochnost' mashin, 21, 43–49.
Розробка математичних та комп’ютерних моделей розрахунку контактних характеристик взаємодії жорсткого штампа з пружним півпростором

##submission.downloads##

Опубліковано

2024-04-30

Як цитувати

Зайцева, Т. А., & Жушман, В. В. (2024). Розробка математичних та комп’ютерних моделей розрахунку контактних характеристик взаємодії жорсткого штампа з пружним півпростором. Eastern-European Journal of Enterprise Technologies, 2(7 (128), 67–78. https://doi.org/10.15587/1729-4061.2024.302792

Номер

Том 2 № 7 (128) (2024): Прикладна механіка

Розділ

Прикладна механіка

Ліцензія

Авторське право (c) 2024 Tetyana Zaytseva, Vladyslav Zhushman

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.