Identification of the pulse axisymmetric load acting on a composite cylindrical shell, inhomogeneous in length, made of different materials
DOI:
https://doi.org/10.15587/1729-4061.2022.265356Keywords:
cylindrical shell, nonstationary deformation, inverse problem, integral equation, Tikhonov regularizationAbstract
The problem of identifying the load acting on the elements of structures belongs to the class of inverse problems of the mechanics of a deformable solid, which are often incorrect. Solving such problems is associated with the instability of the calculation results, which requires the development of special methods for their research. This predetermines the relevance of this study.
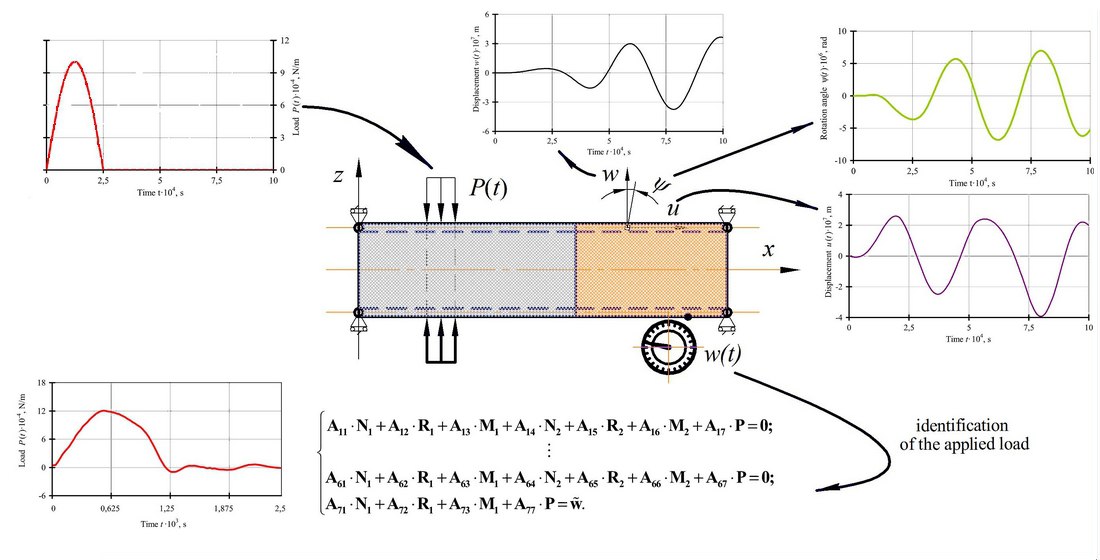
The object of the study is a single-pass cylindrical shell consisting of two rigidly fastened butt-fastened sections made of different materials. Each of the shells is assumed to be elastic isotropic, having a cross-section of medium thickness. The equations of axisymmetric deformation of shells are used within the framework of Timoshenko hypotheses.
An approach to solving direct and inverse problems for such discretely heterogeneous objects is proposed, which implies the conditional separation of a discretely heterogeneous cylindrical shell along the length, followed by the addition of functions of fictitious loads. The main analytical relationships for building a system of integral Volterra equations are given, for which an analytic-numerical solution is derived.
The final ratios have been obtained, which make it possible to calculate the kinematic and force parameters of the study object in the process of non-stationary deformation. The inverse problem of identifying arbitrary loads acting on a shell that is heterogeneous in length is solved in a general form. An algorithm for the restoration of pulse loads has been developed, which is robust to errors in the initial data (about 5 %).
The material related to solving direct and inverse problems for shells that are discretely heterogeneous in length can significantly advance the methodology for identifying pulse loads acting on structural elements
References
- Vatul'yan, A. O., Solov'ev, A. N. (2008). Pryamye i obratnye zadachi dlya odnorodnykh i neodnorodnykh uprugikh i elektrouprugikh tel. Rostov-na-Donu, 176.
- Timoshenko, S. P., Voynovskiy-Kriger, S. (1966). Plastinki i obolochki. Moscow: Nauka, 635.
- Grigolyuk, E. I., Selezov, I. T. (1973). Mekhanika tverdykh deformiruemykh tel. T. 5. Neklassicheskie teorii kolebaniy sterzhney, plastin i obolochek. Moscow: VINITI, 272.
- Ramm, A. G. (2005). Inverse problems: mathematical and analytical techniques with applications to engineering. Springer, 442. doi: https://doi.org/10.1007/b100958
- Samarskiy, A. A., Vabischevich, P. N. (2004). CHislennye metody resheniya obratnykh zadach matematicheskoy fiziki. Moscow: Editorial URSS, 480.
- Tikhonov A. N., Arsenin V. Ya. (1986). Metody resheniya nekorrektnykh zadach. Moscow: Nauka, 288.
- Iakovlev, S., Santos, H. A. F. A., Williston, K., Murray, R., Mitchell, M. (2013). Non-stationary radiation by a cylindrical shell: Numerical modeling using the Reissner–Mindlin theory. Journal of Fluids and Structures, 36, 50–69. doi: https://doi.org/10.1016/j.jfluidstructs.2012.09.003
- Krivenko, O., Vorona, Y. (2018). Analysis of non-stationary reaction of elastic shell to impulse load. Strength of Materials and Theory of Structures, 101, 26–37. doi: https://doi.org/10.32347/2410-2547.2018.101.26-37
- Smetankina, N., Kravchenko, I., Merculov, V., Ivchenko, D., Malykhina, A. (2020). Modelling of Bird Strike on an Aircraft Glazing. Advances in Intelligent Systems and Computing, 289–297. doi: https://doi.org/10.1007/978-3-030-37618-5_25
- Smetankina, N., Merkulova, A., Merkulov, D., Postnyi, O. (2021). Dynamic Response of Laminate Composite Shells with Complex Shape Under Low-Velocity Impact. Integrated Computer Technologies in Mechanical Engineering - 2020, 267–276. doi: https://doi.org/10.1007/978-3-030-66717-7_22
- Smetankina, N. V., Merkulova, A. I., Postnyi, O. V., Merkulov, D. O., Misura, S. Yu. (2021). Optimal Design of Layered Cylindrical Shells with Minimum Weight Under Impulse Loading. 2021 IEEE 2nd KhPI Week on Advanced Technology (KhPIWeek). doi: https://doi.org/10.1109/khpiweek53812.2021.9569982
- Lugovoi, P. Z., Sirenko, V. N., Skosarenko, Yu. V., Batutina, T. Ya. (2017). Dynamics of a Discretely Reinforced Cylindrical Shell Under a Local Impulsive Load. International Applied Mechanics, 53 (2), 173–180. doi: https://doi.org/10.1007/s10778-017-0803-9
- Lugovoi, P. Z., Meish, Yu. A. (2016). Nonstationary Deformation of Longitudinally and Transversely Reinforced Cylindrical Shells on an Elastic Foundation. International Applied Mechanics, 52 (1), 62–72. doi: https://doi.org/10.1007/s10778-016-0733-y
- Lugovoi, P. Z., Meish, V. F. (2017). Dynamics of Inhomogeneous Shell Systems Under Non-Stationary Loading (Survey). International Applied Mechanics, 53 (5), 481–537. doi: https://doi.org/10.1007/s10778-017-0833-3
- Skosarenko, Yu. V. (2015). The Stress–Strain State of a Ribbed Cylindrical Shell Interacting with an Elastic Foundation Under Short-Term Loads. International Applied Mechanics, 51 (1), 92–101. doi: https://doi.org/10.1007/s10778-015-0675-9
- Davar, A., Azarafza, R., Fayez, M. S., Fallahi, S., Jam, J. E. (2021). Dynamic Response of a Grid-Stiffened Composite Cylindrical Shell Reinforced with Carbon Nanotubes to a Radial Impulse Load. Mechanics of Composite Materials, 57 (2), 181–204. doi: https://doi.org/10.1007/s11029-021-09944-3
- Wang, J.-P., Mao, Y.-J., Di, F., Lü, J., Huang, H.-J. (2016). Comparative analysis of transient responses of cylindrical shells induced by moving and simultaneous impulsive loads. Gaoya Wuli Xuebao/Chinese Journal of High Pressure Physics, 30, 491–498. doi: https://doi.org/10.11858/gywlxb.2016.06.009
- Konstantinov, A. Y., Kochetkov, A. V., Krylov, S. V., Smirnov, I. V. (2016). Simulation the dynamics of a composite cylindrical shell with a gas-permeable layer under the internal impulse loading. Materials physics and mechanics, 28 (1/2), 39–42.
- Heydarpour, Y., Mohammadzaheri, M., Ghodsi, M., Soltani, P., Al-Jahwari, F., Bahadur, I., Al-Amri, B. (2021). A coupled DQ-Heaviside-NURBS approach to investigate nonlinear dynamic response of GRE cylindrical shells under impulse loads. Thin-Walled Structures, 165, 107958. doi: https://doi.org/10.1016/j.tws.2021.107958
- Huang, Z., Yu, X. (2022). Numerical Simulation Study of Expanding Fracture of 45 Steel Cylindrical Shell under Different Detonation Pressure. Materials, 15 (11), 3980. doi: https://doi.org/10.3390/ma15113980
- Ji, C., Long, Y., Fang, X., Liu, Q., Gao, F.-Y. (2013). Dynamic response and perforation failure of cylindrical shell subjected to lateral local impulsive loading. Zhendong yu Chongji/Journal of Vibration and Shock, 32.
- Voropay, A. V., Povalyaev, S. I., Sharapata, A. S., Yanyutin, E. G. (2005). Primenenie teorii integral'nykh uravneniy Vol'terra pri reshenii dinamicheskikh obratnykh zadach dlya plastin i obolochek. Vestnik Khar'kovskogo natsional'nogo universiteta. Seriya: Matematychne modeliuvannia. Informatsiyni tekhnolohiyi. Avtomatyzovani systemy upravlinnia, 661, 69–82.
- Yanyutin, E. G., Povalyaev, S. I. (2005). Nekorrektnye zadachi impul'snogo deformirovaniya dlya tsilindricheskoy obolochki. Vestnik natsional'nogo tekhnicheskogo universiteta "KhPI",22, 129–138.
- Yanyutin, E. G., Povalyaev, S. I. (2008). Identification of nonstationary axisymmetric load distributed along a cylindrical shell. International Applied Mechanics, 44 (7), 794–801. doi: https://doi.org/10.1007/s10778-008-0093-3
- Egorov, P. A. (2014). Identifikatsiya nestatsionarnykh nagruzok, vozdeystvuyuschikh na sharnirno-opertuyu obolochku, podkreplennuyu kontsentricheskimi rebrami zhestkosti. Visnyk NTU «KhPI». Seriya: Matematychne modeliuvannia v tekhnitsi ta tekhnolohiyakh, 39 (1082), 71–80.
- Yanyutin, Ye. G., Gnatenko, G. A., Yegorov, P. A. (2018). Nonstationary deformation of reinforced cylindrical shells. Bulletin of the National Technical University "KhPI". Ser.: Mathematical modeling in engineering and technologies, 27 (1303), 148–156. Available at: http://repository.kpi.kharkov.ua/handle/KhPI-Press/40827
- Yanyutin, E. G., Gnatenko, G. A. (2010). Identifikatsiya nagruzki, vozdeystvuyuschey na sostavnuyu balku. Visnyk Kharkivskoho natsionalnoho avtomobilno-dorozhnoho universytetu, 49, 93–97.
- Voropai, A. V., Yanyutin, E. G. (2007). Identification of several impulsive loads on a plate. International Applied Mechanics, 43 (7), 780–785. doi: https://doi.org/10.1007/s10778-007-0078-7
- Ditkin, V. A., Prudnikov, A. P. (1966). Operatsionnoe ischislenie. Moscow: Vysshaya shkola, 405.
- Voropay, A. V. (2018). Integral'nye uravneniya Vol'terra v nekorrektnykh zadachakh nestatsionarnogo deformirovaniya plastin. Kharkiv: Izd-vo «Lider», 212. Available at: http://repository.kpi.kharkov.ua/bitstream/KhPI-Press/41162/1/Book_2018_Voropay_Integr_uravneniya.pdf
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2022 Alexey Voropay, Grygoriy Gnatenko, Pavlo Yehorov, Serhii Povaliaiev, Olena Naboka

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








