Numerical solutions for crack problems during elastomer forming

Authors

DOI:

https://doi.org/10.15587/1729-4061.2022.268285

Keywords:

rubber crack, rubber pad, numerical analysis, elastomer forming, crack propagation, ABAQUS

Abstract

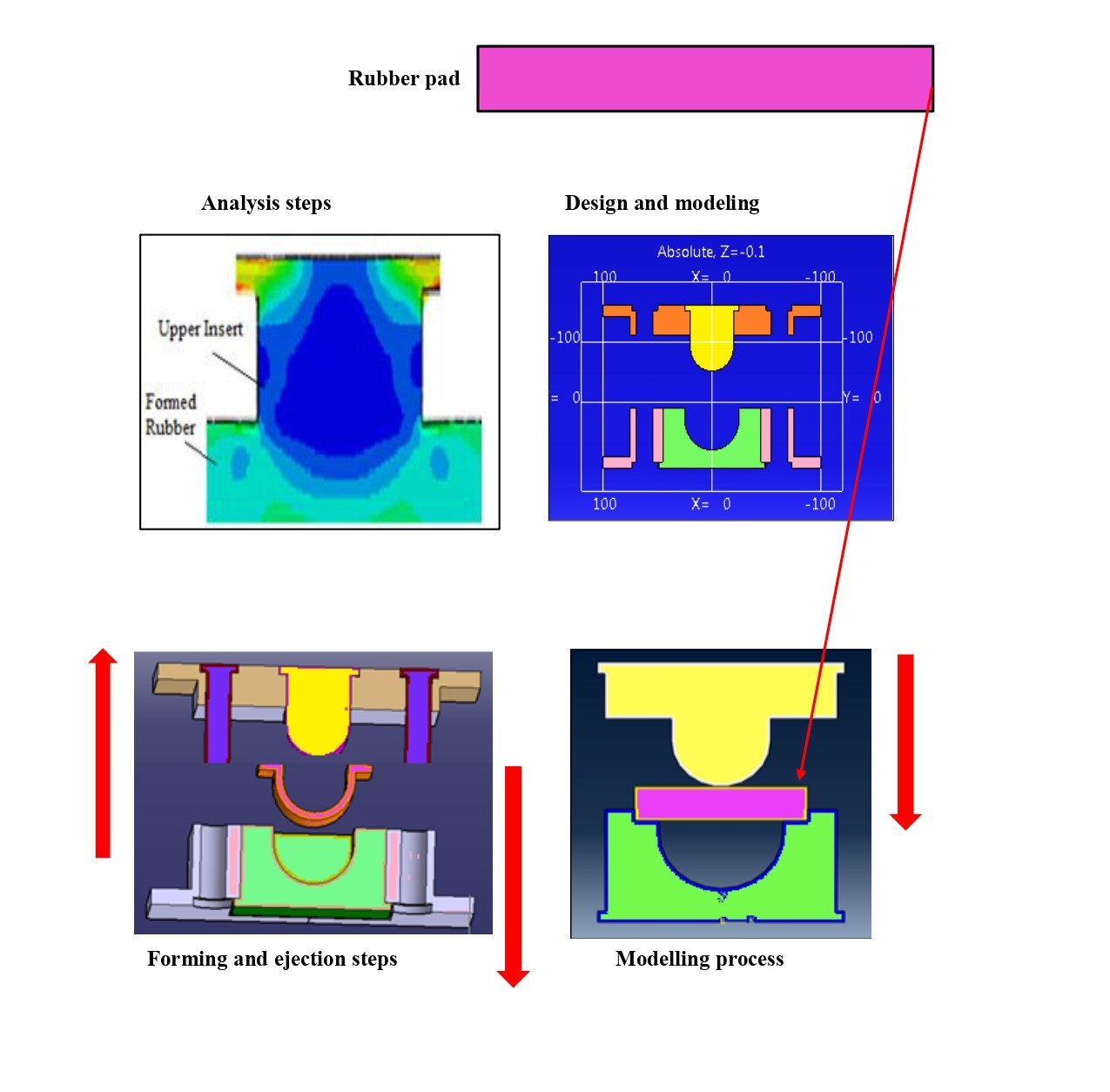
Generically, thermoset elastomers are often referred to as rubber. It is characterized by the chemical bonding between polymer chains. One of the important problems that plague elastomer manufacturing and rubber parts under service is cracks. Predicting the main factors affecting crack propagation trajectories during forming and after curing time is an important challenge. For this purpose, numerical analysis was implemented by using the commercial ABAQUS/CAE software package. A three-dimensional model was established to predict the important factors that affect this process. During the analysis, the effect of forming velocity and the amount of kinetic energy on the distortion of rubber material and crack propagation is explored in detail by using different forming punch velocities. The drop velocity of the upper insert (punch) on the rubber pad was taken as 10 m/s, 7 m/s, and 5 m/s, respectively. Consequently, while each forming velocity will generate different kinetic energy between the interaction surfaces, the change in crack behavior and the normal stress can be monitored in different positions. As a result, among these velocities, it was found that the low forming velocity of the upper insert (punch) is better than the others in forming rubber where cracks and distortions were at minimum values. Also, the amount of kinetic energy is low enough in the case of low speeds and can affect the results significantly. In addition, it was found that the generated stresses have a significant impact on the crack development in a specific area, especially near the fillets and sharp edges. It was concluded that calculating the parameters affecting the crack growth and predicting the crack propagation trajectories using the finite element method is a significant method for predicting and solving crack problems before tool fabrication

Author Biographies

Badr Kamoon, Al-Furat Al-Awsat Technical University

Master Science in Mechanical and Manufacturing System Engineering

Department of Machinery and Equipment Engineering

Salam O. Dahi, Al-Furat Al-Awsat Technical University

Master Science in Mechanical and Manufacturing System Engineering

Department of Machinery and Equipment Engineering

Hamzah Kadhim, Al-Furat Al-Awsat Technical University

Master Science in Mechanical Engineering

Department of Mechanical

Karbala Technical Institute

References

  1. Scetta, G. (2020). Fatigue cracking of thermoplastic elastomers. Université Paris sciences et lettres. Available at: https://pastel.archives-ouvertes.fr/tel-03149063
  2. Samarth, N. B., Mahanwar, P. A. (2021). Degradation of Polymer & Elastomer Exposed to Chlorinated Water – A Review. Open Journal of Organic Polymer Materials, 11 (01), 1–50. doi: https://doi.org/10.4236/ojopm.2021.111001
  3. Corre, T., Coret, M., Verron, E., Leblé, B. (2021). Non steady-state intersonic cracks in elastomer membranes under large static strain. Journal of Theoretical, Computational and Applied Mechanics. doi: https://doi.org/10.46298/jtcam.6906
  4. Poulain, X., Lefèvre, V., Lopez-Pamies, O., Ravi-Chandar, K. (2017). Damage in elastomers: nucleation and growth of cavities, micro-cracks, and macro-cracks. International Journal of Fracture, 205 (1), 1–21. doi: https://doi.org/10.1007/s10704-016-0176-9
  5. Wang, H., Wu, Y., Yang, J., Wang, H. (2021). Numerical Simulation on Reflective Cracking Behavior of Asphalt Pavement. Applied Sciences, 11 (17), 7990. doi: https://doi.org/10.3390/app11177990
  6. Hamzah, K. B., Nik Long, N. M. A., Senu, N., Eshkuvatov, Z. K. (2021). Numerical Solution for Crack Phenomenon in Dissimilar Materials under Various Mechanical Loadings. Symmetry, 13 (2), 235. doi: https://doi.org/10.3390/sym13020235
  7. Halkacı, H. S., Öztürk, E., Türköz, M., Dilmeç, M. (2017). 2D Finite Element Analysis of Rubber Pad Forming Process. 2 nd International Conference on Science, Ecology and Technology-2016 (ICONSETE’2016). Available at: https://www.researchgate.net/publication/312198030
  8. Oscar, J., Centeno, G. (2017). Finite Element Modeling Of Rubber Bushing For Crash Simulation Experimental Tests and Validation. Division of Structural Mechanics, Lund University. Available at: https://www.byggmek.lth.se/fileadmin/byggnadsmekanik/publications/tvsm5000/web5163.pdf
  9. Iváñez, I., Braun, M. (2017). Numerical analysis of surface cracks repaired with single and double patches of composites. Journal of Composite Materials, 52 (8), 1113–1120. doi: https://doi.org/10.1177/0021998317722044
  10. Elmukashfi, E., Kroon, M. (2020). Numerical Modeling and Analysis of Dynamic Crack Propagation in Rubber. 13th International Conference on Fracture. Beijing. Available at: https://www.researchgate.net/publication/346898728
  11. Magid, H. M., Dabis, B. K., Abed alabas Siba, M. (2021). Analysis of the main factors affecting mass production in the plastic molding process by using the finite element method. Eastern-European Journal of Enterprise Technologies, 6 (1 (114)), 65–71. doi: https://doi.org/10.15587/1729-4061.2021.248375
  12. Kadhim, K. J., Jaber, J. A., Ibrihim, H. R. (2022). Implementation of finite element analysis for solving the constraints in forming process of large steel parts. Eastern-European Journal of Enterprise Technologies, 4 (1 (118)), 64–71. doi: https://doi.org/10.15587/1729-4061.2022.263452
  13. Persson, B. N. J., Albohr, O., Heinrich, G., Ueba, H. (2005). Crack propagation in rubber-like materials. Journal of Physics: Condensed Matter, 17 (44), R1071–R1142. doi: https://doi.org/10.1088/0953-8984/17/44/r01
  14. Elmukashfi, E. (2015). Modeling of fracture and damage in rubber under dynamic and quasi-static conditions. School of Engineering Sciences, Department of Solid Mechanics, Royal Institute of Technology. Stockholm. Available at: http://kth.diva-portal.org/smash/get/diva2:876354/FULLTEXT01.pdf
  15. Maiorova, K., Vorobiov, I., Andrieiev, O., Lupkin, B., Sikulskiy, V. (2022). Forming the geometric accuracy and roughness of holes when drilling aircraft structures made from polymeric composite materials. Eastern-European Journal of Enterprise Technologies, 2 (1 (116)), 71–80. doi: https://doi.org/10.15587/1729-4061.2022.254555
  16. Korzhyk, V., Khaskin, V., Grynyuk, A., Peleshenko, S., Kvasnytskyi, V., Fialko, N. et al. (2022). Comparison of the features of the formation of joints of aluminum alloy 7075 (Al-Zn-Mg-Cu) by laser, microplasma, and laser-microplasma welding. Eastern-European Journal of Enterprise Technologies, 1 (12 (115)), 38–47. doi: https://doi.org/10.15587/1729-4061.2022.253378
Numerical solutions for crack problems during elastomer forming

Downloads

Published

2022-12-30

How to Cite

Kamoon, B., O. Dahi, S., & Kadhim, H. (2022). Numerical solutions for crack problems during elastomer forming . Eastern-European Journal of Enterprise Technologies, 6(1 (120), 83–90. https://doi.org/10.15587/1729-4061.2022.268285

Issue

Vol. 6 No. 1 (120) (2022): Engineering technological systems

Section

Engineering technological systems

License

Copyright (c) 2022 Badr Kamoon, Salam O. Dahi, Hamzah Kadhim

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.