Чисельні рішення проблем утворення тріщин при формуванні еластомеру

Автор(и)

DOI:

https://doi.org/10.15587/1729-4061.2022.268285

Ключові слова:

тріщини в каучуку, гумова прокладка, чисельний аналіз, формування еластомеру, поширення тріщин, ABAQUS

Анотація

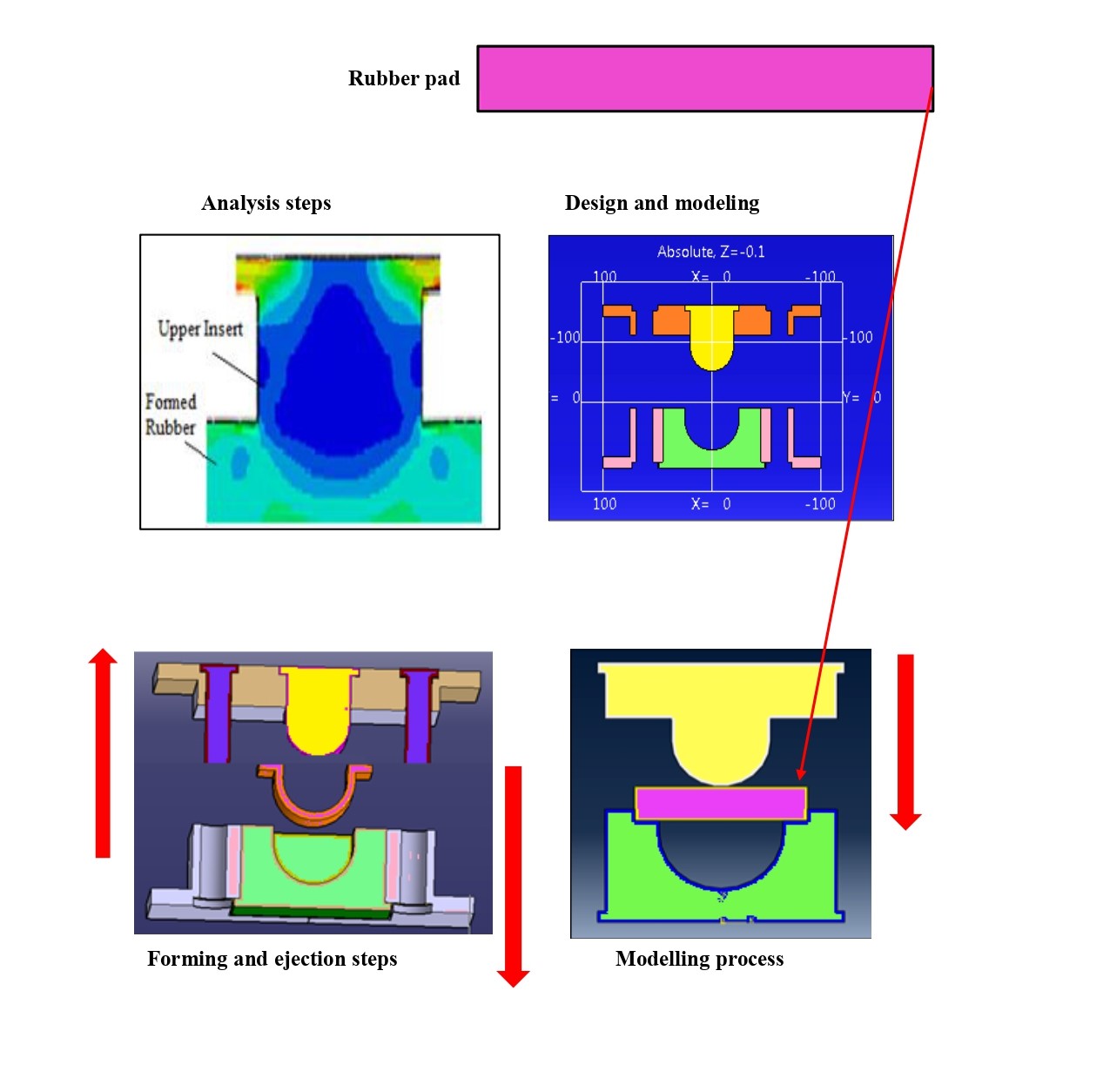
Термореактивні еластомери часто називають каучуком. Він характеризується хімічним зв’язком між полімерними ланцюгами. Однією з істотних проблем, з якими стикаються виробники еластомерів та експлуатовані деталі з каучуку, є утворення тріщин. Важливим завданням є прогнозування основних факторів, що впливають на траєкторії поширення тріщин під час формування та після затвердіння. Для цієї мети було проведено чисельний аналіз з використанням комерційного програмного пакету ABAQUS/CAE. Для прогнозування важливих факторів, що впливають на цей процес, була створена тривимірна модель. Аналіз детально вивчає вплив швидкості формування та кількості кінетичної енергії на деформацію каучукового матеріалу та поширення тріщин за допомогою різних швидкостей штампування. Швидкість падіння верхньої вставки (пуансона) на гумову прокладку прийнята рівною 10 м/с, 7 м/с та 5 м/с відповідно. Отже, у той час як кожна швидкість формування генеруватиме різну кінетичну енергію між поверхнями взаємодії, зміну поведінки тріщин і нормальне напруження можна відстежувати в різних положеннях. В результаті було виявлено, що серед даних швидкостей кращою є низька швидкість формування верхньої вставки (пуансона) при формуванні каучуку з мінімальними значеннями тріщин і деформацій. Крім того, кількість кінетичної енергії досить невелика у разі низьких швидкостей і може суттєво вплинути на результати. Також встановлено, що створювані напруження мають значний вплив на розвиток тріщин у певній області, особливо поблизу заокруглень і гострих кромок. Зроблено висновок, що розрахунок параметрів, що впливають на ріст тріщин, та прогнозування траєкторій поширення тріщин за допомогою методу кінцевих елементів є важливим способом прогнозування та вирішення проблем утворення тріщин до виготовлення інструменту

Біографії авторів

Badr Kamoon, Al-Furat Al-Awsat Technical University

Master Science in Mechanical and Manufacturing System Engineering

Department of Machinery and Equipment Engineering

Salam O. Dahi, Al-Furat Al-Awsat Technical University

Master Science in Mechanical and Manufacturing System Engineering

Department of Machinery and Equipment Engineering

Hamzah Kadhim, Al-Furat Al-Awsat Technical University

Master Science in Mechanical Engineering

Department of Mechanical

Karbala Technical Institute

Посилання

  1. Scetta, G. (2020). Fatigue cracking of thermoplastic elastomers. Université Paris sciences et lettres. Available at: https://pastel.archives-ouvertes.fr/tel-03149063
  2. Samarth, N. B., Mahanwar, P. A. (2021). Degradation of Polymer & Elastomer Exposed to Chlorinated Water – A Review. Open Journal of Organic Polymer Materials, 11 (01), 1–50. doi: https://doi.org/10.4236/ojopm.2021.111001
  3. Corre, T., Coret, M., Verron, E., Leblé, B. (2021). Non steady-state intersonic cracks in elastomer membranes under large static strain. Journal of Theoretical, Computational and Applied Mechanics. doi: https://doi.org/10.46298/jtcam.6906
  4. Poulain, X., Lefèvre, V., Lopez-Pamies, O., Ravi-Chandar, K. (2017). Damage in elastomers: nucleation and growth of cavities, micro-cracks, and macro-cracks. International Journal of Fracture, 205 (1), 1–21. doi: https://doi.org/10.1007/s10704-016-0176-9
  5. Wang, H., Wu, Y., Yang, J., Wang, H. (2021). Numerical Simulation on Reflective Cracking Behavior of Asphalt Pavement. Applied Sciences, 11 (17), 7990. doi: https://doi.org/10.3390/app11177990
  6. Hamzah, K. B., Nik Long, N. M. A., Senu, N., Eshkuvatov, Z. K. (2021). Numerical Solution for Crack Phenomenon in Dissimilar Materials under Various Mechanical Loadings. Symmetry, 13 (2), 235. doi: https://doi.org/10.3390/sym13020235
  7. Halkacı, H. S., Öztürk, E., Türköz, M., Dilmeç, M. (2017). 2D Finite Element Analysis of Rubber Pad Forming Process. 2 nd International Conference on Science, Ecology and Technology-2016 (ICONSETE’2016). Available at: https://www.researchgate.net/publication/312198030
  8. Oscar, J., Centeno, G. (2017). Finite Element Modeling Of Rubber Bushing For Crash Simulation Experimental Tests and Validation. Division of Structural Mechanics, Lund University. Available at: https://www.byggmek.lth.se/fileadmin/byggnadsmekanik/publications/tvsm5000/web5163.pdf
  9. Iváñez, I., Braun, M. (2017). Numerical analysis of surface cracks repaired with single and double patches of composites. Journal of Composite Materials, 52 (8), 1113–1120. doi: https://doi.org/10.1177/0021998317722044
  10. Elmukashfi, E., Kroon, M. (2020). Numerical Modeling and Analysis of Dynamic Crack Propagation in Rubber. 13th International Conference on Fracture. Beijing. Available at: https://www.researchgate.net/publication/346898728
  11. Magid, H. M., Dabis, B. K., Abed alabas Siba, M. (2021). Analysis of the main factors affecting mass production in the plastic molding process by using the finite element method. Eastern-European Journal of Enterprise Technologies, 6 (1 (114)), 65–71. doi: https://doi.org/10.15587/1729-4061.2021.248375
  12. Kadhim, K. J., Jaber, J. A., Ibrihim, H. R. (2022). Implementation of finite element analysis for solving the constraints in forming process of large steel parts. Eastern-European Journal of Enterprise Technologies, 4 (1 (118)), 64–71. doi: https://doi.org/10.15587/1729-4061.2022.263452
  13. Persson, B. N. J., Albohr, O., Heinrich, G., Ueba, H. (2005). Crack propagation in rubber-like materials. Journal of Physics: Condensed Matter, 17 (44), R1071–R1142. doi: https://doi.org/10.1088/0953-8984/17/44/r01
  14. Elmukashfi, E. (2015). Modeling of fracture and damage in rubber under dynamic and quasi-static conditions. School of Engineering Sciences, Department of Solid Mechanics, Royal Institute of Technology. Stockholm. Available at: http://kth.diva-portal.org/smash/get/diva2:876354/FULLTEXT01.pdf
  15. Maiorova, K., Vorobiov, I., Andrieiev, O., Lupkin, B., Sikulskiy, V. (2022). Forming the geometric accuracy and roughness of holes when drilling aircraft structures made from polymeric composite materials. Eastern-European Journal of Enterprise Technologies, 2 (1 (116)), 71–80. doi: https://doi.org/10.15587/1729-4061.2022.254555
  16. Korzhyk, V., Khaskin, V., Grynyuk, A., Peleshenko, S., Kvasnytskyi, V., Fialko, N. et al. (2022). Comparison of the features of the formation of joints of aluminum alloy 7075 (Al-Zn-Mg-Cu) by laser, microplasma, and laser-microplasma welding. Eastern-European Journal of Enterprise Technologies, 1 (12 (115)), 38–47. doi: https://doi.org/10.15587/1729-4061.2022.253378
Чисельні рішення проблем утворення тріщин при формуванні еластомеру

##submission.downloads##

Опубліковано

2022-12-30

Як цитувати

Kamoon, B., O. Dahi, S., & Kadhim, H. (2022). Чисельні рішення проблем утворення тріщин при формуванні еластомеру . Eastern-European Journal of Enterprise Technologies, 6(1 (120), 83–90. https://doi.org/10.15587/1729-4061.2022.268285

Номер

Том 6 № 1 (120) (2022): Виробничо-технологічні системи

Розділ

Виробничо-технологічні системи

Ліцензія

Авторське право (c) 2022 Badr Kamoon, Salam O. Dahi, Hamzah Kadhim

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.