Construction of a mathematical model of the dynamics of an autonomous mobile robot of variable configuration

Authors

DOI:

https://doi.org/10.15587/1729-4061.2022.269840

Keywords:

autonomous mobile robot, manipulator, mathematical model, dynamics, dynamic parameters relationship

Abstract

This paper considers the construction of a mathematical model of the movement of an autonomous mobile robot (AMR) in variable configuration, taking into account the relationship of the dynamic parameters of a mechanical system.

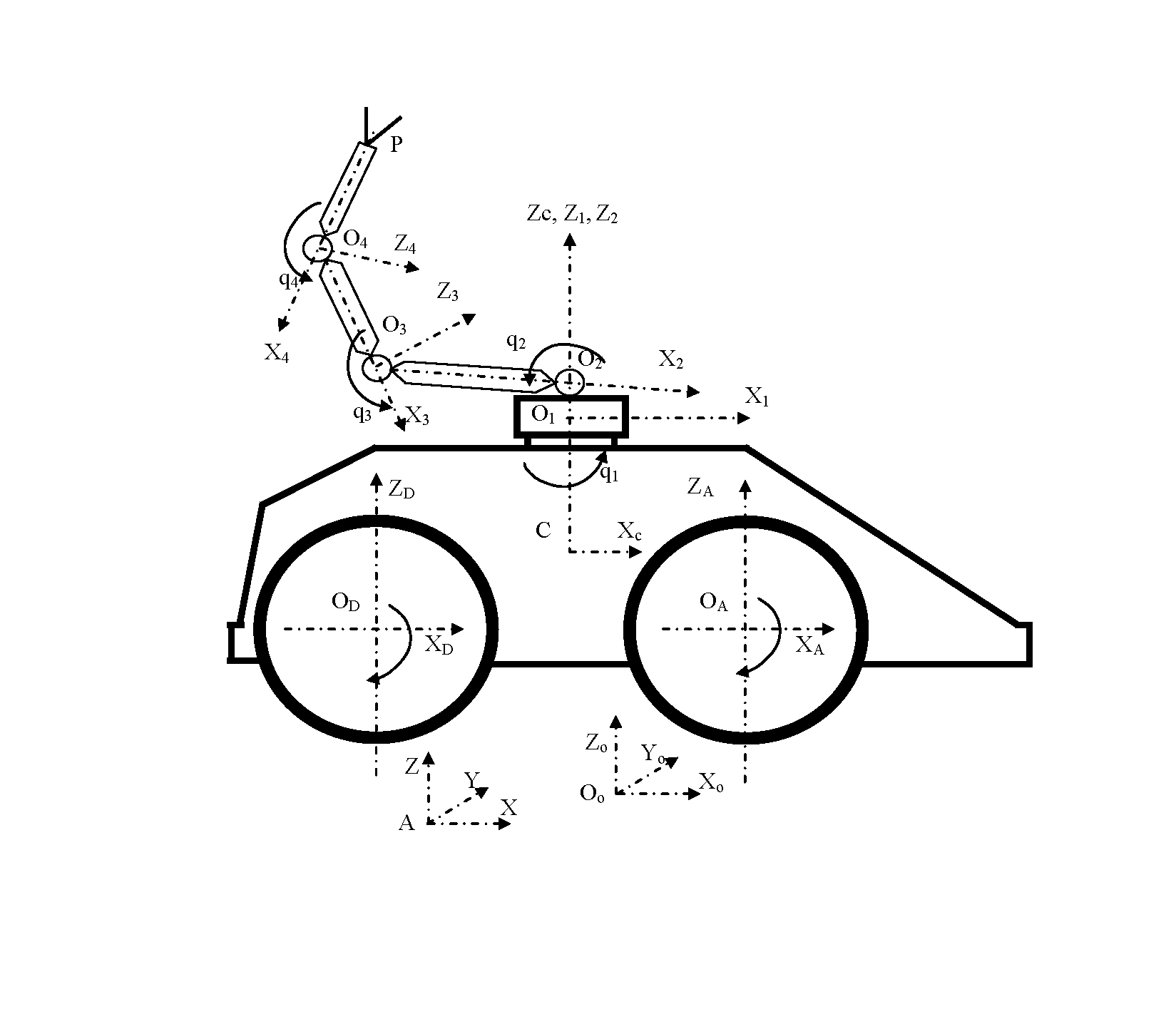
As an example, the design of AMR with a manipulator is considered.

The object of this study is the dynamics of AMR with a manipulator. The peculiarities of the dynamics of AMR with the manipulator are due to the change in the position of the center of mass of the system with the relative movement of the manipulator and the commensurate non-diagonal and diagonal elements of the inertia tensor calculated relative to the axes of the base coordinate system. The construction of the mathematical model was carried out according to the Nyton-Euler method. The resulting mathematical model contains:

– an equation of motion of the center of mass of the AMR system of variable configuration along the trajectory in the inertial coordinate system;

– an equation of angular motion of AMR in variable configuration in the inertial coordinate system;

– an equation of motion of the manipulator with respect to AMR. In a general case, the center of mass of the AMR platform moves in a horizontal plane. Establishing the relationship of dynamic parameters of the mechanical system will make it possible to maintain functionality and ensure the orientation of AMR in vertical planes despite the movement of the manipulator. As an object of control, AMR with a manipulator is a multi-connected system with a cross-internal connection of control channels, which is formed by the dynamic parameters of a mechanical system. Based on the results of mathematical modeling using the proposed model, it is possible to develop algorithms for adaptive control using cross-connection of channels. This will make it possible to identify reserves to reduce energy consumption, increase stability, improve the efficiency and survivability of AMR in variable configuration during autonomous work under extreme conditions.

Author Biography

Natalja Ashhepkova, Oles Honchar Dnipro National University

PhD, Associate Professor

Department of Mechanotronics

References

  1. Lopota, A., Spassky, B. (2020). Mobile ground-based robot systems for professional use. Robotics and Technical Cybernetics, 8 (1), 5–17. doi: https://doi.org/10.31776/rtcj.8101
  2. Tsarichenko, S., Antokhin, E., Chernova, P., Dementey, V. (2020). The state and problems of standardization and unification of military ground robot systems. Robotics and Technical Cybernetics, 8 (1), 18–23. doi: https://doi.org/10.31776/rtcj.8102
  3. Liu, X.-F., Li, H.-Q., Chen, Y.-J., Cai, G.-P. (2015). Dynamics and control of space robot considering joint friction. Acta Astronautica, 111, 1–18. doi: https://doi.org/10.1016/j.actaastro.2015.02.010
  4. Liu, G., Geng, X., Liu, L., Wang, Y. (2019). Haptic based teleoperation with master-slave motion mapping and haptic rendering for space exploration. Chinese Journal of Aeronautics, 32 (3), 723–736. doi: https://doi.org/10.1016/j.cja.2018.07.009
  5. Li, D., Lu, K., Cheng, Y., Zhao, W., Yang, S., Zhang, Y., Li, J., Shi, S. (2020). Dynamic analysis of multi-functional maintenance platform based on Newton-Euler method and improved virtual work principle. Nuclear Engineering and Technology, 52 (11), 2630–2637. doi: https://doi.org/10.1016/j.net.2020.04.017
  6. Sun, H., Zhang, Y., Xue, J., Wu, Z. (2014). The remote control system of the manipulator. Proceedings of the 33rd Chinese Control Conference. doi: https://doi.org/10.1109/chicc.2014.6896388
  7. Korayem, M. H., Shafei, A. M. (2015). Motion equation of nonholonomic wheeled mobile robotic manipulator with revolute-prismatic joints using recursive Gibbs–Appell formulation. Applied Mathematical Modelling, 39 (5-6), 1701–1716. doi: https://doi.org/10.1016/j.apm.2014.09.030
  8. Ashhepkova, N. (2022). Analysis of the inertia tensor of autonomous mobile robot. Technology Audit and Production Reserves, 1 (2 (63)), 36–40. doi: https://doi.org/10.15587/2706-5448.2022.252712
  9. Ashchepkova, N. S. (2020). Algorithm for adaptive control of autonomous mobile robot. Science and Education a New Dimension, VIII (30 (244)), 41–44. doi: https://doi.org/10.31174/SEND-NT2020-244VIII30-10
  10. Ashchepkova, N. S., Ashchepkov, S. A., Kapera, S. S. (2018). Dynamics of transport robot model during the turns. Science and Education a New Dimension, VI (19 (171)), 26–29. doi: https://doi.org/10.31174/send-nt2018-171vi19-05
  11. Chebly, A., Talj, R., Charara, A. (2017). Coupled Longitudinal and Lateral Control for an Autonomous Vehicle Dynamics Modeled Using a Robotics Formalism. IFAC-PapersOnLine, 50 (1), 12526–12532. doi: https://doi.org/10.1016/j.ifacol.2017.08.2190
  12. Mauny, J., Porez, M., Boyer, F. (2017). Symbolic Dynamic Modelling of Locomotion Systems with Persistent Contacts - Application to the 3D Bicycle. IFAC-PapersOnLine, 50 (1), 7598–7605. doi: https://doi.org/10.1016/j.ifacol.2017.08.1007
  13. Ma, Y. (2020). Dynamics of tracked UGVs in three-dimensional space. Dynamics and Advanced Motion Control of Off-Road UGVs, 77–94. doi: https://doi.org/10.1016/b978-0-12-818799-9.00003-7
  14. Gilimyanov, R. F., Pesterev, A. V., Rapoport, L. B. (2008). Motion control for a wheeled robot following a curvilinear path. Journal of Computer and Systems Sciences International, 47 (6), 987–994. doi: https://doi.org/10.1134/s1064230708060129
  15. Bertoncelli, F., Ruggiero, F., Sabattini, L. (2019). Wheel Slip Avoidance through a Nonlinear Model Predictive Control for Object Pushing with a Mobile Robot. IFAC-PapersOnLine, 52 (8), 25–30. doi: https://doi.org/10.1016/j.ifacol.2019.08.043
  16. Ashchepkova, N. S. (2021). Control of a dynamic object with a non-diagonal andnon-stationary inertia tensor moving along a trajectory. Modern engineering and innovative technologies, 18 (2), 44–52. Available at: https://www.moderntechno.de/index.php/meit/issue/view/meit18-02/meit18-02
  17. Bai, S., Zhou, L., Wu, G. (2014). Manipulator Dynamics. Handbook of Manufacturing Engineering and Technology, 1855–1872. doi: https://doi.org/10.1007/978-1-4471-4670-4_91
  18. Ashchepkova, N. S., Sheptun, Yu. D. (1997). Mathematical model of the motion of a space vehicle with a manipulator. Space Science and Technology, 3 (5-6), 34–42. doi: https://doi.org/10.15407/knit1997.05.034
  19. Korayem, M. H., Shafei, A. M., Seidi, E. (2014). Symbolic derivation of governing equations for dual-arm mobile manipulators used in fruit-picking and the pruning of tall trees. Computers and Electronics in Agriculture, 105, 95–102. doi: https://doi.org/10.1016/j.compag.2014.04.013
  20. Lloyd, S., Irani, R., Ahmadi, M. (2021). A numeric derivation for fast regressive modeling of manipulator dynamics. Mechanism and Machine Theory, 156, 104149. doi: https://doi.org/10.1016/j.mechmachtheory.2020.104149
  21. Khurpade, J., Dhami, S. S., Banwait, S. S. (2018). A Virtual Model of 2D Planar Manipulator Dynamics. 2018 International Conference on Smart Systems and Inventive Technology (ICSSIT). doi: https://doi.org/10.1109/icssit.2018.8748674
  22. Tian, S. X., Wang, S. Z. (2011). Dynamic Modeling and Simulation of a Manipulator with Joint Inertia. Information and Automation, 10–16. doi: https://doi.org/10.1007/978-3-642-19853-3_2
  23. Bulhakov, V. M., Yaremenko, V. V., Chernysh, O. M., Berezovyi, M. H. (2019). Teoretychna mekhanika. Kyiv: TsUL, 640.
  24. Kuzo, I. V., Zinko, Ya. A., Vankovych, T.-N. M. et al. (2017). Teoretychna mekhanika. Kharkiv: Folio, 576.
Construction of a mathematical model of the dynamics of an autonomous mobile robot of variable configuration

Downloads

Published

2022-12-30

How to Cite

Ashhepkova, N. (2022). Construction of a mathematical model of the dynamics of an autonomous mobile robot of variable configuration . Eastern-European Journal of Enterprise Technologies, 6(7 (120), 30–44. https://doi.org/10.15587/1729-4061.2022.269840

Issue

Vol. 6 No. 7 (120) (2022): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2022 Natalja Ashhepkova

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.