Construction of spherical non-circular wheels formed by symmetrical arcs of loxodrome
DOI:
https://doi.org/10.15587/1729-4061.2023.272400Keywords:
noncircular wheels, rolling, bevel gear, arc length, spherical curve, loxodromeAbstract
Bevel gears are used to transmit torque between intersecting axes. They demonstrate high reliability and durability of work, as well as a constant gear ratio. The disadvantage of such a transmission is the mutual sliding of the surfaces of the teeth of the gears, which leads to the emergence of friction forces and wear of their working surfaces. In this regard, there is a task to design such bevel gears that would have no slip.
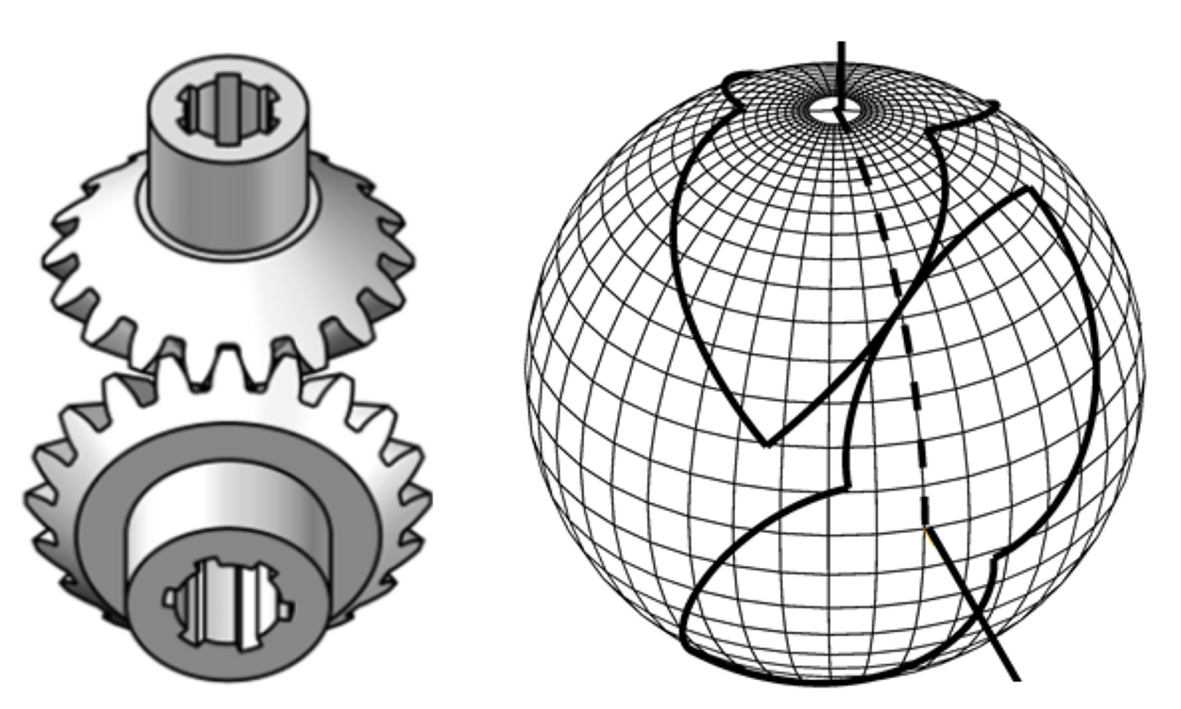
Non-circular wheels are understood as a pair of closed curves that rotate around fixed centers and at the same time roll over each other without sliding. They can serve as centroids for the design of cylindrical gears between parallel axes. If the axes of rotation of the wheels intersect, then the gears are called conical. An analog of gears between parallel axes, in which centroids are flat closed curves, for gears with intersecting axes are spherical closed curves. For a bevel gear with a constant gear ratio, such spherical curves are circles on the surface of the sphere, and with a variable gear ratio, spatial spherical curves.
This paper considers the construction of closed spherical curves that roll around each other without sliding when they rotate around the axes intersecting in the center of the spheres. These curves are formed from symmetrical arcs of the loxodrome, a curve that crosses all the meridians of the ball at a constant angle. This angle should be 45°, which ensures the intersection of the loxodrome at right angles. Analytical dependences have been derived underlying the calculations of profiles of spherical non-circular wheels and their visualization by means of computer graphics. The results could be used to design non-circular wheels for textile machines, hydraulic machine pumps, pump dispensers, etc.
References
- Konopatskiy, E., Voronova, O., Bezditnyi, A., Shevchuk, O. (2020). About one method of numeral decision of differential equalizations in partials using geometric interpolants. CPT2020 The 8th International Scientific Conference on Computing in Physics and Technology Proceedings. doi: https://doi.org/10.30987/conferencearticle_5fce27708eb353.92843700
- Konopatskiy, E. V., Bezditnyi, A. A. (2020). Geometric modeling of multifactor processes and phenomena by the multidimensional parabolic interpolation method. Journal of Physics: Conference Series, 1441 (1), 012063. doi: https://doi.org/10.1088/1742-6596/1441/1/012063
- Konopatskiy, E., Bezditnyi, A., Shevchuk, O. (2020). Modeling Geometric Varieties with Given Differential Characteristics and Its Application. Proceedings of the 30th International Conference on Computer Graphics and Machine Vision (GraphiCon 2020). Part 2, short31-1-short31-8. doi: https://doi.org/10.51130/graphicon-2020-2-4-31
- Tarelnyk, V., Martsynkovskyy, V., Gaponova, O., Konoplianchenko, I., Dovzyk, M., Tarelnyk, N., Gorovoy, S. (2017). New sulphiding method for steel and cast iron parts. IOP Conference Series: Materials Science and Engineering, 233, 012049. doi: https://doi.org/10.1088/1757-899x/233/1/012049
- Tarelnyk, V., Martsynkovskyy, V., Gaponova, O., Konoplianchenko, I., Belous, A., Gerasimenko, V., Zakharov, M. (2017). New method for strengthening surfaces of heat treated steel parts. IOP Conference Series: Materials Science and Engineering, 233, 012048. doi: https://doi.org/10.1088/1757-899x/233/1/012048
- Tarel’nik, V. B., Martsinkovskii, V. S., Zhukov, A. N. (2017). Increase in the Reliability and Durability of Metal Impulse End Seals. Part 1. Chemical and Petroleum Engineering, 53 (1-2), 114–120. doi: https://doi.org/10.1007/s10556-017-0305-y
- Pylypaka, S. F., Klendii, M. B., Trokhaniak, V. I., Kresan, T. A., Hryshchenko, I. Y., Pastushenko, A. S. (2021). External rolling of a polygon on closed curvilinear profile. Acta Polytechnica, 61 (1), 270–278. doi: https://doi.org/10.14311/ap.2021.61.0270
- Lyashkov, A. A., Panchuk, K. L., Khasanova, I. A. (2018). Automated Geometric and Computer-aided Non-Circular Gear Formation Modeling. Journal of Physics: Conference Series, 1050, 012049. doi: https://doi.org/10.1088/1742-6596/1050/1/012049
- Lyashkov, A. A., Reinhard, A. J., Murashev, G. E. (2019). Geometric And Computer Modeling of Forming the Gear Wheels with Elliptical Centroid. Journal of Physics: Conference Series, 1260 (11), 112018. doi: https://doi.org/10.1088/1742-6596/1260/11/112018
- Lin, C., Wu, X. (2018). Calculation and Characteristic Analysis of Tooth Width of Eccentric Helical Curve-Face Gear. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 43 (4), 781–797. doi: https://doi.org/10.1007/s40997-018-0239-9
- Liu, J.-G., Tong, Z.-P., Yu, G.-H., Zhao, X., Zhou, H.-L. (2022). Design and Application of Non-Circular Gear with Cusp Pitch Curve. Machines, 10 (11), 985. doi: https://doi.org/10.3390/machines10110985
- Bogdan-Roth, M., Romanet, M., Ripeanu, R. G. (2019). Device for machining non-circular gears. Proceedings on Engineering Sciences, 1 (1), 449–453. doi: https://doi.org/10.24874/pes01.01.059
- Kalchenko, V., Kalchenko, V., Kolohoida, A., Yeroshenko, A., Kalchenko, D. (2022). Building a model of dressing the working surfaces of wheels during the two-side grinding of round end faces at CNC machines. Eastern-European Journal of Enterprise Technologies, 1 (1 (115)), 86–93. doi: https://doi.org/10.15587/1729-4061.2022.252642
- Krawiec, P., Czarnecka-Komorowska, D., Warguła, Ł., Wojciechowski, S. (2021). Geometric Specification of Non-Circular Pulleys Made with Various Additive Manufacturing Techniques. Materials, 14 (7), 1682. doi: https://doi.org/10.3390/ma14071682
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Tetiana Kresan, Ali Kadhim Ahmed, Serhii Pylypaka, Tatiana Volina, Svіtlana Semirnenko, Viktor Trokhaniak, Irina Zakharova

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









