Construction of a homogeneous solution to the elasticity theory problem for an inhomogeneous truncated transversally isotropic cone

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.274300

Keywords:

inhomogeneous transversal-isotropic truncated cone, homogeneous solutions, opening angle, median surface, boundary layer

Abstract

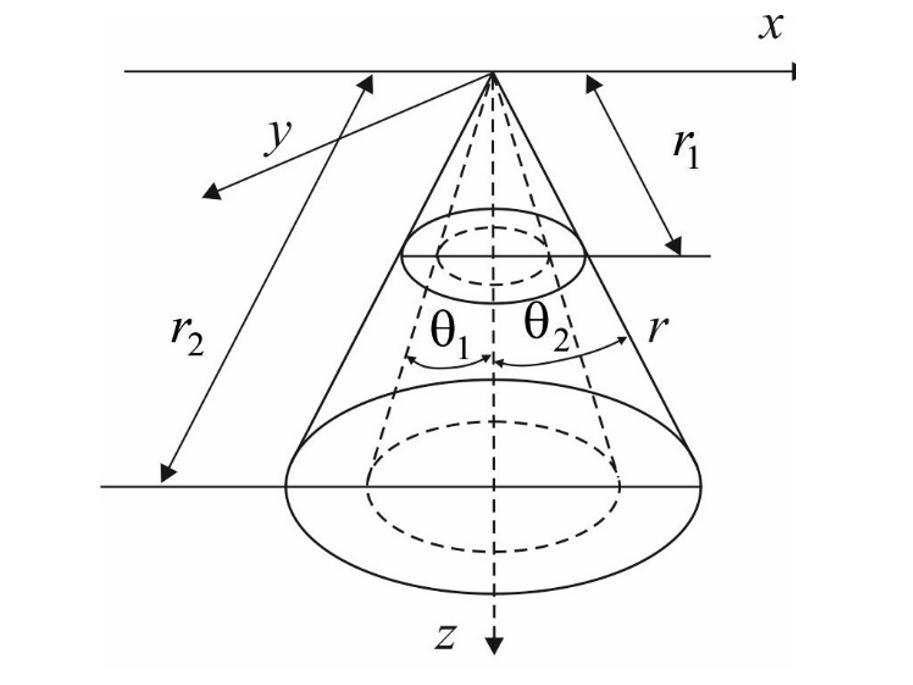
Using an asymptotic integration method, this paper investigates the axisymmetric problem of elasticity theory for an inhomogeneous transversal-isotropic truncated cone of small thickness. It is believed that the moduli of elasticity are arbitrary continuous functions of the cone opening angle. It is assumed that the lateral part of the cone is free of stresses, and arbitrary boundary conditions are set at the ends of the cone, leaving it in equilibrium. Homogeneous solutions have been constructed, that is, all solutions to equilibrium equations that satisfy the condition of absence of stresses on the lateral surfaces of the cone. Three groups of solutions were derived: a penetrating solution, solutions such as a simple edge effect, as well as the boundary layer solutions. An analysis of the stressed-strained state was carried out. It is shown that the penetrating solution and solutions having the character of a boundary effect determine the internal stressed-strained state of the cone. Solutions having the character of a boundary layer are localized at the ends of the cone and its first terms are equivalent to the edge effect of the Saint-Venant inhomogeneous plate.

A particular type of inhomogeneous transversal-isotropic cone of small thickness with the degeneration of its median surface into a plane has been studied. It is shown that this case of degeneration is special, and the solutions consist of a penetrating solution and a solution of the nature of the boundary layer.

Asymptotic formulas have been derived that make it possible to calculate the stressed-strained state of an inhomogeneous transversal-isotropic cone of small thickness. On the basis of the obtained solutions, it is possible to build a new refined applied theory and determine the applicability of existing applied theories for conical shells. New classes of solutions have been identified that no applied theory can describe

Author Biography

Natiq Akhmedov, Azerbaijan State Economic University (UNEC)

Doctor of Mathematics, Professor, Head of Department

Department of Mathematics and Statistics

References

  1. Ulitko, A. F. (2002). The vectors’ expansion in the space elasticity theory. Kyiv: Akademperiodika.
  2. Vaisfel’d, N. D., Popov, G. Ya. (2014). Torsion of a Truncated Conically Layered Elastic Cone. Journal of Mathematical Sciences, 203 (1), 134–148. doi: https://doi.org/10.1007/s10958-014-2096-4
  3. Thompson, T. R., Little, R. W. (1970). End effects in a truncated semi-infinite cone. The Quarterly Journal of Mechanics and Applied Mathematics, 23 (2), 185–196. doi: https://doi.org/10.1093/qjmam/23.2.185
  4. Khomasudridze, N. G. (2003). The thermoelastic equilibrium of conical bodies. Journal of Applied Mathematics and Mechanics, 67 (1), 111–120. doi: https://doi.org/10.1016/s0021-8928(03)80001-1
  5. Popov, G. Ya. (2005). Axisymmetric problems of the theory of elasticity for a truncated hollow cone. Journal of Applied Mathematics and Mechanics, 69 (3), 417–426. doi: https://doi.org/10.1016/j.jappmathmech.2005.05.009
  6. Vaysfel'd, N. D., Reut, A. V. (2013). Osesimmetrichnaya smeshannaya zadacha teorii uprugosti dlya pologo dvazhdy usechennogo konusa. Vestnik Kievskogo natsional'nogo universiteta, 3, 93–97.
  7. Mysov, K. D., Vaysfeld, N. D. (2018). Steady state torsion of twice truncated elastic cone. Young Scientist, 10 (1), 119–122. Available at: http://nbuv.gov.ua/UJRN/molv_2018_10%281%29__29
  8. Nuller, B. M. (1967). K resheniyu zadachi teorii uprugosti ob usechennom konuse. Izvestiya AN SSSR, Mekhanika tverdogo tela, 5, 102–110.
  9. Mekhtiev, M. F., Ustinov, Yu. A. (1970). Asimptoticheskoe povedenie resheniya osesimmetrichnoy zadachi teorii uprugosti dlya pologo konusa. Trudy 7-y Vsesoyuznoy konferentsii po teorii obolochek i plastinok. Dnepropetrovsk, 425–427.
  10. Mekhtiev, M. F., Ustinov, Yu. A. (1971). Asimptoticheskoe issledovanie resheniya zadachi teorii uprugosti dlya pologo konusa. Prikladnaya matematika i mekhanika, 35 (6), 1108–1115.
  11. Mekhtiev, M. F., Salmanov, V. S. (1985). Ravnovesie uprugogo pologo konusa s zakreplennoy bokovoy poverkhnost'yu. Izvestiya AN Azerb. SSR, Seriya fiz.-tekhn. i matem. nauk., 5, 144–147.
  12. Mekhtiev, M. F. (2018). Vibrations of hollow elastic bodies. Springer, 212. doi: https://doi.org/10.1007/978-3-319-74354-7
  13. Mekhtiev, M. F. (2019). Asymptotic analysis of spatial problems in elasticity. Springer, 241. doi: https://doi.org/10.1007/978-981-13-3062-9
  14. Akhmedov, N. K., Mekhtiev, M. F. (1993). Analiz trekhmernoy zadachi teorii uprugosti dlya neodnorodnogo usechennogo pologo konusa. Prikladnaya matematika i mekhanika, 57 (5), 113–119.
  15. Akhmedov, N. K. (1994). Kruchenie neodnorodnogo pologo konusa maloy tolschiny. Prikladnaya mekhanika, 30 (3), 62–66.
  16. Akhmedov, N. K., Shirinov, T. V. (2002). Asymptotic analysis of a space problem of elasticity theory for nonhomogeneous hollow cone of small thickness. Transactions of NAS of Azerbaijan, XXII (4), 197–203. Available at: https://transmech.imm.az/old/volume/old_volume/cild22_N4_2002/meqaleler/197-203.pdf
  17. Mekhtiev, M. F., Sardarova, N. A., Fomina, N. I. (2003). Asimptoticheskoe povedenie resheniya osesimmetrichnoy zadachi teorii uprugosti dlya transversal'no-izotropnogo pologo konusa. Izvestiya RAN, Mekhanika tverdogo tela, 2, 61–70.
  18. Mekhtiev, M. F., Ustinov, Yu. A. (1971). Asimptoticheskoe povedenie resheniya zadachi teorii uprugosti dlya plity peremennoy tolschiny. Trudy 8-y Vsesoyuznoy konferentsii po teorii obolochek i plastinok. Rostov-na Donu.
  19. Akhmedov, N. K., Mekhtiev, M. F. (1995). Osesimmetrichnaya zadacha teorii uprugosti dlya neodnorodnoy plity peremennoy tolschiny. Prikladnaya matematika i mekhanika, 59 (3), 518–7523.
  20. Mekhtiev, M. F., Amrakhova, A. R. (2003). Zadacha izgiba dlya transtropnoy plity peremennoy tolschiny. Trudy III Vserossiyskiy konferentsii po teorii upru gosti. Rostov-na-Donu.
  21. Mekhtiev, M. F., Mardanov, I. D., Amrahova, R. A. (2002). Asymptotic analysis of bending problem for transversal-isotropic plate of variable thickness. Transactions of NAS of Azerbaijan, physical-technical and mathematical sciences, 4, 223–236.
  22. Mekhtiev, M. F. (2006). Construction of homogeneous solutions of a non-axially-symmetric tension problem of elasticity theory for transversely isotropic plates of variable thickness. Transactions of NAS of Azerbaijan, physical-technical and mathematical sciences, XXVI (1), 177–186.
  23. Lur'e, A. I. (1970). Teoriya uprugosti. Moscow: Nauka.
  24. Gol'denveyzer, A. L. (1963). Postroenie priblizhennoy teorii izgiba obolochki pri pomoschi asimptoticheskogo integrirovaniya uravneniy teorii uprugosti. Prikladnaya matematika i mekhanika, 27 (4), 593–608.
  25. Akhmedov, N. K., Sofiyev, A. H. (2019). Asymptotic analysis of three-dimensional problem of elasticity theory for radially inhomogeneous transversally-isotropic thin hollow spheres. Thin-Walled Structures, 139, 232–241. doi: https://doi.org/10.1016/j.tws.2019.03.022
  26. Akhmedov, N., Akbarova, S., Ismayilova, J. (2019). Analysis of axisymmetric problem from the theory of elasticity for an isotropic cylinder of small thickness with alternating elasticity modules. Eastern-European Journal of Enterprise Technologies, 2 (7 (98)), 13–19. doi: https://doi.org/10.15587/1729-4061.2019.162153
  27. Akhmedov, N., Akbarova, S. (2021). Behavior of solution of the elasticity problem for a radial inhomogeneous cylinder with small thickness. Eastern-European Journal of Enterprise Technologies, 6 (7 (114)), 29–42. doi: https://doi.org/10.15587/1729-4061.2021.247500
  28. Ustinov, Yu. A. (2006). Matematicheskaya teoriya poperechno-neodnorodnykh plit. Rostov-na Donu.
Construction of a homogeneous solution to the elasticity theory problem for an inhomogeneous truncated transversally isotropic cone

Downloads

Published

2023-02-28

How to Cite

Akhmedov, N. (2023). Construction of a homogeneous solution to the elasticity theory problem for an inhomogeneous truncated transversally isotropic cone. Eastern-European Journal of Enterprise Technologies, 1(7 (121), 21–31. https://doi.org/10.15587/1729-4061.2023.274300

Issue

Vol. 1 No. 7 (121) (2023): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2023 Natiq Akhmedov

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.