Побудова однорідного розв'язання задачі теорії пружності для неоднорідного усіченого трансверсально-ізотропного конуса

Автор(и)

DOI:

https://doi.org/10.15587/1729-4061.2023.274300

Ключові слова:

неоднорідний трансверсально-ізотропний конус, однорідні рішення, кут розчину, серединна поверхня, прикордонний шар

Анотація

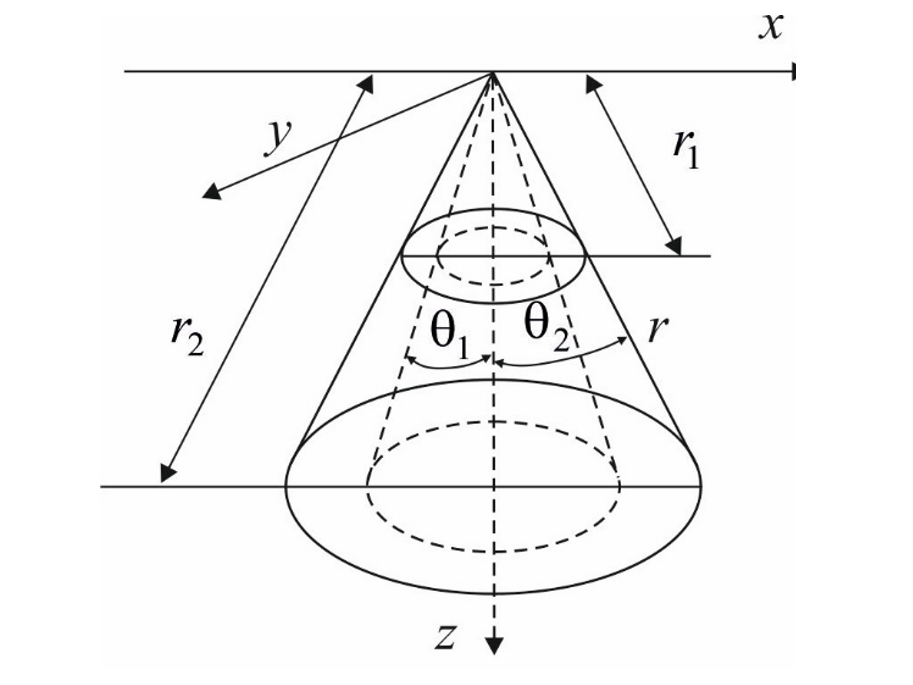
За допомогою методу асимптотичного інтегрування вивчається вісесиметрична задача теорії пружності для неоднорідного трансверсально-ізотропного зрізаного конуса малої товщини. Вважається, що модулями пружності є безперервні довільні функції від кута розчину конуса. Передбачається, що бічна частина конуса вільна від напруги, а на торцях конуса задані довільні граничні умови, що залишають її в рівновазі. Побудовано однорідні розв'язки, тобто всякі розв'язки рівнянь рівноваги, що задовольняють умову відсутності напруги на бічних поверхнях конуса. Отримано три групи рішень: проникаюче рішення, рішення типу простого крайового ефекту та рішення прикордонного шару. Проведено аналіз напружено-деформованого стану. Показано, що проникаюче рішення та рішення, що мають характер крайового ефекту, визначають внутрішній напружено-деформований стан конуса. Рішення, що мають характер прикордонного шару, локалізовані у торців конуса та його перші члени еквівалентні крайовому ефекту Сен-Венана неоднорідної плити.

Вивчено окремий вид неоднорідного трансверсально-ізотропного конуса малої товщини при виродженні її серединної поверхні в площину. Показано, що цей випадок виродження особливий і рішення складаються з проникаючого рішення та характеру прикордонного шару.

Отримано асимптотичні формули, що дозволяють розрахувати напружено-деформований стан неоднорідного трансверсально-ізотропного конуса малої товщини. На основі отриманих рішень можна побудувати нову уточнену прикладну теорію та визначити області застосування існуючих прикладних теорій для конічних оболонок. Визначено нові класи рішень, які не може описати жодна прикладна теорія

Біографія автора

Natiq Akhmedov, Azerbaijan State Economic University (UNEC)

Doctor of Mathematics, Professor, Head of Department

Department of Mathematics and Statistics

Посилання

  1. Ulitko, A. F. (2002). The vectors’ expansion in the space elasticity theory. Kyiv: Akademperiodika.
  2. Vaisfel’d, N. D., Popov, G. Ya. (2014). Torsion of a Truncated Conically Layered Elastic Cone. Journal of Mathematical Sciences, 203 (1), 134–148. doi: https://doi.org/10.1007/s10958-014-2096-4
  3. Thompson, T. R., Little, R. W. (1970). End effects in a truncated semi-infinite cone. The Quarterly Journal of Mechanics and Applied Mathematics, 23 (2), 185–196. doi: https://doi.org/10.1093/qjmam/23.2.185
  4. Khomasudridze, N. G. (2003). The thermoelastic equilibrium of conical bodies. Journal of Applied Mathematics and Mechanics, 67 (1), 111–120. doi: https://doi.org/10.1016/s0021-8928(03)80001-1
  5. Popov, G. Ya. (2005). Axisymmetric problems of the theory of elasticity for a truncated hollow cone. Journal of Applied Mathematics and Mechanics, 69 (3), 417–426. doi: https://doi.org/10.1016/j.jappmathmech.2005.05.009
  6. Vaysfel'd, N. D., Reut, A. V. (2013). Osesimmetrichnaya smeshannaya zadacha teorii uprugosti dlya pologo dvazhdy usechennogo konusa. Vestnik Kievskogo natsional'nogo universiteta, 3, 93–97.
  7. Mysov, K. D., Vaysfeld, N. D. (2018). Steady state torsion of twice truncated elastic cone. Young Scientist, 10 (1), 119–122. Available at: http://nbuv.gov.ua/UJRN/molv_2018_10%281%29__29
  8. Nuller, B. M. (1967). K resheniyu zadachi teorii uprugosti ob usechennom konuse. Izvestiya AN SSSR, Mekhanika tverdogo tela, 5, 102–110.
  9. Mekhtiev, M. F., Ustinov, Yu. A. (1970). Asimptoticheskoe povedenie resheniya osesimmetrichnoy zadachi teorii uprugosti dlya pologo konusa. Trudy 7-y Vsesoyuznoy konferentsii po teorii obolochek i plastinok. Dnepropetrovsk, 425–427.
  10. Mekhtiev, M. F., Ustinov, Yu. A. (1971). Asimptoticheskoe issledovanie resheniya zadachi teorii uprugosti dlya pologo konusa. Prikladnaya matematika i mekhanika, 35 (6), 1108–1115.
  11. Mekhtiev, M. F., Salmanov, V. S. (1985). Ravnovesie uprugogo pologo konusa s zakreplennoy bokovoy poverkhnost'yu. Izvestiya AN Azerb. SSR, Seriya fiz.-tekhn. i matem. nauk., 5, 144–147.
  12. Mekhtiev, M. F. (2018). Vibrations of hollow elastic bodies. Springer, 212. doi: https://doi.org/10.1007/978-3-319-74354-7
  13. Mekhtiev, M. F. (2019). Asymptotic analysis of spatial problems in elasticity. Springer, 241. doi: https://doi.org/10.1007/978-981-13-3062-9
  14. Akhmedov, N. K., Mekhtiev, M. F. (1993). Analiz trekhmernoy zadachi teorii uprugosti dlya neodnorodnogo usechennogo pologo konusa. Prikladnaya matematika i mekhanika, 57 (5), 113–119.
  15. Akhmedov, N. K. (1994). Kruchenie neodnorodnogo pologo konusa maloy tolschiny. Prikladnaya mekhanika, 30 (3), 62–66.
  16. Akhmedov, N. K., Shirinov, T. V. (2002). Asymptotic analysis of a space problem of elasticity theory for nonhomogeneous hollow cone of small thickness. Transactions of NAS of Azerbaijan, XXII (4), 197–203. Available at: https://transmech.imm.az/old/volume/old_volume/cild22_N4_2002/meqaleler/197-203.pdf
  17. Mekhtiev, M. F., Sardarova, N. A., Fomina, N. I. (2003). Asimptoticheskoe povedenie resheniya osesimmetrichnoy zadachi teorii uprugosti dlya transversal'no-izotropnogo pologo konusa. Izvestiya RAN, Mekhanika tverdogo tela, 2, 61–70.
  18. Mekhtiev, M. F., Ustinov, Yu. A. (1971). Asimptoticheskoe povedenie resheniya zadachi teorii uprugosti dlya plity peremennoy tolschiny. Trudy 8-y Vsesoyuznoy konferentsii po teorii obolochek i plastinok. Rostov-na Donu.
  19. Akhmedov, N. K., Mekhtiev, M. F. (1995). Osesimmetrichnaya zadacha teorii uprugosti dlya neodnorodnoy plity peremennoy tolschiny. Prikladnaya matematika i mekhanika, 59 (3), 518–7523.
  20. Mekhtiev, M. F., Amrakhova, A. R. (2003). Zadacha izgiba dlya transtropnoy plity peremennoy tolschiny. Trudy III Vserossiyskiy konferentsii po teorii upru gosti. Rostov-na-Donu.
  21. Mekhtiev, M. F., Mardanov, I. D., Amrahova, R. A. (2002). Asymptotic analysis of bending problem for transversal-isotropic plate of variable thickness. Transactions of NAS of Azerbaijan, physical-technical and mathematical sciences, 4, 223–236.
  22. Mekhtiev, M. F. (2006). Construction of homogeneous solutions of a non-axially-symmetric tension problem of elasticity theory for transversely isotropic plates of variable thickness. Transactions of NAS of Azerbaijan, physical-technical and mathematical sciences, XXVI (1), 177–186.
  23. Lur'e, A. I. (1970). Teoriya uprugosti. Moscow: Nauka.
  24. Gol'denveyzer, A. L. (1963). Postroenie priblizhennoy teorii izgiba obolochki pri pomoschi asimptoticheskogo integrirovaniya uravneniy teorii uprugosti. Prikladnaya matematika i mekhanika, 27 (4), 593–608.
  25. Akhmedov, N. K., Sofiyev, A. H. (2019). Asymptotic analysis of three-dimensional problem of elasticity theory for radially inhomogeneous transversally-isotropic thin hollow spheres. Thin-Walled Structures, 139, 232–241. doi: https://doi.org/10.1016/j.tws.2019.03.022
  26. Akhmedov, N., Akbarova, S., Ismayilova, J. (2019). Analysis of axisymmetric problem from the theory of elasticity for an isotropic cylinder of small thickness with alternating elasticity modules. Eastern-European Journal of Enterprise Technologies, 2 (7 (98)), 13–19. doi: https://doi.org/10.15587/1729-4061.2019.162153
  27. Akhmedov, N., Akbarova, S. (2021). Behavior of solution of the elasticity problem for a radial inhomogeneous cylinder with small thickness. Eastern-European Journal of Enterprise Technologies, 6 (7 (114)), 29–42. doi: https://doi.org/10.15587/1729-4061.2021.247500
  28. Ustinov, Yu. A. (2006). Matematicheskaya teoriya poperechno-neodnorodnykh plit. Rostov-na Donu.
Побудова однорідного розв'язання задачі теорії пружності для неоднорідного усіченого трансверсально-ізотропного конуса

##submission.downloads##

Опубліковано

2023-02-28

Як цитувати

Akhmedov, N. (2023). Побудова однорідного розв’язання задачі теорії пружності для неоднорідного усіченого трансверсально-ізотропного конуса. Eastern-European Journal of Enterprise Technologies, 1(7 (121), 21–31. https://doi.org/10.15587/1729-4061.2023.274300

Номер

Том 1 № 7 (121) (2023): Прикладна механіка

Розділ

Прикладна механіка

Ліцензія

Авторське право (c) 2023 Natiq Akhmedov

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.