LQR controller design for stabilization of non-linear DIP system based on ABC algorithm

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.275657

Keywords:

double inverted pendulum (DIP), non-linear systems, unstable systems, linear quadratic regulator (LQR) controller, artificial bee colony (ABC)

Abstract

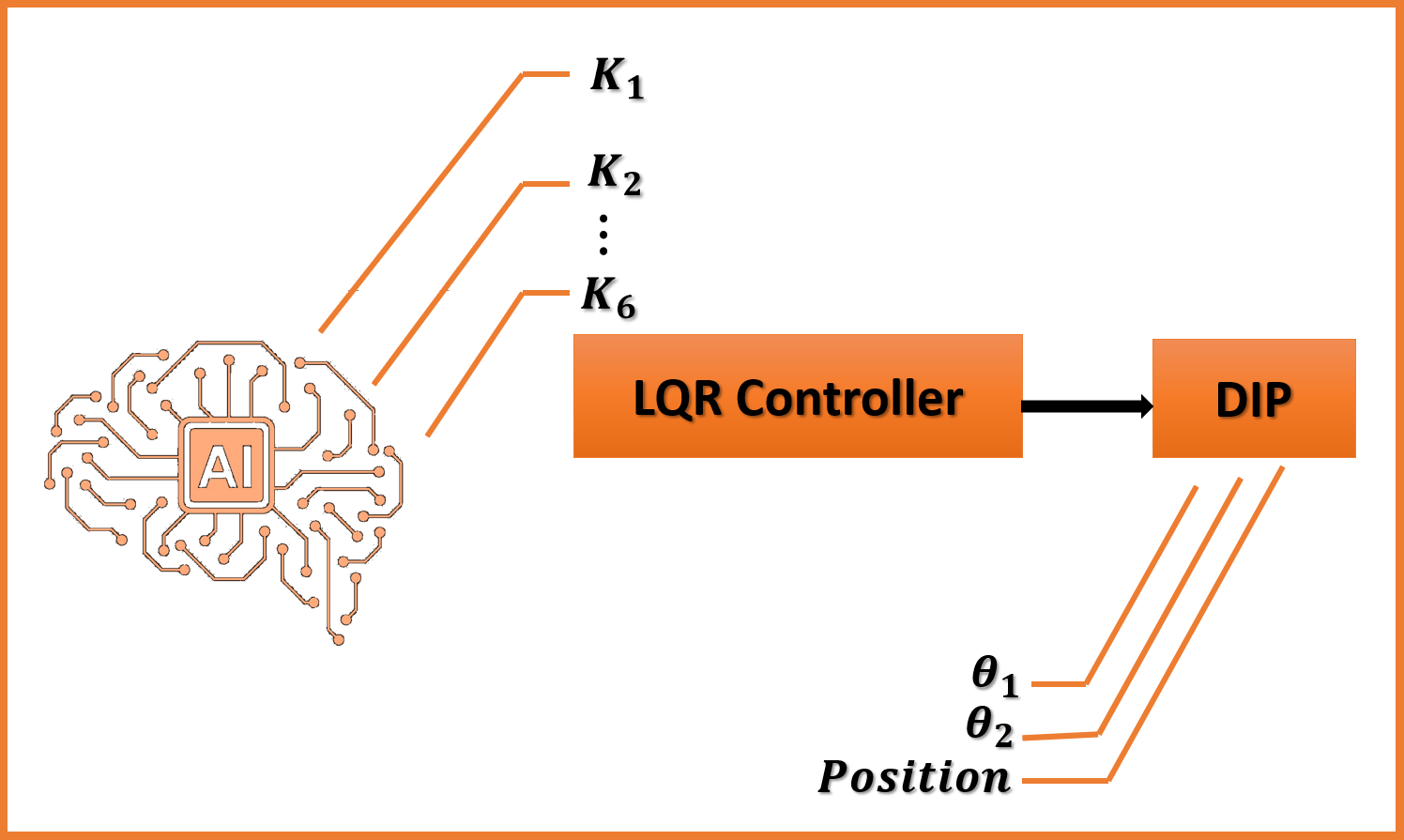
Inverted pendulum systems, such as double or single, rotational or translational inverted pendulums are non-linear and unstable, which have been the most dominant approaches for control systems. The double inverted pendulum is one kind of a non-linear, unstable system, multivariable, and strong coupling with a wide range of control methods. To model these types of systems, many techniques have been proposed so that motivating researchers to come up with new innovative solutions. The Linear Quadratic Regulator (LQR) controller has been a common controller used in this field. Meanwhile, the Artificial Bee Colony (ABC) technique has become an alternative solution for employing Bee Swarm Intelligence algorithms. The research solutions of the artificial bee colony algorithm in the literature can be beneficial, however, the utilization of discovered sources of food is ineffective. Thus, in this paper, we aim to provide a double inverted pendulum system for stabilization by selecting linear quadratic regulator parameters using a bio-inspired optimization methodology of artificial bee colony and weight matrices Q and R. The results show that when the artificial bee colony algorithm is applied to a linear quadratic regulator controller, it gains the capacity to autonomously tune itself in an online process. To further demonstrate the efficiency and viability of the suggested methodology, simulations have been performed and compared to conventional linear quadratic regulator controllers. The obtained results demonstrate that employing artificial intelligence (AI) together with the proposed controller outperforms the conventional linear quadratic regulator controllers by more than 50 % in transient response and improved time response and stability performance

Supporting Agency

  • The researchers would like to extend their thanks and appreciation to Ninevah University/College of Electronics Engineering for their support, which has assisted to boost the outcomes of this research paper.

Author Biographies

Mohammad A. Thanoon, Ninevah University

Master of Science in Computer Engineering, Assistant Lecturer

Department of Systems and Control Engineering

College of Electronics Engineering

Sohaib R. Awad, Ninevah University

Master of Science in Computer Engineering, Lecturer

Department of Computer and Information Engineering

College of Electronics Engineering

Ismael Kh. Abdullah, Ninevah University

Master of Mechanical Engineering, Assistant Lecturer

Department of Systems and Control Engineering

College of Electronics Engineering

References

  1. Łukowska, A., Tomaszuk, P., Dzierżek, K., Kamieński, K., Rólkowski, P., Ostaszewski, M. (2019). Optimal design of the double inverted pendulum. Engineering Mechanics. doi: https://doi.org/10.21495/71-0-235
  2. Susanto, E., Surya Wibowo, A., Ghiffary Rachman, E. (2020). Fuzzy Swing Up Control and Optimal State Feedback Stabilization for Self-Erecting Inverted Pendulum. IEEE Access, 8, 6496–6504. doi: https://doi.org/10.1109/access.2019.2963399
  3. Lukowska, A., Tomaszuk, P., Ciezkowski, M., Dzierzek, K., Recko, M. (2018). Acceleration control approach of double inverted pendulum system. 2018 19th International Carpathian Control Conference (ICCC). doi: https://doi.org/10.1109/carpathiancc.2018.8399614
  4. Tiunov, I. V., Vasilyev, N. O. (2021). The Modification of the ABC Synthesis Algorithm for FPGAs Considering Architecture Features. 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus). doi: https://doi.org/10.1109/elconrus51938.2021.9396324
  5. Le Dinh, L., Vo Ngoc, D., Vasant, P. (2013). Artificial Bee Colony Algorithm for Solving Optimal Power Flow Problem. The Scientific World Journal, 2013, 1–9. doi: https://doi.org/10.1155/2013/159040
  6. Xu, Y., Fan, P., Yuan, L. (2013). A Simple and Efficient Artificial Bee Colony Algorithm. Mathematical Problems in Engineering, 2013, 1–9. doi: https://doi.org/10.1155/2013/526315
  7. Banerjee, R., Dey, N., Mondal, U., Hazra, B. (2018). Stabilization of Double Link Inverted Pendulum Using LQR. 2018 International Conference on Current Trends towards Converging Technologies (ICCTCT). doi: https://doi.org/10.1109/icctct.2018.8550915
  8. Sowjanya, R., Ramesh, G. (2015). Design of optimal controller for double inverted pendulum. International Journal of Emerging Engineering Science and Technology, 1 (5), 261.
  9. Sanjeewa, S. D. A., Parnichkun, M. (2021). Control of rotary double inverted pendulum system using LQR sliding surface based sliding mode controller. Journal of Control and Decision, 9 (1), 89–101. doi: https://doi.org/10.1080/23307706.2021.1914758
  10. Zheng, Y., Zhong, P., Yue, Q. (2016). Double Inverted Pendulum Based on LQG Optimal Control. Proceedings of the 2016 International Conference on Automatic Control and Information Engineering. doi: https://doi.org/10.2991/icacie-16.2016.20
  11. Sanjeewa, S. D., Parnichkun, M. (2019). Control of rotary double inverted pendulum system using mixed sensitivity H∞ controller. International Journal of Advanced Robotic Systems, 16 (2), 172988141983327. doi: https://doi.org/10.1177/1729881419833273
  12. Singh, N., Bhangal, K. (2017). Robust Control of Double Inverted Pendulum System. Journal of Automation and Control Engineering, 5 (1), 14–20. doi: https://doi.org/10.18178/joace.5.1.14-20
  13. Jibril, M. (2020). Robust Control Theory Based Performance Investigation of an Inverted Pendulum System using Simulink. Control Theory and Informatics. doi: https://doi.org/10.7176/cti/9-04
  14. Al-Janan, D. H., Chang, H.-C., Chen, Y.-P., Liu, T.-K. (2017). Optimizing the double inverted pendulum’s performance via the uniform neuro multiobjective genetic algorithm. International Journal of Automation and Computing, 14 (6), 686–695. doi: https://doi.org/10.1007/s11633-017-1069-8
  15. Wang, Z.-M., Sun, J.-J., Yue, H. (2005). Research on an inverted pendulum optimal control system based on LQR. Industrial Instrumentation and automation, 3, 6–8.
  16. Xiong, X., Wan, Z. (2010). The simulation of double inverted pendulum control based on particle swarm optimization LQR algorithm. 2010 IEEE International Conference on Software Engineering and Service Sciences. doi: https://doi.org/10.1109/icsess.2010.5552427
  17. Molnar, C. A., Balogh, T., Boussaada, I., Insperger, T. (2020). Calculation of the critical delay for the double inverted pendulum. Journal of Vibration and Control, 27 (3-4), 356–364. doi: https://doi.org/10.1177/1077546320926909
  18. Shi, H., Xu, Z., Sun, T., Wu, C. (2019). Double Inverted Pendulum System Control Based on Internal Model Principle. 2019 34rd Youth Academic Annual Conference of Chinese Association of Automation (YAC). doi: https://doi.org/10.1109/yac.2019.8787696
  19. Barya, K., Tiwari, S., Jha, R. (2010). Comparison of LQR and robust controllers for stabilizing inverted pendulum system. 2010 International Conference on Communication Control and Computing Technologies. doi: https://doi.org/10.1109/icccct.2010.5670570
  20. Habib, M. K., Ayankoso, S. A. (2020). Modeling and Control of a Double Inverted Pendulum using LQR with Parameter Optimization through GA and PSO. 2020 21st International Conference on Research and Education in Mechatronics (REM). doi: https://doi.org/10.1109/rem49740.2020.9313893
  21. Karaboga, D., Basturk, B. (2007). Artificial Bee Colony (ABC) Optimization Algorithm for Solving Constrained Optimization Problems. Foundations of Fuzzy Logic and Soft Computing, 789–798. doi: https://doi.org/10.1007/978-3-540-72950-1_77
  22. Bozogullarindan, E., Bozogullarindan, C., Ozturk, C. (2020). Transfer Learning in Artificial Bee Colony Programming. 2020 Innovations in Intelligent Systems and Applications Conference (ASYU). doi: https://doi.org/10.1109/asyu50717.2020.9259801
LQR controller design for stabilization of non-linear DIP system based on ABC algorithm

Downloads

Published

2023-04-17

How to Cite

Thanoon, M. A., Awad, S. R., & Abdullah, I. K. (2023). LQR controller design for stabilization of non-linear DIP system based on ABC algorithm . Eastern-European Journal of Enterprise Technologies, 2(2 (122), 36–44. https://doi.org/10.15587/1729-4061.2023.275657

Issue

Vol. 2 No. 2 (122) (2023): Information technology. Industry control systems

Section

Industry control systems

License

Copyright (c) 2023 Mohammad A. Thanoon, Sohaib R. Awad, Ismael Kh. Abdullah

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.