Design of mechanisms for ensuring the execution of tasks in project planning

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.277585

Keywords:

decision-making, distribution of performers, cost-time efficiency, ideal point

Abstract

This paper reports an analysis of aspects of the project planning stage. The object of research is the decision-making processes that take place at this stage. This work considers the problem of building a hierarchy of tasks, their distribution among performers, taking into account restrictions on financial costs and duration of project implementation.

Verbal and mathematical models of the task of constructing a hierarchy of tasks and other tasks that take place at the stage of project planning were constructed.

Such indicators of the project implementation process efficiency were introduced as the time, cost, and cost-time efficiency. In order to be able to apply these criteria, the tasks of estimating the minimum value of the duration of the project and its minimum required cost were considered. Appropriate methods have been developed to solve them.

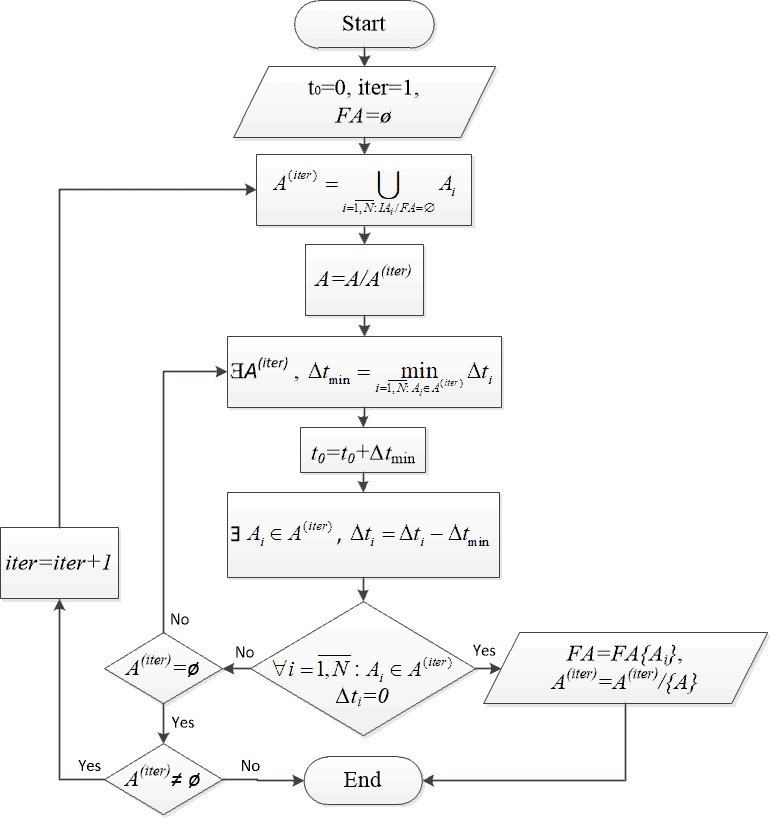
The developed iterative method for assessing the minimum duration of project implementation is based on taking into account the possibility of simultaneous execution of various tasks. The method of estimating the minimum cost of the project is to build and solve the problem of Boolean programming.

The values obtained as a result of solving these problems form an «ideal point», approaching which is enabled by the developed iterative method of constructing a hierarchy of tasks based on the method of sequential concessions. This method makes it possible to devise options for management decisions to obtain valid solutions to the problem. According to them, the decision maker can introduce a concession on the value of one or both components of the «ideal point» or change the input data to the task.

The models and methods built can be used when planning projects in education, science, production, etc.

Author Biographies

Oksana Mulesa, Uzhhorod National University

Doctor of Technical Sciences, Professor

Department of Software Systems

Petro Horvat, Uzhhorod National University

PhD, Associate Professor, Head of Department

Department of Computer Systems and Networks

Tamara Radivilova, Kharkiv National University of Radio Electronics

Doctor of Technical Sciences, Professor

V. V. Popovskyy Department of Infocommunication

Volodymyr Sabadosh, Intellias Company

Senior Java Developer

Oleksii Baranovskyi, Blekinge Institute of Technology

PhD, Senior Lecturer

Department of Computer Science

Sergii Duran, Uzhhorod National University

Postgraduate Student

Department of Software Systems

References

  1. Picciotto, R. (2020). Towards a ‘New Project Management’ movement? An international development perspective. International Journal of Project Management, 38 (8), 474–485. doi: https://doi.org/10.1016/j.ijproman.2019.08.002
  2. Chen, Z., Wang, F. (2022). Research on Life-Cycle Project Cost Management Based on Random Matrix Weight Algorithm. Mathematical Problems in Engineering, 2022, 1–12. https://doi.org/10.1155/2022/5211409
  3. Ernø-Kjølhede, E. (2000). Project management theory and the management of research projects. CBS. Available at: https://research-api.cbs.dk/ws/portalfiles/portal/58880359/6308.pdf
  4. Mulesa, O., Myronyuk, I., Kachmar, O., Jakab, F., Yatsyna, O. (2022). Decision-Making Modeling in Educational Process Organization Under the Conditions of Crisis Situations Forecasting. 2022 20th International Conference on Emerging ELearning Technologies and Applications (ICETA). doi: https://doi.org/10.1109/iceta57911.2022.9974909
  5. Lock, D. (2020). Project management. Routledge. doi: https://doi.org/10.1201/9781315245911
  6. Kerzner, H. (2019). Using the project management maturity model: strategic planning for project management. John Wiley & Sons. doi: https://doi.org/10.1002/9781119559078
  7. Peres, F., Castelli, M. (2021). Combinatorial Optimization Problems and Metaheuristics: Review, Challenges, Design, and Development. Applied Sciences, 11 (14), 6449. doi: https://doi.org/10.3390/app11146449
  8. Syan, C. S., Ramsoobag, G. (2019). Maintenance applications of multi-criteria optimization: A review. Reliability Engineering & System Safety, 190, 106520. doi: https://doi.org/10.1016/j.ress.2019.106520
  9. Hnatiienko, H. (2019). Choice Manipulation in Multicriteria Optimization Problems. Selected Papers of the XIX International Scientific and Practical Conference "Information Technologies and Security" (ITS 2019), 234–245. Available at: https://ceur-ws.org/Vol-2577/paper19.pdf
  10. Mulesa, O., Snytyuk, V., Myronyuk, I. (2019). Optimal alternative selection models in a multi-stage decision-making process. EUREKA: Physics and Engineering, 6, 43–50. doi: https://doi.org/10.21303/2461-4262.2019.001005
  11. Tsmots, I., Teslyuk, V., Teslyuk, T., Lukashchuk, Y. (2021). The Method and Simulation Model of Element Base Selection for Protection System Synthesis and Data Transmission. International Journal of Sensors, Wireless Communications and Control, 11 (5), 518–530. doi: https://doi.org/10.2174/2210327910999201022194630
  12. Verma, S., Pant, M., Snasel, V. (2021). A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access, 9, 57757–57791. doi: https://doi.org/10.1109/access.2021.3070634
  13. Vesselinova, N., Steinert, R., Perez-Ramirez, D. F., Boman, M. (2020). Learning Combinatorial Optimization on Graphs: A Survey With Applications to Networking. IEEE Access, 8, 120388–120416. doi: https://doi.org/10.1109/access.2020.3004964
  14. Hettiachchi, D., Kostakos, V., Goncalves, J. (2022). A Survey on Task Assignment in Crowdsourcing. ACM Computing Surveys, 55 (3), 1–35. doi: https://doi.org/10.1145/3494522
  15. Kumai, K., Matsubara, M., Shiraishi, Y., Wakatsuki, D., Zhang, J., Shionome, T. et al. (2018). Skill-and-Stress-Aware Assignment of Crowd-Worker Groups to Task Streams. Proceedings of the AAAI Conference on Human Computation and Crowdsourcing, 6, 88–97. doi: https://doi.org/10.1609/hcomp.v6i1.13328
  16. Bakshi, S., Feng, T., Yan, Z., Chen, D. (2019). A Regularized Quadratic Programming Approach to Real-Time Scheduling of Autonomous Mobile Robots in a Prioritized Task Space. 2019 American Control Conference (ACC). doi: https://doi.org/10.23919/acc.2019.8814986
  17. Yang, K., Wang, Y., Fan, S., Mosleh, A. (2021). Multi-Criteria Spare Parts Classification Using the Deep Convolutional Neural Network Method. Applied Sciences, 11 (15), 7088. doi: https://doi.org/10.3390/app11157088
  18. Bodnarchuk, I., Duda, O., Kharchenko, A., Kunanets, N., Matsiuk, O., Pasichnyk, V. (2019). Multicriteria Choice of Software Architecture Using Dynamic Correction of Quality Attributes. Advances in Intelligent Systems and Computing, 419–427. doi: https://doi.org/10.1007/978-3-030-16621-2_39
  19. Biloshchytskyi, A., Biloshchytska, S., Kuchansky, A., Bielova, O., Andrashko, Y. (2018). Infocommunication system of scientific activity management on the basis of project-vector methodology. 2018 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET). doi: https://doi.org/10.1109/tcset.2018.8336186
  20. Mulesa, O. (2015). Methods of considering the subjective character of input data in voting. Eastern-European Journal of Enterprise Technologies, 1 (3 (73)), 20–25. doi: https://doi.org/10.15587/1729-4061.2015.36699
  21. Mulesa, O., Geche, F. (2016). Designing fuzzy expert methods of numeric evaluation of an object for the problems of forecasting. Eastern-European Journal of Enterprise Technologies, 3 (4 (81)), 37–43. doi: https://doi.org/10.15587/1729-4061.2016.70515
  22. Tanabe, R., Ishibuchi, H. (2020). A Review of Evolutionary Multimodal Multiobjective Optimization. IEEE Transactions on Evolutionary Computation, 24 (1), 193–200. doi: https://doi.org/10.1109/tevc.2019.2909744
  23. Lin, Q., Lin, W., Zhu, Z., Gong, M., Li, J., Coello, C. A. C. (2021). Multimodal Multiobjective Evolutionary Optimization With Dual Clustering in Decision and Objective Spaces. IEEE Transactions on Evolutionary Computation, 25 (1), 130–144. doi: https://doi.org/10.1109/tevc.2020.3008822
  24. Bakurova, A., Ropalo, H., Tereschenko, E. (2021). Analysis of the Effectiveness of the Successive Concessions Method to Solve the Problem of Diversification. MoMLeT+ DS, 231–242. Available at: https://ceur-ws.org/Vol-2917/paper21.pdf
  25. Koliechkina, L. N., Dvirna, O. A., Khovben, S. V. (2021). A Two-Step Method for Solving Vector Optimization Problems on Permutation Configuration. Cybernetics and Systems Analysis, 57 (3), 442–454. doi: https://doi.org/10.1007/s10559-021-00369-3
  26. Papke-Shields, K. E., Boyer-Wright, K. M. (2017). Strategic planning characteristics applied to project management. International Journal of Project Management, 35 (2), 169–179. doi: https://doi.org/10.1016/j.ijproman.2016.10.015
  27. Globerson, S., Zwikael, O. (2002). The Impact of the Project Manager on Project Management Planning Processes. Project Management Journal, 33 (3), 58–64. doi: https://doi.org/10.1177/875697280203300308
Design of mechanisms for ensuring the execution of tasks in project planning

Downloads

Published

2023-04-29

How to Cite

Mulesa, O., Horvat, P., Radivilova, T., Sabadosh, V., Baranovskyi, O., & Duran, S. (2023). Design of mechanisms for ensuring the execution of tasks in project planning . Eastern-European Journal of Enterprise Technologies, 2(4 (122), 16–22. https://doi.org/10.15587/1729-4061.2023.277585

Issue

Vol. 2 No. 4 (122) (2023): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2023 Oksana Mulesa, Petro Horvat, Tamara Radivilova, Volodymyr Sabadosh, Oleksii Branovskyi, Sergii Duran

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.