Determining regularities in the construction of curves and surfaces using the Darboux trihedron
DOI:
https://doi.org/10.15587/1729-4061.2023.279007Keywords:
accompanying trihedron, Darboux trihedron, parametric equations of curves and surfaces, transition formulasAbstract
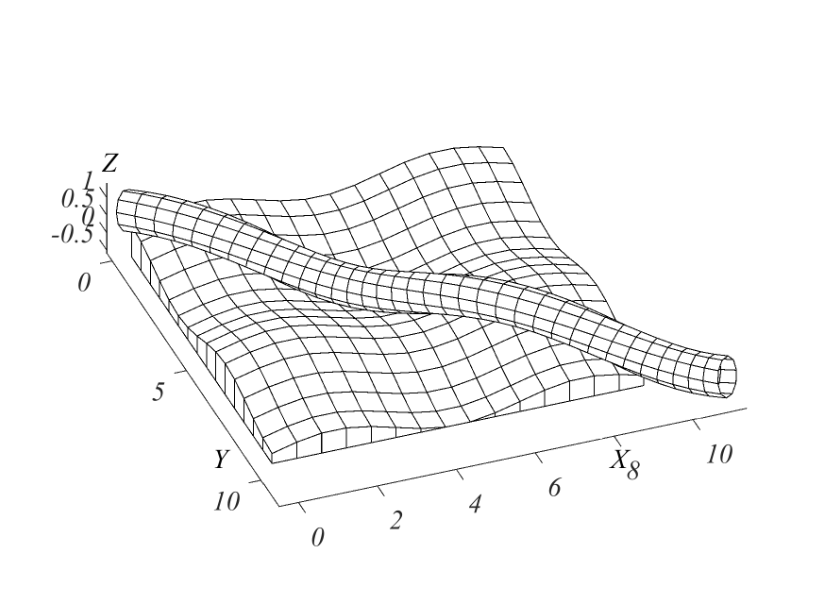
The Frénet trihedron, known in differential geometry, is accompanying for a spatial and, as a special case, for a flat curve. Its three mutually perpendicular unit orts are defined uniquely for any point on the curve except for some special ones. Unlike the Frénet trihedron, the Darboux trihedron relates to the surface. Two of its unit orts are located in a plane tangent to the surface, and the third is directed normally to the surface. It can also be accompanying for the curve, which is located on the surface. To this end, one of the orts in the plane tangent to the surface must be tangent to the curve.
Trihedra are movable and, with respect to a fixed coordinate system, change their position due to movement and rotation. The object of research is the process of formation of curves and surfaces, as a result of the geometric sum of the bulk motion of the Darboux trihedron and the relative motion of the point in its system under given conditions. In the study of the geometric characteristics of curves and surfaces, it is necessary to have formulas for the transition from the position of the elements of these objects in the system of a moving trihedron to the position in a fixed Cartesian coordinate system. This is exactly what needs to be solved. The results obtained are parametric equations of curves and surfaces that are tied to the initial surface. Nine guide cosines were found, three for each ort.
A distinctive feature of this approach in comparison with the traditional one is the use of two systems: fixed and mobile, which is the Darboux trihedron. This approach allows us to consider in a new way the problem of the construction of curves and surfaces. The scope of practical application can be the construction of geometric shapes on a given surface. An example of such a construction is the laying of a pipeline along a given line on the surface. In addition, the sum of the relative motion of a point in a trihedron and the bulk motion of the trihedron itself over the surface gives an absolute trajectory of motion. Its sequential differentiation produces absolute speed and absolute acceleration without finding individual components, including the Coriolis acceleration. This could be used in point dynamics problems
References
- Martsynkovskyy, V., Tarelnyk, V., Konoplianchenko, I., Gaponova, O., Dumanchuk, M. (2019). Technology Support for Protecting Contacting Surfaces of Half-Coupling—Shaft Press Joints Against Fretting Wear. Advances in Design, Simulation and Manufacturing II, 216–225. doi: https://doi.org/10.1007/978-3-030-22365-6_22
- Gaponova, O., Kundera, Cz., Kirik, G., Tarelnyk, V., Martsynkovskyy, V., Konoplianchenko, Ie. et al. (2019). Estimating Qualitative Parameters of Aluminized Coating Obtained by Electric Spark Alloying Method. Advances in Thin Films, Nanostructured Materials, and Coatings, 249–266. doi: https://doi.org/10.1007/978-981-13-6133-3_25
- Pogrebnjak, A. D., Bagdasaryan, A. A., Horodek, P., Tarelnyk, V., Buranich, V. V., Amekura, H. et al. (2021). Positron annihilation studies of defect structure of (TiZrHfNbV)N nitride coatings under Xe14+ 200 MeV ion irradiation. Materials Letters, 303, 130548. doi: https://doi.org/10.1016/j.matlet.2021.130548
- Tarelnyk, V., Konoplianchenko, I., Tarelnyk, N., Kozachenko, A. (2019). Modeling Technological Parameters for Producing Combined Electrospark Deposition Coatings. Materials Science Forum, 968, 131–142. doi: https://doi.org/10.4028/www.scientific.net/msf.968.131
- Konopatskiy, E., Bezditnyi, A. (2021). Solid Modeling of Geometric Objects in Point Calculus. Proceedings of the 31th International Conference on Computer Graphics and Vision. Volume 2. doi: https://doi.org/10.20948/graphicon-2021-3027-666-672
- Konopatskiy, E. V., Bezditnyi, A. A., Lagunova, M. V., Naidysh, A. V. (2021). Principles of solid modelling in point calculus. Journal of Physics: Conference Series, 1901 (1), 012063. doi: https://doi.org/10.1088/1742-6596/1901/1/012063
- Konopatskiy, E. V., Bezditnyi, A. A., Litvinov, A. I. (2021). Geometric modeling of torse surfaces in BN-calculus. Journal of Physics: Conference Series, 1791 (1), 012050. doi: https://doi.org/10.1088/1742-6596/1791/1/012050
- Gorobets, V., Trokhaniak, V., Bohdan, Yu., Antypov, Ie. (2021). Numerical modeling of heat transfer and hydrodynamics in compact shifted arrangement small diameter tube bundles. Journal of Applied and Computational Mechanics, 7 (1), 292–301. doi: doi: https://doi.org/10.22055/JACM.2020.31007.1855
- Gorobets, V., Trokhaniak, V., Masiuk, M., Spodyniuk, N., Blesnyuk, O., Marchishina, Y. (2021). CFD modeling of aerodynamic flow in a wind turbine with vertical rotational axis and wind flow concentrator. INMATEH Agricultural Engineering, 64 (2), 159–166. doi: https://doi.org/10.35633/inmateh-64-15
- Rogovskii, I. L., Titova, L. L., Trokhaniak, V. I., Borak, K. V., Lavrinenko, O. T., Bannyi, O. O. (2021). Research on a grain cultiseeder for subsoil-broadcast sowing. INMATEH Agricultural Engineering, 63 (1), 385–396. doi: https://doi.org/10.35633/inmateh-63-39
- Volina, T., Pylypaka, S., Nesvidomin, V., Pavlov, A., Dranovska, S. (2021). The possibility to apply the Frenet trihedron and formulas for the complex movement of a point on a plane with the predefined plane displacement. Eastern-European Journal of Enterprise Technologies, 3 (7 (111)), 45–50. doi: https://doi.org/10.15587/1729-4061.2021.232446
- Kresan, T. (2021). Movement of soil particles on surface of developable helicoid with horizontal axis of rotation with given angle of attack. Machinery & Energetics, 12 (2), 67–75. doi: https://doi.org/10.31548/machenergy2021.02.067
- Borysenko, V. D., Ustenko, S. A., Ustenko, I. V. (2018). Heometrychne modeliuvannia kryvykh liniy i poverkhon u naturalniy parametryzatsiyi. Mykolaiv: MNU, 216.
- Gavrilenko, E. A., Kholodnyak, Yu. V., Naydysh, A. V. (2018). Modeling of one-dimensional contours with ensure of given accuracy of interpolation. Visnyk Khersonskoho natsionalnoho tekhnichnoho universytetu, 2 (3), 125–129. Available at: http://nbuv.gov.ua/UJRN/Vkhdtu_2018_3(2)__22
- Novoe v sisteme Mathematica 13. Available at: https://www.wolfram.com/mathematica/new-in-13/?src=google&416&gclid=CjwKCAjwoIqhBhAGEiwArXT7K8zKs9Z8YovGKAWvKBp7u47bBVWpdVSzgJKfFc9pm5A6bmMfWlUH1hoCu1cQAvD_BwE
- The Essential Tool for Mathematics. Available at: https://www.maplesoft.com/products/Maple/
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Ali Kadhim Ahmed, Andrii Nesvidomin, Serhii Pylypaka, Tatiana Volina, Serhii Dieniezhnikov

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









