Визначення закономірностей утворення кривих та поверхонь за допомогою тригранника Дарбу
DOI:
https://doi.org/10.15587/1729-4061.2023.279007Ключові слова:
супровідний тригранник, тригранник Дарбу, параметричні рівняння кривих і поверхонь, формули переходуАнотація
У диференціальній геометрії відомим є тригранник Френе, який є супровідним для просторової і, як окремий випадок, для плоскої кривої. Три його взаємно перпендикулярні одиничні орти визначаються однозначно для будь-якої точки кривої за винятком деяких особливих. На відміну від тригранника Френе, тригранник Дарбу стосується поверхні. Два його одиничні орти розташовані в дотичній до поверхні площині, а третій спрямовано по нормалі до поверхні. Він теж може бути супровідним для кривої, яка розташована на поверхні. Для цього один із ортів у дотичній до поверхні площині має бути дотичним до кривої.
Тригранники є рухомими і по відношенню до нерухомої системи координат змінюють своє положення за рахунок переміщення і повороту. Об’єктом дослідження є процес утворення кривих і поверхонь, як результат геометричної суми переносного руху тригранника Дарбу і відносного руху точки у його системі за заданими умовами. При дослідженні геометричних характеристик кривих та поверхонь необхідно мати формули переходу від положення елементів цих об’єктів у системі рухомого тригранника до положення в нерухомій декартовій системі координат. Саме це є і проблемою, яку необхідно вирішити. Отриманими результатами є параметричні рівняння кривих і поверхонь, які прив’язані до вихідної поверхні. Знайдено дев’ять напрямних косинусів – по три на кожен орт.
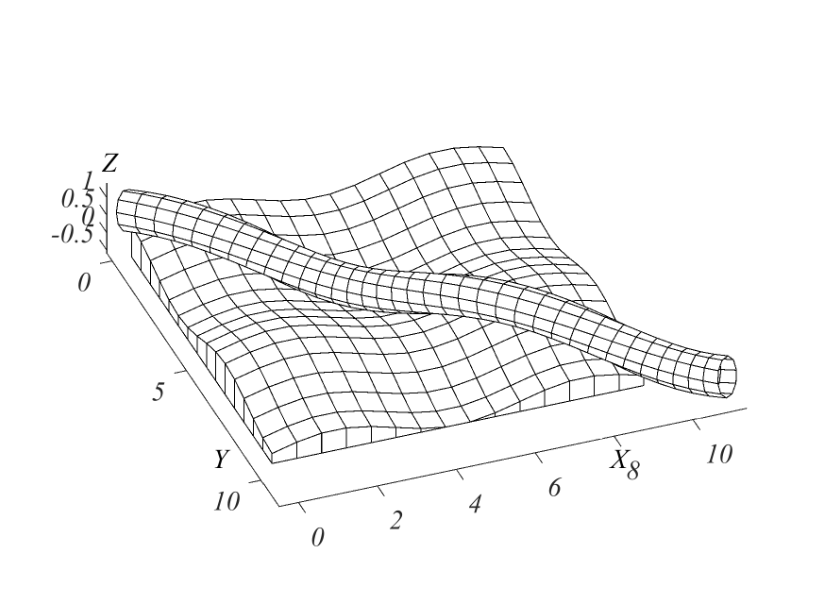
Відмінною рисою такого підходу в порівнянні з традиційним є використання двох систем: нерухомої і рухомої, якою є тригранник Дарбу. Такий підхід дозволяє по новому розглянути задачу утворення кривих і поверхонь. Сферою практичного застосування може бути побудова геометричних форм на заданій поверхні. Прикладом такої побудови є прокладання трубопроводу вздовж заданої лінії на поверхні. Крім того, сума відносного руху точки у триграннику і переносного руху самого тригранника по поверхні дає абсолютну траєкторію руху. Послідовне її диференціювання дає абсолютну швидкість і абсолютне прискорення без знаходження окремих складових, включаючи прискорення Коріоліса. Це може бути використано в задачах динаміки точки
Посилання
- Martsynkovskyy, V., Tarelnyk, V., Konoplianchenko, I., Gaponova, O., Dumanchuk, M. (2019). Technology Support for Protecting Contacting Surfaces of Half-Coupling—Shaft Press Joints Against Fretting Wear. Advances in Design, Simulation and Manufacturing II, 216–225. doi: https://doi.org/10.1007/978-3-030-22365-6_22
- Gaponova, O., Kundera, Cz., Kirik, G., Tarelnyk, V., Martsynkovskyy, V., Konoplianchenko, Ie. et al. (2019). Estimating Qualitative Parameters of Aluminized Coating Obtained by Electric Spark Alloying Method. Advances in Thin Films, Nanostructured Materials, and Coatings, 249–266. doi: https://doi.org/10.1007/978-981-13-6133-3_25
- Pogrebnjak, A. D., Bagdasaryan, A. A., Horodek, P., Tarelnyk, V., Buranich, V. V., Amekura, H. et al. (2021). Positron annihilation studies of defect structure of (TiZrHfNbV)N nitride coatings under Xe14+ 200 MeV ion irradiation. Materials Letters, 303, 130548. doi: https://doi.org/10.1016/j.matlet.2021.130548
- Tarelnyk, V., Konoplianchenko, I., Tarelnyk, N., Kozachenko, A. (2019). Modeling Technological Parameters for Producing Combined Electrospark Deposition Coatings. Materials Science Forum, 968, 131–142. doi: https://doi.org/10.4028/www.scientific.net/msf.968.131
- Konopatskiy, E., Bezditnyi, A. (2021). Solid Modeling of Geometric Objects in Point Calculus. Proceedings of the 31th International Conference on Computer Graphics and Vision. Volume 2. doi: https://doi.org/10.20948/graphicon-2021-3027-666-672
- Konopatskiy, E. V., Bezditnyi, A. A., Lagunova, M. V., Naidysh, A. V. (2021). Principles of solid modelling in point calculus. Journal of Physics: Conference Series, 1901 (1), 012063. doi: https://doi.org/10.1088/1742-6596/1901/1/012063
- Konopatskiy, E. V., Bezditnyi, A. A., Litvinov, A. I. (2021). Geometric modeling of torse surfaces in BN-calculus. Journal of Physics: Conference Series, 1791 (1), 012050. doi: https://doi.org/10.1088/1742-6596/1791/1/012050
- Gorobets, V., Trokhaniak, V., Bohdan, Yu., Antypov, Ie. (2021). Numerical modeling of heat transfer and hydrodynamics in compact shifted arrangement small diameter tube bundles. Journal of Applied and Computational Mechanics, 7 (1), 292–301. doi: doi: https://doi.org/10.22055/JACM.2020.31007.1855
- Gorobets, V., Trokhaniak, V., Masiuk, M., Spodyniuk, N., Blesnyuk, O., Marchishina, Y. (2021). CFD modeling of aerodynamic flow in a wind turbine with vertical rotational axis and wind flow concentrator. INMATEH Agricultural Engineering, 64 (2), 159–166. doi: https://doi.org/10.35633/inmateh-64-15
- Rogovskii, I. L., Titova, L. L., Trokhaniak, V. I., Borak, K. V., Lavrinenko, O. T., Bannyi, O. O. (2021). Research on a grain cultiseeder for subsoil-broadcast sowing. INMATEH Agricultural Engineering, 63 (1), 385–396. doi: https://doi.org/10.35633/inmateh-63-39
- Volina, T., Pylypaka, S., Nesvidomin, V., Pavlov, A., Dranovska, S. (2021). The possibility to apply the Frenet trihedron and formulas for the complex movement of a point on a plane with the predefined plane displacement. Eastern-European Journal of Enterprise Technologies, 3 (7 (111)), 45–50. doi: https://doi.org/10.15587/1729-4061.2021.232446
- Kresan, T. (2021). Movement of soil particles on surface of developable helicoid with horizontal axis of rotation with given angle of attack. Machinery & Energetics, 12 (2), 67–75. doi: https://doi.org/10.31548/machenergy2021.02.067
- Borysenko, V. D., Ustenko, S. A., Ustenko, I. V. (2018). Heometrychne modeliuvannia kryvykh liniy i poverkhon u naturalniy parametryzatsiyi. Mykolaiv: MNU, 216.
- Gavrilenko, E. A., Kholodnyak, Yu. V., Naydysh, A. V. (2018). Modeling of one-dimensional contours with ensure of given accuracy of interpolation. Visnyk Khersonskoho natsionalnoho tekhnichnoho universytetu, 2 (3), 125–129. Available at: http://nbuv.gov.ua/UJRN/Vkhdtu_2018_3(2)__22
- Novoe v sisteme Mathematica 13. Available at: https://www.wolfram.com/mathematica/new-in-13/?src=google&416&gclid=CjwKCAjwoIqhBhAGEiwArXT7K8zKs9Z8YovGKAWvKBp7u47bBVWpdVSzgJKfFc9pm5A6bmMfWlUH1hoCu1cQAvD_BwE
- The Essential Tool for Mathematics. Available at: https://www.maplesoft.com/products/Maple/
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2023 Ali Kadhim Ahmed, Andrii Nesvidomin, Serhii Pylypaka, Tatiana Volina, Serhii Dieniezhnikov

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









