Development of a new lightweight encryption algorithm

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.280055

Keywords:

encryption algorithm, lightweight algorithm, cryptographic transformations, avalanche effect, cryptographic stability

Abstract

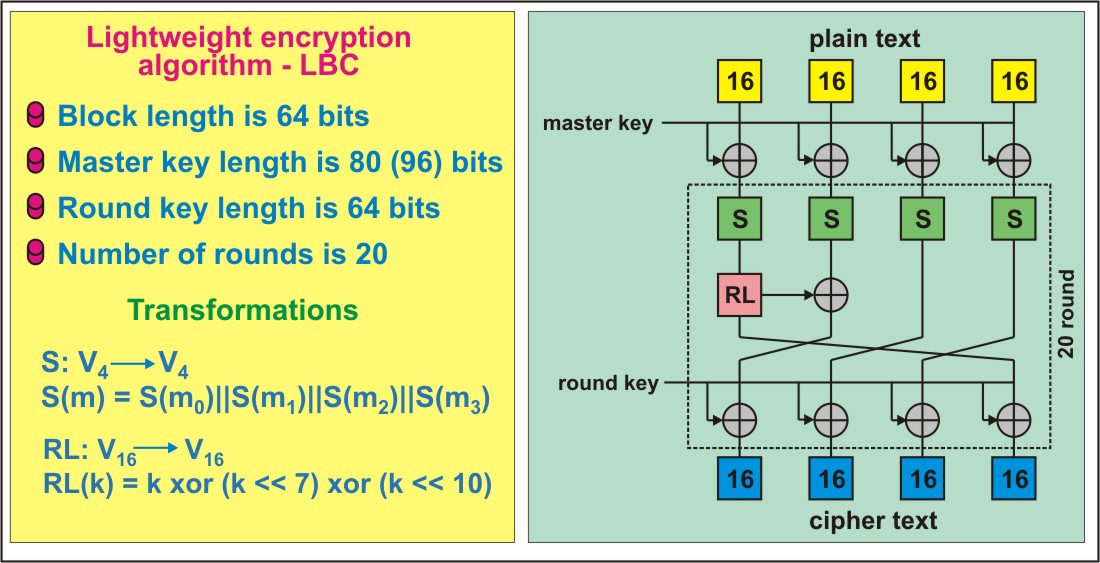
Lightweight encryption algorithms are considered a relatively new direction in the development of private key cryptography. This need arose as a result of the emergence of a large number of devices with little computing power and memory. Therefore, it became necessary to develop algorithms that can provide a sufficient level of security, with minimal use of resources. The paper presents a new lightweight LBC encryption algorithm. LBC is a 64–bit symmetric block algorithm. It supports 80 bit secret key. The number of rounds is 20. The algorithm has a Feistel network structure. The developed lightweight algorithm has a simple implementation scheme, and the transformations used in this algorithm have good cryptographic properties. This was verified by studying the cryptographic properties of the algorithm using the "avalanche effect" and statistical tests. The avalanche property was checked for each round when each bit of the source text was changed. Based on the work carried out, it was found that the proposed encryption algorithm is effective to ensure a good avalanche effect and the binary sequence obtained after encryption is close to random. Its security against linear and differential cryptanalysis is also evaluated. The results of the research revealed good cryptographic properties of this algorithm.  The algorithm will be used for devices with small hardware resources, in information and communication systems where confidential information circulates, and it is also extremely necessary to exchange information in a protected form in an operationally acceptable time

Author Biographies

Nursulu Kapalova, Institute of Information and Computational Technologies

Leading Researcher, Candidate of Technical Sciences, Associate Professor

Information Security Laboratory

Kunbolat Algazy, Institute of Information and Computational Technologies

Senior Researcher, PhD

Information Security Laboratory

Armanbek Haumen, Institute of Information and Computational Technologies

Research Associate

Information Security Laboratory

References

  1. Usman, M., Ahmed, I., Imran, M., Khan, S., Ali, U. (2017). SIT: A Lightweight Encryption Algorithm for Secure Internet of Things. International Journal of Advanced Computer Science and Applications, 8 (1). doi: https://doi.org/10.14569/ijacsa.2017.080151
  2. Yun, J., Kim, M. (2020). JLVEA: Lightweight Real-Time Video Stream Encryption Algorithm for Internet of Things. Sensors, 20 (13), 3627. doi: https://doi.org/10.3390/s20133627
  3. Taresh, H. (2018). LT10 a lightweight proposed encryption algorithm for IOT. Iraqi Journal for Computers and Informatics, 44 (1), 1–5. doi: https://doi.org/10.25195/ijci.v44i1.64
  4. Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S., Weeks, B., Wingers, L. (2013). Paper 2013/404. The SIMON and SPECK families of lightweight block ciphers. Cryptology ePrint Archive. Available at: https://eprint.iacr.org/2013/404
  5. Gu, D., Li, J., Li, S., Ma, Z., Guo, Z., Liu, J. (2012). Differential Fault Analysis on Lightweight Blockciphers with Statistical Cryptanalysis Techniques. 2012 Workshop on Fault Diagnosis and Tolerance in Cryptography. doi: https://doi.org/10.1109/fdtc.2012.16
  6. Kumar V G, K., Rai C, S. (2021). Design and Implementation of Novel BRISI Lightweight Cipher for Resource Constrained Devices. Microprocessors and Microsystems, 84, 104267. doi: https://doi.org/10.1016/j.micpro.2021.104267
  7. Yang, W., Wang, R., Guan, Z., Wu, L., Du, X., Guizani, M. (2020). A Lightweight Attribute Based Encryption Scheme with Constant Size Ciphertext for Internet of Things. ICC 2020 - 2020 IEEE International Conference on Communications (ICC). doi: https://doi.org/10.1109/icc40277.2020.9149294
  8. Kazlauskas, K., Kazlauskas, J. (2009). Key-Dependent S-Box Generation in AES Block Cipher System. Informatica, 20 (1), 23–34. doi: https://doi.org/10.15388/informatica.2009.235
  9. Preneel, B. (2010). Perspectives on Lightweight Cryptography. Shanghai. Available at: https://homes.esat.kuleuven.be/~preneel/preneel_lightweight_shanghaiv1.pdf
  10. Ivanov, G., Nikolov, N., Nikova, S. (2016). Cryptographically Strong S-Boxes Generated by Modified Immune Algorithm. Lecture Notes in Computer Science, 31–42. doi: https://doi.org/10.1007/978-3-319-29172-7_3
  11. Horbenko, I. D., Horbenko, Yu. I. (2012). Prykladna kryptolohiya. Teoriya. Praktyka. Zastosuvannia. Kharkiv: Vydavnytstvo «Fort», 870.
  12. Dey, S., Ghosh, R. (2018). A Review of Existing 4-Bit Crypto S-Box Cryptanalysis Techniques and Two New Techniques with 4-Bit Boolean Functions for Cryptanalysis of 4-Bit Crypto S-Boxes*. Advances in Pure Mathematics, 08 (03), 272–306. doi: https://doi.org/10.4236/apm.2018.83015
  13. Khompysh, A., Kapalova, N., Algazy, K., Dyusenbayev, D., Sakan, K. (2022). Design of substitution nodes (S-Boxes) of a block cipher intended for preliminary encryption of confidential information. Cogent Engineering, 9 (1). doi: https://doi.org/10.1080/23311916.2022.2080623
  14. Kapalova, N. A., Khaumen, A., Saқan, K. (2020). Rasseivayuschie svoystva lineynykh preobrazovaniy. Mater. nauch. konf. IIVT MON RK «Sovremennye problemy informatiki i vychislitel'nykh tekhnologiy». Almaty, 191–196. Available at: https://conf.iict.kz/wp-content/uploads/2020/10/mpcsct-collection-08.07.2020-final.pdf
  15. Lisitskaya, I. V., Nastenko, A. A. (2011). Great ciphers - casual substitution. Radiotekhnika, 166, 50–55. Available at: https://openarchive.nure.ua/bitstream/document/15255/1/Radiotehnika_V166_2011_rus.pdf
  16. Teh, J. S., Tham, L. J., Jamil, N., Yap, W.-S. (2022). New differential cryptanalysis results for the lightweight block cipher BORON. Journal of Information Security and Applications, 66, 103129. doi: https://doi.org/10.1016/j.jisa.2022.103129
  17. Biham, E., Shamir, A. (1991). Differential Cryptanalysis of DES-like Cryptosystems. Lecture Notes in Computer Science, 2–21. doi: https://doi.org/10.1007/3-540-38424-3_1
  18. Carlet, C. (2010). Vectorial Boolean Functions for Cryptography. Boolean Models and Methods in Mathematics, Computer Science, and Engineering, 398–470. doi: https://doi.org/10.1017/cbo9780511780448.012
  19. Kim, J., Hong, S., Lim, J. (2010). Impossible differential cryptanalysis using matrix method. Discrete Mathematics, 310 (5), 988–1002. doi: https://doi.org/10.1016/j.disc.2009.10.019
  20. Liu, Y., Liang, H., Wang, W., Wang, M. (2017). New Linear Cryptanalysis of Chinese Commercial Block Cipher Standard SM4. Security and Communication Networks, 2017, 1–10. doi: https://doi.org/10.1155/2017/1461520
  21. Matsui, M. (1994). Linear Cryptanalysis Method for DES Cipher. Lecture Notes in Computer Science, 386–397. doi: https://doi.org/10.1007/3-540-48285-7_33
  22. Liu, Z. (2021). Differential-linear cryptanalysis of PRINCE cipher. Chinese Journal of Network and Information Security, 7 (4), 131–140. doi: https://doi.org/10.11959/j.issn.2096-109x.2021072
  23. Biryukov, A., De Cannière, C. (2011). Linear Cryptanalysis for Block Ciphers. Encyclopedia of Cryptography and Security, 722–725. doi: https://doi.org/10.1007/978-1-4419-5906-5_589
  24. Borghoff, J. (2011). 4.6 Linear Cryptanalysis. Cryptanalysis of Lightweight Ciphers. Technical University of Denmark, 60–65. Available at: https://backend.orbit.dtu.dk/ws/portalfiles/portal/5456432/phd-thesis_Julia_Borghoff.pdf
  25. Vergili, I., Yücel, M. D. (2001). Avalanche and Bit Independence Properties for the Ensembles of Randomly Cho-sen S-Boxes. Turkish Journal of Electrical Engineering and Computer Sciences, 9 (2), 137–146. Available at: https://journals.tubitak.gov.tr/elektrik/vol9/iss2/3
  26. Shnayer, B. (2002). Prikladnaya kriptografiya. Moscow:Triumf, 816.
  27. Babenko, L. K., Ischukova, E. A. (2006). Sovremennye algoritmy blochnogo shifrovaniya i metody ikh analiza. Moscow: «Gelios ARV», 376.
  28. Algazy, K. T., Babenko, L. K., Biyashev, R. G., Ishchukova, E. A., Kapalova, N. A., Nysynbaeva, S. E., Smolarz, A. (2020). Differential Cryptanalysis of New Qamal Encryption Algorithm. International journal of electronics and telecommunications, 66 (4), 647–653. doi: https://doi.org/10.24425/ijet.2020.134023
  29. O’Connor, L. (1995). Properties of linear approximation tables. Lecture Notes in Computer Science, 131–136. doi: https://doi.org/10.1007/3-540-60590-8_10
  30. Kuznetsov, A. A., Lisitskaya, I. V., Isaev, S. A. (2011). Lineynye svoystva blochnykh simmetrichnykh shifrov, predstavlennykh na ukrainskiy konkurs. Prikladnaya radioelektronika, 10 (2), 135–140.
  31. Heys, H. M. (2002). A tutorial on linear and differential cryptanalysis. Cryptologia, 26 (3), 189–221. doi: https://doi.org/10.1080/0161-110291890885
  32. Kapalova, N., Sakan, K., Algazy, K., Dyusenbayev, D. (2022). Development and Study of an Encryption Algorithm. Computation, 10 (11), 198. doi: https://doi.org/10.3390/computation10110198
  33. Bogdanov, A., Knudsen, L. R., Leander, G., Paar, C., Poschmann, A., Robshaw, M. J. B. et al. (2007). PRESENT: An Ultra-Lightweight Block Cipher. Lecture Notes in Computer Science, 450–466. doi: https://doi.org/10.1007/978-3-540-74735-2_31
Development of a new lightweight encryption algorithm

Downloads

Published

2023-06-30

How to Cite

Kapalova, N., Algazy, K., & Haumen, A. (2023). Development of a new lightweight encryption algorithm. Eastern-European Journal of Enterprise Technologies, 3(9 (123), 6–19. https://doi.org/10.15587/1729-4061.2023.280055

Issue

Vol. 3 No. 9 (123) (2023): Information and controlling system

Section

Information and controlling system

License

Copyright (c) 2023 Nursulu Kapalova, Kunbolat Algazy, Armanbek Haumen

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.