Construction of a mathematical model and approximate analytical solution to the problem of energy exchange in the «sun ‒ paraboloid concentrator ‒ heat receiver» system

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.282206

Keywords:

paraboloid concentrator, mathematical model, analytical solution, error function, verification of results

Abstract

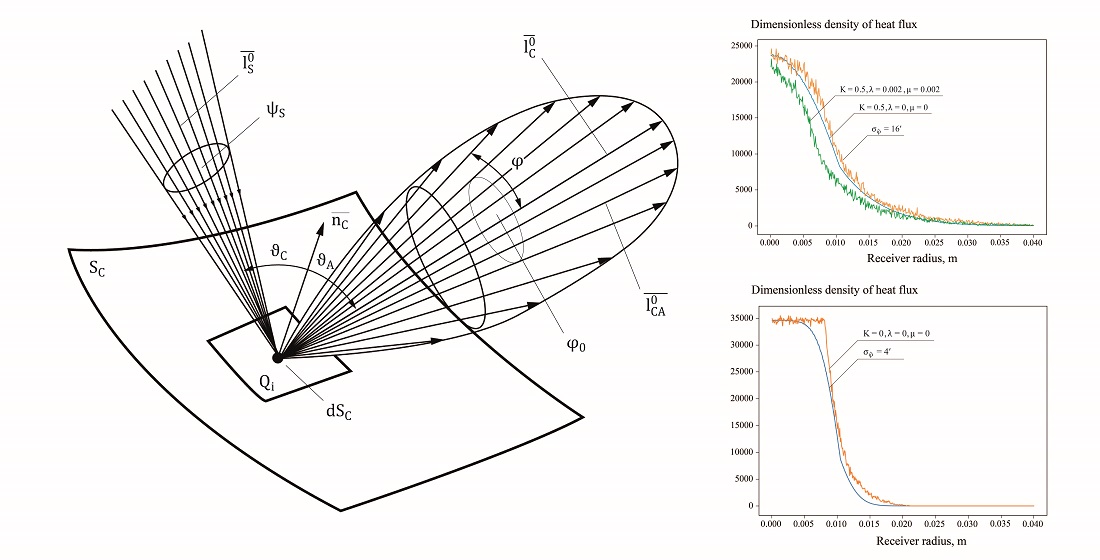
The object of research is the processes of radiation transfer in the «Sun – paraboloid concentrator – heat receiver» system. There are many factors that affect the value of the density of the concentrated heat flux that reaches the surface of the heat sink. The study of the influence of these factors on the overall energy indicators of the system is an important scientific problem that was solved in this work. To solve this problem, a generalized mathematical model of the radiation transfer process in the «Sun – concentrator – heat receiver» system was built, which was adapted for a paraboloid concentrator. The constructed mathematical model was solved by an approximate analytical method, which took into account the integral and discrete parameters of the system, as well as the probability distribution of aberrations of the concentrator surface, its defocusing, and other random influences. The dimensionless density of the heat flux on the surface of the heat sink for a mathematically ideal and real paraboloid concentrator of a fixed geometry was determined. Using the found analytical solution, the results obtained on the basis of the Monte Carlo method were verified. Analytical and numerical results for a mathematically ideal and a real concentrator with minor aberrations and a clear orientation to the Sun agree within the permissible error. For a real concentrator with defocusing, a deviation of numerical data from analytical data was observed. The presence of deviations is associated with a simplification in the interpretation of the analytical probability distribution, in which it is impossible to take into account each influence separately. The obtained analytical results will be useful in the development of real power plants and can be used practically at the stage of checking the adequacy of the system model

Author Biographies

Stanislav Masalykin, Oles Honchar Dnipro National University

Postgraduate Student

Department of Computer Technologies

Lydmila Knysh, Oles Honchar Dnipro National University

Doctor of Technical Sciences, Professor

Department of Computer Technologies

References

  1. Masalykin, S. S., Knysh, L. I. (2021). Monte Carlo algorithm for calculation of radiation transfer in the «sun – parabolic concentrator – heat receiver» system. Problems of Computational Mechanics and Strength of Structures, 33, 114–125. doi: https://doi.org/10.15421/4221010
  2. Masalykin, S., Knysh, L. (2022). Modeling of the energy losses through tracking error for the solar parabolic dish concentrator. Vidnovluvana Energetika, 2 (69), 26–31. doi: https://doi.org/10.36296/1819-8058.2022.2(69).26-31
  3. Allouhi, H., Allouhi, A., Buker, M. S., Zafar, S., Jamil, A. (2022). Recent advances, challenges, and prospects in solar dish collectors: Designs, applications, and optimization frameworks. Solar Energy Materials and Solar Cells, 241, 111743. doi: https://doi.org/10.1016/j.solmat.2022.111743
  4. Kumar, K. H., Daabo, A. M., Karmakar, M. K., Hirani, H. (2022). Solar parabolic dish collector for concentrated solar thermal systems: a review and recommendations. Environmental Science and Pollution Research, 29 (22), 32335–32367. doi: https://doi.org/10.1007/s11356-022-18586-4
  5. Yang, S., Wang, J., Lund, P. D., Jiang, C., Liu, D. (2018). Assessing the impact of optical errors in a novel 2-stage dish concentrator using Monte-Carlo ray-tracing simulation. Renewable Energy, 123, 603–615. doi: https://doi.org/10.1016/j.renene.2018.02.034
  6. Jian, Y., Peng, Y. D., Liu, Y. X. (2022). An optical-mechanical integrated modeling method of solar dish concentrator system for optical performance analysis under service load. Energy, 261, 125283. doi: https://doi.org/10.1016/j.energy.2022.125283
  7. Malik, M. Z., Shaikh, P. H., Zhang, S., Lashari, A. A., Leghari, Z. H., Baloch, M. H. et al. (2022). A review on design parameters and specifications of parabolic solar dish Stirling systems and their applications. Energy Reports, 8, 4128–4154. doi: https://doi.org/10.1016/j.egyr.2022.03.031
  8. Abbas, S., Yuan, Y., Hassan, A., Zhou, J., Ahmed, A., Yang, L., Bisengimana, E. (2023). Effect of the concentration ratio on the thermal performance of a conical cavity tube receiver for a solar parabolic dish concentrator system. Applied Thermal Engineering, 227, 120403. doi: https://doi.org/10.1016/j.applthermaleng.2023.120403
  9. Shuai, Y., Xia, X., Tan, H. (2010). Numerical simulation and experiment research of radiation performance in a dish solar collector system. Frontiers of Energy and Power Engineering in China, 4 (4), 488–495. doi: https://doi.org/10.1007/s11708-010-0007-z
  10. Yan, J., Cheng, Z., Peng, Y. (2018). Effect of Tracking Error of Double-Axis Tracking Device on the Optical Performance of Solar Dish Concentrator. International Journal of Photoenergy, 2018, 1–13. doi: https://doi.org/10.1155/2018/9046127
  11. Jeter, S. M. (1986). The Distribution of Concentrated Solar Radiation in Paraboloidal Collectors. Journal of Solar Energy Engineering, 108 (3), 219–225. doi: https://doi.org/10.1115/1.3268096
  12. Shuai, Y., Xia, X.-L., Tan, H.-P. (2008). Radiation performance of dish solar concentrator/cavity receiver systems. Solar Energy, 82 (1), 13–21. doi: https://doi.org/10.1016/j.solener.2007.06.005
  13. Johnston, G. (1998). Focal region measurements of the 20m2 tiled dish at the Australian National University. Solar Energy, 63 (2), 117–124. doi: https://doi.org/10.1016/s0038-092x(98)00041-3
  14. Peatross, J., Ware, M. (2021). Physics of Light and Optics. Provo, 340.
  15. Stoudenets, V., Slavinska, K. (2019). Numerical calculation of parabolic and parabolic through concentrator parameters for the solar power system based on Stirling engine. Vidnovluvana Energetika, 1 (56), 36–44. doi: https://doi.org/10.36296/1819-8058.2022.2(69).26-31 https://doi.org/10.36296/1819-8058.2019.1(56).36-44
  16. Vittal, P. R. (2013). Analytical Geometry: 2D and 3D. Pearson India, 748.
  17. Grilikhes, V. A., Matveev, V. M., Poluektov, V. P. (1975). Solnechnye vysokotemperaturnye istochniki tepla dlya kosmicheskikh apparatov. Moscow: Mashinostroenie, 248.
  18. Klenke, A. (2014). Probability Theory: A Comprehensive Course. Springer, 638. doi: https://doi.org/10.1007/978-1-4471-5361-0
  19. Cinlar, E. (2011). Probability and Stochastics. Springer Science & Business Media, 558.
  20. Knysh, L. (2021). Comprehensive mathematical model and efficient numerical analysis of the design parameters of the parabolic trough receiver. International Journal of Thermal Sciences, 162, 106777. doi: https://doi.org/10.1016/j.ijthermalsci.2020.106777
  21. Knysh, L. (2022). Thermo-fluid modeling and thermodynamic analysis of low-temperature parabolic trough systems with multi-walled carbon nanotubes/water nanofluids. International Journal of Thermal Sciences, 181, 107770. doi: https://doi.org/10.1016/j.ijthermalsci.2022.107770
Construction of a mathematical model and approximate analytical solution to the problem of energy exchange in the «sun ‒ paraboloid concentrator ‒ heat receiver» system

Downloads

Published

2023-06-30

How to Cite

Masalykin, S., & Knysh, L. (2023). Construction of a mathematical model and approximate analytical solution to the problem of energy exchange in the «sun ‒ paraboloid concentrator ‒ heat receiver» system. Eastern-European Journal of Enterprise Technologies, 3(8 (123), 37–45. https://doi.org/10.15587/1729-4061.2023.282206

Issue

Vol. 3 No. 8 (123) (2023): Energy-saving technologies and equipment

Section

Energy-saving technologies and equipment

License

Copyright (c) 2023 Stanislav Masalykin, Lydmila Knysh

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.