Construction of mathematical model of particle movement by an inclined screw rotating in a fixed casing
DOI:
https://doi.org/10.15587/1729-4061.2023.288548Keywords:
force applied to a particle, differential equations of motion, cylindrical casing, angle of inclination of the screwAbstract
Screw conveyors are used to move bulk materials vertically upwards, horizontally, and at an angle to the horizon. The processes that take place when particles are moved by a screw conveyor in vertical and horizontal directions have been studied. There is a significant difference between them: for transportation in the vertical direction, the necessary conditions must be ensured (sufficient angular speed of rotation of the screw), and for horizontal transportation, the movement of the particle occurs at any angular speed of rotation of the screw. Therefore, when changing the inclination of the axis of the screw, there comes a moment when transportation becomes possible, while it was impossible in the vertical direction.
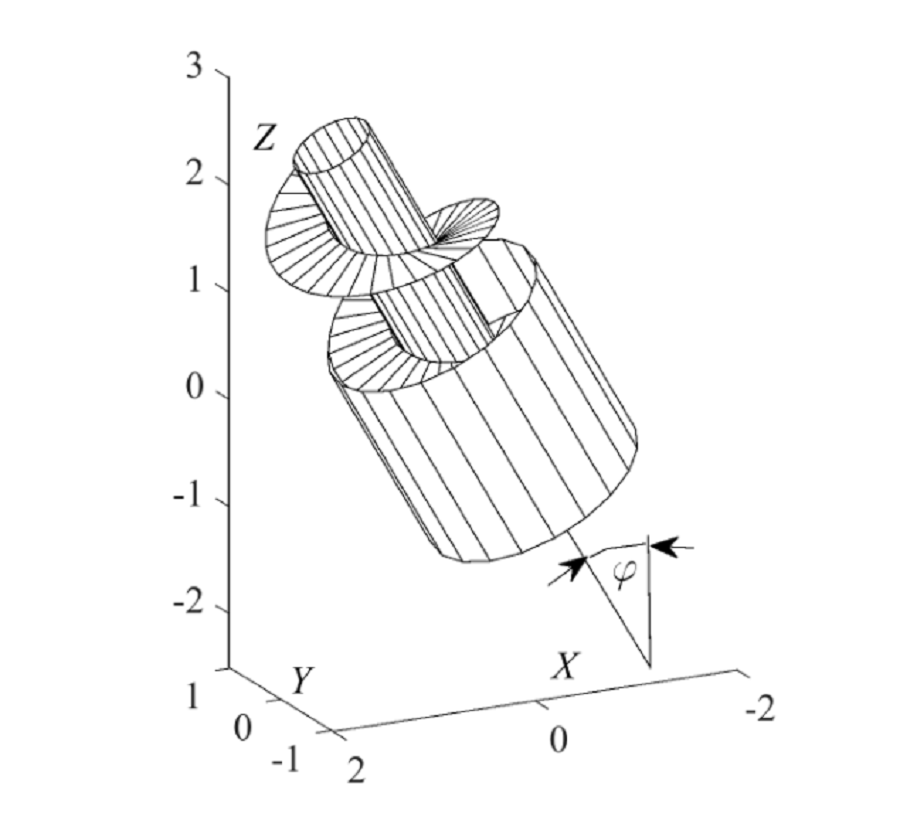
This paper considers the movement of a particle under the condition that it simultaneously contacts two surfaces: the moving surface of the screw and the stationary surface of the cylindrical casing in which the screw rotates. Their common line along which the particle slides is a helical line – the periphery of the screw. The particle slides along the helical line of the rotating screw, i.e., it is in relative motion with respect to it. At the same time, it slides along the surface of the casing, relative to which it is in absolute motion. The trajectory of the particle's absolute motion is its sliding track on the casing surface.
When constructing differential equations of the relative motion of particles, the forces applied to the particle were taken into account. The initial position was taken to be the vertical direction of the screw to transport the particle upwards. If an auger in a cylindrical casing is tilted from the vertical direction to a certain angle, then all applied forces (except the force of weight) will also tilt to this angle. On the basis of this, generalized differential equations of the relative motion of a particle during its transportation by an inclined screw were built. They made it possible to derive a generalized mathematical model of the movement of a particle by an inclined screw that rotates inside a fixed casing
References
- Gaponova, O. P., Antoszewski, B., Tarelnyk, V. B., Kurp, P., Myslyvchenko, O. M., Tarelnyk, N. V. (2021). Analysis of the Quality of Sulfomolybdenum Coatings Obtained by Electrospark Alloying Methods. Materials, 14 (21), 6332. doi: https://doi.org/10.3390/ma14216332
- Tarelnyk, V. B., Konoplianchenko, Ie. V., Gaponova, O. P., Tarelnyk, N. V., Martsynkovskyy, V. S., Sarzhanov, B. O. et al. (2020). Effect of Laser Processing on the Qualitative Parameters of Protective Abrasion-Resistant Coatings. Powder Metallurgy and Metal Ceramics, 58 (11-12), 703–713. doi: https://doi.org/10.1007/s11106-020-00127-8
- Gorobets, V., Trokhaniak, V., Bohdan, Y., Antypov, I. (2021). Numerical Modeling Of Heat Transfer And Hydrodynamics In Compact Shifted Arrangement Small Diameter Tube Bundles. Journal of Applied and Computational Mechanics, 7 (1), 292–301. doi: https://doi.org/10.22055/jacm.2020.31007.1855
- Pankiv, M., Pylypets, M., Pankiv, V., Pankiv, Y., Dubchak, N. (2022). Methodology for refining the performance of screw conveyor. Scientific Journal of the Ternopil National Technical University, 105 (1), 95–107. doi: https://doi.org/10.33108/visnyk_tntu2022.01.095
- Rogatynskyi, R., Hevko, I., Diachun, A., Rogatynska, O., Melnychuk, A. (2019). The cargo movement model by the screw conveyor surfaces with the rotating casing. Scientific Journal of the Ternopil National Technical University, 92 (4), 34–41. doi: https://doi.org/10.33108/visnyk_tntu2018.04.034
- Djuraev, A., Yuldashev, K., Teshaboyev, O. (2023). Theoretical studies on screw conveyor for transportation and cleaning of linter and design of constructive parameters of transmissions. Scientific and Technical Journal of Namangan Institute of Engineering and Technology, 8 (1), 29–35. doi: https://doi.org/10.5281/zenodo.7945187
- To'raev, S. A., Rahmatov, S. M. (2022). Development of an effective design and justification of the parameters of the screw conveyor for the transportation and cleaning of cotton. Universum, 2 (95). Available at: https://7universum.com/ru/tech/archive/item/13150
- Rohatynskyi, R., Gevko, I., Diachun, A., Lyashuk, O., Skyba, O., Melnychuk, A. (2019). Feasibility Study of Improving the Transport Performance by Means of Screw Conveyors with Rotary Casings. Acta Technologica Agriculturae, 22 (4), 140–145. doi: https://doi.org/10.2478/ata-2019-0025
- Volina, T., Pylypaka, S., Nesvidomin, V., Pavlov, A., Dranovska, S. (2021). The possibility to apply the Frenet trihedron and formulas for the complex movement of a point on a plane with the predefined plane displacement. Eastern-European Journal of Enterprise Technologies, 3 (7 (111)), 45–50. doi: https://doi.org/10.15587/1729-4061.2021.232446
- Ahmed, A. K., Nesvidomin, A., Pylypaka, S., Volina, T., Dieniezhnikov, S. (2023). Determining regularities in the construction of curves and surfaces using the Darboux trihedron. Eastern-European Journal of Enterprise Technologies, 3 (1 (123)), 6–12. doi: https://doi.org/10.15587/1729-4061.2023.279007
- Pylypaka, S. F., Nesvidomin, V. M., Klendii, M. B., Rogovskii, I. L., Kresan, T. A., Trokhaniak, V. I. (2019). Conveyance of a particle by a vertical screw, which is limited by a coaxial fixed cylinder. Bulletin Of The Karaganda University-Mathematics, 95 (3), 108–119. doi: https://doi.org/10.31489/2019m2/108-119
- Pylypaka, S., Volina, T., Nesvidomin, A., Babka, V., Shuliak, I. (2022). The transportation of the material particle by the vertical auger. Applied Geometry And Engineering Graphics, 102, 165–180. doi: https://doi.org/10.32347/0131-579x.2022.102.165-180
- Lyubin, M., Tokarchuk, O., Yaropud, V. (2016). Features of work of steeply inclined spiral conveyers are at moving of corn products. Tekhnika, enerhetyka, transport APK, 3 (95), 235–240. Available at: https://journals.indexcopernicus.com/api/file/viewByFileId/1086461.pdf
- Serilko, L. S., Shchuryk, V. O., Serilko, D. L. (2014). Calculation of feeders’ parameters of horizontal helical conveyors. Visnyk Natsionalnoho universytetu vodnoho hospodarstva ta pryrodokorystuvannia. Tekhnichni nauky, 4, 300–307. Available at: http://nbuv.gov.ua/UJRN/Vnuvgp_tekhn_2014_4_37
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Tetiana Volina, Serhii Pylypaka, Mykhailo Kalenyk, Serhii Dieniezhnikov, Viktor Nesvidomin, Iryna Hryshchenko, Yana Lytvynenko, Artem Borodai, Dmytro Borodai, Yana Borodai

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









