Розробка математичної моделі переміщення частинки похилим шнеком, який обертається в нерухомому кожусі
DOI:
https://doi.org/10.15587/1729-4061.2023.288548Ключові слова:
прикладені до частинки сили, диференціальні рівняння руху, циліндричний кожух, кут нахилу шнекаАнотація
Гвинтові транспортери використовуються для переміщення сипких матеріалів вертикально вгору, в горизонтальному напрямі, а також під кутом до горизонту. Вивченими є процеси, які відбуваються при переміщенні частинки шнековим транспортером у вертикальному і горизонтальному напрямах. Між ними є суттєва різниця: для транспортування у вертикальному напрямі потрібно забезпечити необхідні умови (достатню кутову швидкість обертання шнека), а при горизонтальному транспортуванні переміщення частинки відбувається при будь-якій кутовій швидкості обертання шнека. Отже, при зміні нахилу осі шнека наступає момент, коли транспортування стає можливим, тоді як воно було неможливим у вертикальному напрямі.
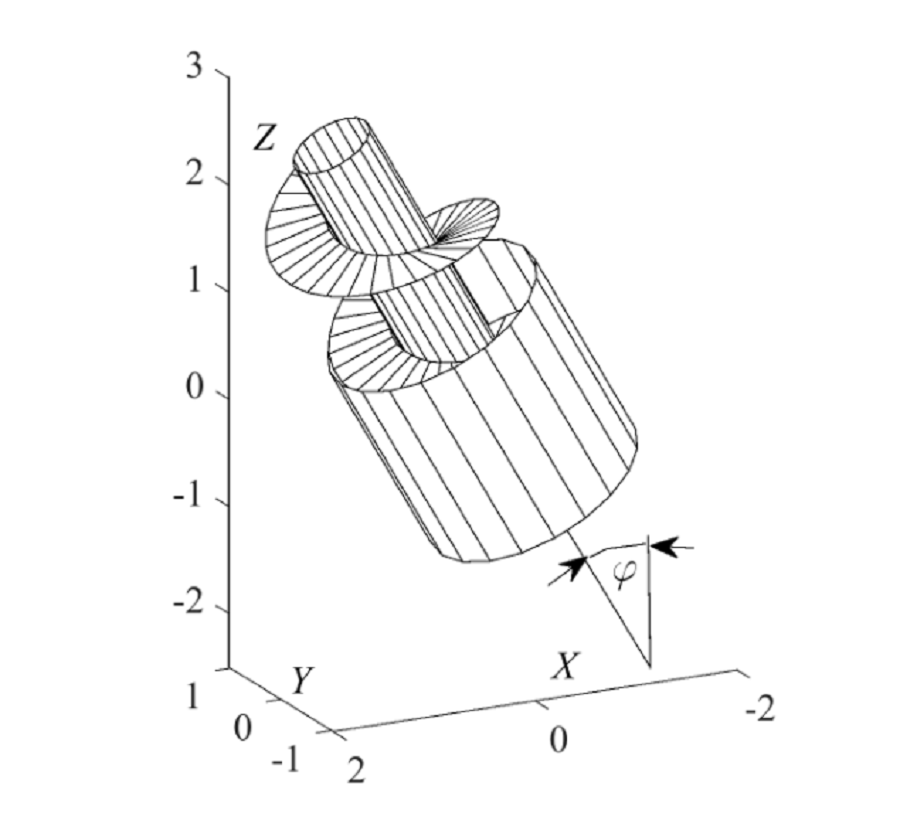
У статті розглянуто рух частинки за умови, що вона одночасно контактує з двома поверхнями: рухомою поверхнею шнека і нерухомою поверхнею циліндричного кожуха, у якому обертається шнек. Їх спільною лінією, по якій ковзає частинка, є гвинтова лінія – периферія шнека. Частинка ковзає по гвинтовій лінії шнека, який обертається, тобто по відношенню до нього вона перебуває у відносному русі. Одночасно вона ковзає і по поверхні кожуха, по відношенню до якого вона перебуває в абсолютному русі. Траєкторією абсолютного руху частинки є її слід ковзання на поверхні кожуха.
При складанні диференціальних рівнянь відносного руху частинки враховувалися прикладені до частинки сили. За початкове положення було прийнято вертикальний напрям шнека для транспортування частинки вгору. Якщо шнек у циліндричному кожусі нахиляти від вертикального напряму на певний кут, то і всі прикладені сили (окрім сили ваги) теж будуть нахилятися на цей кут. На основі цього складено узагальненні диференціальні рівняння відносного руху частинки при її транспортування похилим шнеком. Вони дали можливість отримати узагальнену математичну модель переміщення частинки похилим шнеком, який обертається всередині нерухомого кожуха
Посилання
- Gaponova, O. P., Antoszewski, B., Tarelnyk, V. B., Kurp, P., Myslyvchenko, O. M., Tarelnyk, N. V. (2021). Analysis of the Quality of Sulfomolybdenum Coatings Obtained by Electrospark Alloying Methods. Materials, 14 (21), 6332. doi: https://doi.org/10.3390/ma14216332
- Tarelnyk, V. B., Konoplianchenko, Ie. V., Gaponova, O. P., Tarelnyk, N. V., Martsynkovskyy, V. S., Sarzhanov, B. O. et al. (2020). Effect of Laser Processing on the Qualitative Parameters of Protective Abrasion-Resistant Coatings. Powder Metallurgy and Metal Ceramics, 58 (11-12), 703–713. doi: https://doi.org/10.1007/s11106-020-00127-8
- Gorobets, V., Trokhaniak, V., Bohdan, Y., Antypov, I. (2021). Numerical Modeling Of Heat Transfer And Hydrodynamics In Compact Shifted Arrangement Small Diameter Tube Bundles. Journal of Applied and Computational Mechanics, 7 (1), 292–301. doi: https://doi.org/10.22055/jacm.2020.31007.1855
- Pankiv, M., Pylypets, M., Pankiv, V., Pankiv, Y., Dubchak, N. (2022). Methodology for refining the performance of screw conveyor. Scientific Journal of the Ternopil National Technical University, 105 (1), 95–107. doi: https://doi.org/10.33108/visnyk_tntu2022.01.095
- Rogatynskyi, R., Hevko, I., Diachun, A., Rogatynska, O., Melnychuk, A. (2019). The cargo movement model by the screw conveyor surfaces with the rotating casing. Scientific Journal of the Ternopil National Technical University, 92 (4), 34–41. doi: https://doi.org/10.33108/visnyk_tntu2018.04.034
- Djuraev, A., Yuldashev, K., Teshaboyev, O. (2023). Theoretical studies on screw conveyor for transportation and cleaning of linter and design of constructive parameters of transmissions. Scientific and Technical Journal of Namangan Institute of Engineering and Technology, 8 (1), 29–35. doi: https://doi.org/10.5281/zenodo.7945187
- To'raev, S. A., Rahmatov, S. M. (2022). Development of an effective design and justification of the parameters of the screw conveyor for the transportation and cleaning of cotton. Universum, 2 (95). Available at: https://7universum.com/ru/tech/archive/item/13150
- Rohatynskyi, R., Gevko, I., Diachun, A., Lyashuk, O., Skyba, O., Melnychuk, A. (2019). Feasibility Study of Improving the Transport Performance by Means of Screw Conveyors with Rotary Casings. Acta Technologica Agriculturae, 22 (4), 140–145. doi: https://doi.org/10.2478/ata-2019-0025
- Volina, T., Pylypaka, S., Nesvidomin, V., Pavlov, A., Dranovska, S. (2021). The possibility to apply the Frenet trihedron and formulas for the complex movement of a point on a plane with the predefined plane displacement. Eastern-European Journal of Enterprise Technologies, 3 (7 (111)), 45–50. doi: https://doi.org/10.15587/1729-4061.2021.232446
- Ahmed, A. K., Nesvidomin, A., Pylypaka, S., Volina, T., Dieniezhnikov, S. (2023). Determining regularities in the construction of curves and surfaces using the Darboux trihedron. Eastern-European Journal of Enterprise Technologies, 3 (1 (123)), 6–12. doi: https://doi.org/10.15587/1729-4061.2023.279007
- Pylypaka, S. F., Nesvidomin, V. M., Klendii, M. B., Rogovskii, I. L., Kresan, T. A., Trokhaniak, V. I. (2019). Conveyance of a particle by a vertical screw, which is limited by a coaxial fixed cylinder. Bulletin Of The Karaganda University-Mathematics, 95 (3), 108–119. doi: https://doi.org/10.31489/2019m2/108-119
- Pylypaka, S., Volina, T., Nesvidomin, A., Babka, V., Shuliak, I. (2022). The transportation of the material particle by the vertical auger. Applied Geometry And Engineering Graphics, 102, 165–180. doi: https://doi.org/10.32347/0131-579x.2022.102.165-180
- Lyubin, M., Tokarchuk, O., Yaropud, V. (2016). Features of work of steeply inclined spiral conveyers are at moving of corn products. Tekhnika, enerhetyka, transport APK, 3 (95), 235–240. Available at: https://journals.indexcopernicus.com/api/file/viewByFileId/1086461.pdf
- Serilko, L. S., Shchuryk, V. O., Serilko, D. L. (2014). Calculation of feeders’ parameters of horizontal helical conveyors. Visnyk Natsionalnoho universytetu vodnoho hospodarstva ta pryrodokorystuvannia. Tekhnichni nauky, 4, 300–307. Available at: http://nbuv.gov.ua/UJRN/Vnuvgp_tekhn_2014_4_37
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2023 Tetiana Volina, Serhii Pylypaka, Mykhailo Kalenyk, Serhii Dieniezhnikov, Viktor Nesvidomin, Iryna Hryshchenko, Yana Lytvynenko, Artem Borodai, Dmytro Borodai, Yana Borodai

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









