Mathematical model for optimization in air traffic scheduling management during the COVID-19 pandemic

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.293514

Keywords:

flight scheduling management, mathematical models, algorithms, optimization, COVID-19 pandemic

Abstract

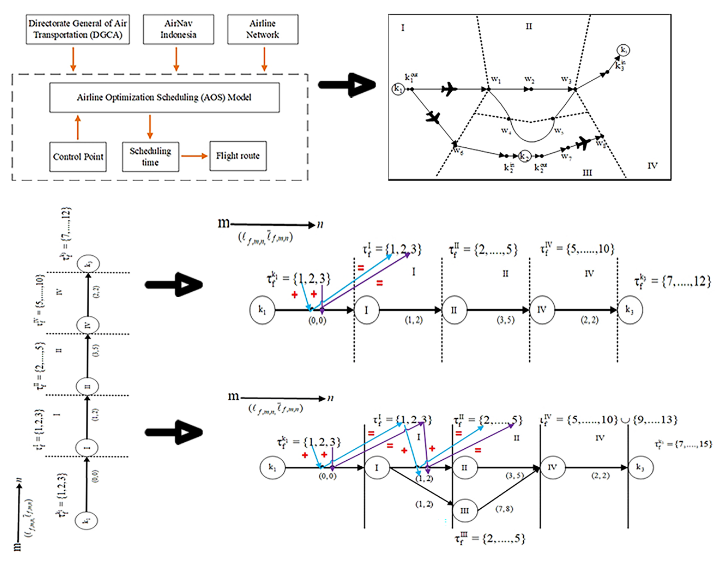
In this paper, the object of the study is determining air traffic scheduling management by optimizing mathematical models. The problem in this study is that the COVID-19 pandemic has significantly disrupted air traffic, resulting in changes to regulations, travel restrictions and a decrease in passenger demand. One of the problems that must be resolved is how to organize and adapt flight schedules to current conditions by focusing on mathematical models that are used to optimize or increase the efficiency of managing flight schedules or air traffic. Mathematical models can help find ways to optimize the use of available resources, such as airport capacity, flight routes and flight frequency. The results obtained in this research are a mathematical model that specifically takes into account the variables involved in setting air traffic schedules during the COVID-19 pandemic so that capacity limits at airports and airspace are always normal. An optimization model was developed from previous research, namely the model that takes into account ground and air delays as well as the use of alternative paths and avoids deviations from the initial more accurate flight plan, which overall indicates that the maximum time and maximum distance values for each item have been optimized to achieve better values. This research has the novelty of producing a mathematical model using variables, objective functions, capacity limits, flight structure limits and variable domains, which then produces an algorithm with data input processes, determining optimization models, determining variables, determining objective functions, determining problems. The results of this model can be recommended to airlines in scheduling flights during the pandemic

Author Biographies

Darmeli Nasution, Universitas Sumatera Utara

Master of Computer

Department of Computer Science

Herman Mawengkang, Universitas Sumatera Utara

Master of Computer

Department of Computer Science

Fahmi, Universitas Sumatera Utara

Master of Computer

Department of Electrical Engineering

Muhammad Zarlis, BINUS University

Master of Computer

Department of Information System Management

References

  1. Lin, Y. (2021). Spoken Instruction Understanding in Air Traffic Control: Challenge, Technique, and Application. Aerospace, 8 (3), 65. doi: https://doi.org/10.3390/aerospace8030065
  2. Ortner, P., Steinhöfler, R., Leitgeb, E., Flühr, H. (2022). Augmented Air Traffic Control System—Artificial Intelligence as Digital Assistance System to Predict Air Traffic Conflicts. AI, 3 (3), 623–644. doi: https://doi.org/10.3390/ai3030036
  3. Štimac, I., Vidović, A., Mihetec, T., Drljača, M. (2020). Optimization of Airport Capacity Efficiency by Selecting Optimal Aircraft and Airline Business Model. Sustainability, 12 (10), 3988. doi: https://doi.org/10.3390/su12103988
  4. Ivanov, N., Netjasov, F., Jovanović, R., Starita, S., Strauss, A. (2017). Air Traffic Flow Management slot allocation to minimize propagated delay and improve airport slot adherence. Transportation Research Part A: Policy and Practice, 95, 183–197. doi: https://doi.org/10.1016/j.tra.2016.11.010
  5. Nurjanni, K. P., Carvalho, M. S., Costa, L. (2017). Green supply chain design: A mathematical modeling approach based on a multi-objective optimization model. International Journal of Production Economics, 183, 421–432. doi: https://doi.org/10.1016/j.ijpe.2016.08.028
  6. Du, G., Zhang, Y., Liu, X., Jiao, R. J., Xia, Y., Li, Y. (2019). A review of leader-follower joint optimization problems and mathematical models for product design and development. The International Journal of Advanced Manufacturing Technology, 103 (9-12), 3405–3424. doi: https://doi.org/10.1007/s00170-019-03612-6
  7. Kaidi, W., Khishe, M., Mohammadi, M. (2022). Dynamic Levy Flight Chimp Optimization. Knowledge-Based Systems, 235, 107625. doi: https://doi.org/10.1016/j.knosys.2021.107625
  8. Degas, A., Islam, M. R., Hurter, C., Barua, S., Rahman, H., Poudel, M. et al. (2022). A Survey on Artificial Intelligence (AI) and eXplainable AI in Air Traffic Management: Current Trends and Development with Future Research Trajectory. Applied Sciences, 12 (3), 1295. doi: https://doi.org/10.3390/app12031295
  9. Mélan, C., Cascino, N. (2022). Effects of a modified shift work organization and traffic load on air traffic controllers’ sleep and alertness during work and non-work activities. Applied Ergonomics, 98, 103596. doi: https://doi.org/10.1016/j.apergo.2021.103596
  10. Deveci, M., Çiftçi, M. E., Akyurt, İ. Z., Gonzalez, E. D. R. S. (2022). Impact of COVID-19 pandemic on the Turkish civil aviation industry. Sustainable Operations and Computers, 3, 93–102. doi: https://doi.org/10.1016/j.susoc.2021.11.002
  11. Szabo, S., Makó, S., Kešeľová, M., Szabo, S. (2021). Design of a Unified Algorithm to Ensure the Sustainable Use of Air Transport during a Pandemic. Sustainability, 13 (11), 5970. doi: https://doi.org/10.3390/su13115970
  12. García-Heredia, D., Alonso-Ayuso, A., Molina, E. (2019). A Combinatorial model to optimize air traffic flow management problems. Computers & Operations Research, 112, 104768. doi: https://doi.org/10.1016/j.cor.2019.104768
  13. Sandamali, G. G. N., Su, R., Sudheera, K. L. K., Zhang, Y. (2022). A Safety-Aware Real-Time Air Traffic Flow Management Model Under Demand and Capacity Uncertainties. IEEE Transactions on Intelligent Transportation Systems, 23 (7), 8615–8628. doi: https://doi.org/10.1109/tits.2021.3083964
  14. Ntakolia, C., Lyridis, D. V. (2022). A n − D ant colony optimization with fuzzy logic for air traffic flow management. Operational Research, 22 (5), 5035–5053. doi: https://doi.org/10.1007/s12351-021-00686-7
  15. Shone, R., Glazebrook, K., Zografos, K. G. (2021). Applications of stochastic modeling in air traffic management: Methods, challenges and opportunities for solving air traffic problems under uncertainty. European Journal of Operational Research, 292 (1), 1–26. doi: https://doi.org/10.1016/j.ejor.2020.10.039
  16. Samà, M., D’Ariano, A., D’Ariano, P., Pacciarelli, D. (2017). Scheduling models for optimal aircraft traffic control at busy airports: Tardiness, priorities, equity and violations considerations. Omega, 67, 81–98. doi: https://doi.org/10.1016/j.omega.2016.04.003
  17. Jamili, A. (2017). A robust mathematical model and heuristic algorithms for integrated aircraft routing and scheduling, with consideration of fleet assignment problem. Journal of Air Transport Management, 58, 21–30. doi: https://doi.org/10.1016/j.jairtraman.2016.08.008
  18. Zhang, L., Li, Z., Królczyk, G., Wu, D., Tang, Q. (2019). Mathematical modeling and multi-attribute rule mining for energy efficient job-shop scheduling. Journal of Cleaner Production, 241, 118289. doi: https://doi.org/10.1016/j.jclepro.2019.118289
  19. Correa Issi, G., Linfati, R., Escobar, J. W. (2020). Mathematical Optimization Model for Truck Scheduling in a Distribution Center with a Mixed Service-Mode Dock Area. Journal of Advanced Transportation, 2020, 1–13. doi: https://doi.org/10.1155/2020/8813372
  20. Hammad, A. W., Grzybowska, H., Sutrisna, M., Akbarnezhad, A., Haddad, A. (2019). A novel mathematical optimisation model for the scheduling of activities in modular construction factories. Construction Management and Economics, 38 (6), 534–551. doi: https://doi.org/10.1080/01446193.2019.1682174
  21. Vital-Soto, A., Azab, A., Baki, M. F. (2020). Mathematical modeling and a hybridized bacterial foraging optimization algorithm for the flexible job-shop scheduling problem with sequencing flexibility. Journal of Manufacturing Systems, 54, 74–93. doi: https://doi.org/10.1016/j.jmsy.2019.11.010
  22. Evler, J., Asadi, E., Preis, H., Fricke, H. (2021). Airline ground operations: Schedule recovery optimization approach with constrained resources. Transportation Research Part C: Emerging Technologies, 128, 103129. doi: https://doi.org/10.1016/j.trc.2021.103129
  23. Xia, Q., Xu, S. (2023). Ramified Optimal Transportation with Payoff on the Boundary. SIAM Journal on Mathematical Analysis, 55 (1), 186–209. doi: https://doi.org/10.1137/20m1367714
  24. Ciarlet, P., Kachanovska, M. (2022). A Mathematical Study of a Hyperbolic Metamaterial in Free Space. SIAM Journal on Mathematical Analysis, 54 (2), 2216–2250. doi: https://doi.org/10.1137/21m1404223
  25. Ahmad, H., A. Khan, T., Yao, S.-W. (2020). Numerical solution of second order Painlevé differential equation. Journal of Mathematics and Computer Science, 150–157. doi: https://doi.org/10.22436/jmcs.021.02.06
  26. Agustín, A., Alonso-Ayuso, A., Escudero, L. F., Pizarro, C. (2010). Mathematical optimization models for air traffic flow management: A review. Available at: https://burjcdigital.urjc.es/handle/10115/3405
  27. Bertsimas, D., Patterson, S. S. (2000). The Traffic Flow Management Rerouting Problem in Air Traffic Control: A Dynamic Network Flow Approach. Transportation Science, 34 (3), 239–255. doi: https://doi.org/10.1287/trsc.34.3.239.12300
Mathematical model for optimization in air traffic scheduling management during the COVID-19 pandemic

Downloads

Published

2023-12-28

How to Cite

Nasution, D., Mawengkang, H., Fahmi, & Zarlis, M. (2023). Mathematical model for optimization in air traffic scheduling management during the COVID-19 pandemic. Eastern-European Journal of Enterprise Technologies, 6(3 (126), 18–26. https://doi.org/10.15587/1729-4061.2023.293514

Issue

Vol. 6 No. 3 (126) (2023): Control processes

Section

Control processes

License

Copyright (c) 2023 Darmeli Nasution, Herman Mawengkang, Fahmi, Muhammad Zarlis

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.