Математична модель для оптимізації управління розкладом повітряного руху під час пандемії COVID-19

Автор(и)

DOI:

https://doi.org/10.15587/1729-4061.2023.293514

Ключові слова:

управління розкладом польотів, математичні моделі, алгоритми, оптимізація, пандемія COVID-19

Анотація

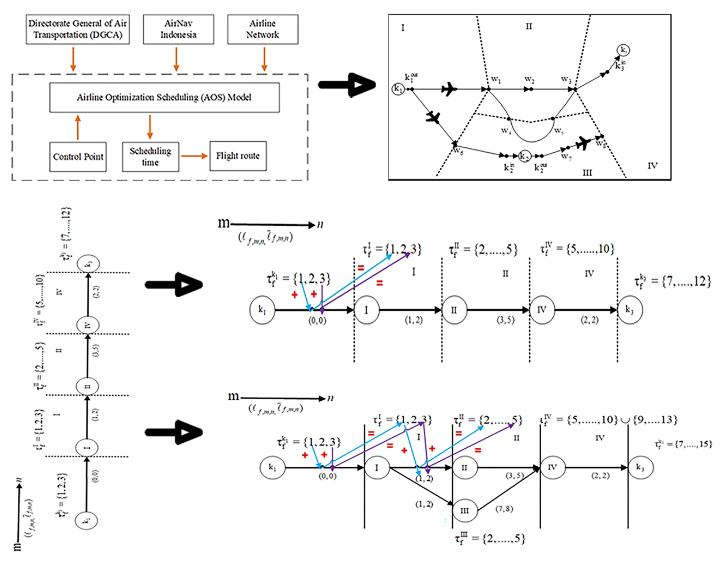
У роботі об’єктом дослідження є управління розкладом повітряного руху шляхом оптимізації математичних моделей. Проблема в дослідженні полягає в тому, що пандемія COVID-19 спричинила значні перебої у повітряному сполученні, що призвело до змін у правилах, обмежень на поїздки та зниження попиту пасажирів. Одне із завдань, яке необхідно вирішити, є те, як організувати та адаптувати розклад польотів до поточних умов, орієнтуючись на математичні моделі, які використовуються для оптимізації або підвищення ефективності управління розкладом польотів або повітряним рухом. Математичні моделі дозволяють знайти способи оптимізації використання наявних ресурсів, таких як пропускна спроможність аеропорту, маршрути польотів та частота рейсів. Результати, отримані в дослідженні, являють собою математичну модель, яка конкретно враховує змінні, що беруть участь у встановленні графіків повітряного руху під час пандемії COVID-19 з тим, щоб обмеження пропускної спроможності в аеропортах і повітряному просторі завжди залишалися в межах норми. На основі попередніх досліджень була розроблена оптимізаційна модель, а саме модель, що враховує наземні та повітряні затримки, а також використання альтернативних маршрутів і дозволяє уникнути відхилень від початкового більш точного плану польоту, що в цілому вказує на те, що максимальний час і максимальна відстань для кожного елемента були оптимізовані для досягнення кращих значень. Новизна даного дослідження полягає у створенні математичної моделі з використанням змінних, цільових функцій, меж пропускної спроможності, меж структури польоту та змінних областей, що дозволяє створити алгоритм з процесами введення даних, визначенням оптимізаційних моделей, змінних, цільових функцій та завдань. Результати цієї моделі можуть бути рекомендовані авіакомпаніям при плануванні рейсів під час пандемії

Біографії авторів

Darmeli Nasution, Universitas Sumatera Utara

Master of Computer

Department of Computer Science

Herman Mawengkang, Universitas Sumatera Utara

Master of Computer

Department of Computer Science

Fahmi, Universitas Sumatera Utara

Master of Computer

Department of Electrical Engineering

Muhammad Zarlis, BINUS University

Master of Computer

Department of Information System Management

Посилання

  1. Lin, Y. (2021). Spoken Instruction Understanding in Air Traffic Control: Challenge, Technique, and Application. Aerospace, 8 (3), 65. doi: https://doi.org/10.3390/aerospace8030065
  2. Ortner, P., Steinhöfler, R., Leitgeb, E., Flühr, H. (2022). Augmented Air Traffic Control System—Artificial Intelligence as Digital Assistance System to Predict Air Traffic Conflicts. AI, 3 (3), 623–644. doi: https://doi.org/10.3390/ai3030036
  3. Štimac, I., Vidović, A., Mihetec, T., Drljača, M. (2020). Optimization of Airport Capacity Efficiency by Selecting Optimal Aircraft and Airline Business Model. Sustainability, 12 (10), 3988. doi: https://doi.org/10.3390/su12103988
  4. Ivanov, N., Netjasov, F., Jovanović, R., Starita, S., Strauss, A. (2017). Air Traffic Flow Management slot allocation to minimize propagated delay and improve airport slot adherence. Transportation Research Part A: Policy and Practice, 95, 183–197. doi: https://doi.org/10.1016/j.tra.2016.11.010
  5. Nurjanni, K. P., Carvalho, M. S., Costa, L. (2017). Green supply chain design: A mathematical modeling approach based on a multi-objective optimization model. International Journal of Production Economics, 183, 421–432. doi: https://doi.org/10.1016/j.ijpe.2016.08.028
  6. Du, G., Zhang, Y., Liu, X., Jiao, R. J., Xia, Y., Li, Y. (2019). A review of leader-follower joint optimization problems and mathematical models for product design and development. The International Journal of Advanced Manufacturing Technology, 103 (9-12), 3405–3424. doi: https://doi.org/10.1007/s00170-019-03612-6
  7. Kaidi, W., Khishe, M., Mohammadi, M. (2022). Dynamic Levy Flight Chimp Optimization. Knowledge-Based Systems, 235, 107625. doi: https://doi.org/10.1016/j.knosys.2021.107625
  8. Degas, A., Islam, M. R., Hurter, C., Barua, S., Rahman, H., Poudel, M. et al. (2022). A Survey on Artificial Intelligence (AI) and eXplainable AI in Air Traffic Management: Current Trends and Development with Future Research Trajectory. Applied Sciences, 12 (3), 1295. doi: https://doi.org/10.3390/app12031295
  9. Mélan, C., Cascino, N. (2022). Effects of a modified shift work organization and traffic load on air traffic controllers’ sleep and alertness during work and non-work activities. Applied Ergonomics, 98, 103596. doi: https://doi.org/10.1016/j.apergo.2021.103596
  10. Deveci, M., Çiftçi, M. E., Akyurt, İ. Z., Gonzalez, E. D. R. S. (2022). Impact of COVID-19 pandemic on the Turkish civil aviation industry. Sustainable Operations and Computers, 3, 93–102. doi: https://doi.org/10.1016/j.susoc.2021.11.002
  11. Szabo, S., Makó, S., Kešeľová, M., Szabo, S. (2021). Design of a Unified Algorithm to Ensure the Sustainable Use of Air Transport during a Pandemic. Sustainability, 13 (11), 5970. doi: https://doi.org/10.3390/su13115970
  12. García-Heredia, D., Alonso-Ayuso, A., Molina, E. (2019). A Combinatorial model to optimize air traffic flow management problems. Computers & Operations Research, 112, 104768. doi: https://doi.org/10.1016/j.cor.2019.104768
  13. Sandamali, G. G. N., Su, R., Sudheera, K. L. K., Zhang, Y. (2022). A Safety-Aware Real-Time Air Traffic Flow Management Model Under Demand and Capacity Uncertainties. IEEE Transactions on Intelligent Transportation Systems, 23 (7), 8615–8628. doi: https://doi.org/10.1109/tits.2021.3083964
  14. Ntakolia, C., Lyridis, D. V. (2022). A n − D ant colony optimization with fuzzy logic for air traffic flow management. Operational Research, 22 (5), 5035–5053. doi: https://doi.org/10.1007/s12351-021-00686-7
  15. Shone, R., Glazebrook, K., Zografos, K. G. (2021). Applications of stochastic modeling in air traffic management: Methods, challenges and opportunities for solving air traffic problems under uncertainty. European Journal of Operational Research, 292 (1), 1–26. doi: https://doi.org/10.1016/j.ejor.2020.10.039
  16. Samà, M., D’Ariano, A., D’Ariano, P., Pacciarelli, D. (2017). Scheduling models for optimal aircraft traffic control at busy airports: Tardiness, priorities, equity and violations considerations. Omega, 67, 81–98. doi: https://doi.org/10.1016/j.omega.2016.04.003
  17. Jamili, A. (2017). A robust mathematical model and heuristic algorithms for integrated aircraft routing and scheduling, with consideration of fleet assignment problem. Journal of Air Transport Management, 58, 21–30. doi: https://doi.org/10.1016/j.jairtraman.2016.08.008
  18. Zhang, L., Li, Z., Królczyk, G., Wu, D., Tang, Q. (2019). Mathematical modeling and multi-attribute rule mining for energy efficient job-shop scheduling. Journal of Cleaner Production, 241, 118289. doi: https://doi.org/10.1016/j.jclepro.2019.118289
  19. Correa Issi, G., Linfati, R., Escobar, J. W. (2020). Mathematical Optimization Model for Truck Scheduling in a Distribution Center with a Mixed Service-Mode Dock Area. Journal of Advanced Transportation, 2020, 1–13. doi: https://doi.org/10.1155/2020/8813372
  20. Hammad, A. W., Grzybowska, H., Sutrisna, M., Akbarnezhad, A., Haddad, A. (2019). A novel mathematical optimisation model for the scheduling of activities in modular construction factories. Construction Management and Economics, 38 (6), 534–551. doi: https://doi.org/10.1080/01446193.2019.1682174
  21. Vital-Soto, A., Azab, A., Baki, M. F. (2020). Mathematical modeling and a hybridized bacterial foraging optimization algorithm for the flexible job-shop scheduling problem with sequencing flexibility. Journal of Manufacturing Systems, 54, 74–93. doi: https://doi.org/10.1016/j.jmsy.2019.11.010
  22. Evler, J., Asadi, E., Preis, H., Fricke, H. (2021). Airline ground operations: Schedule recovery optimization approach with constrained resources. Transportation Research Part C: Emerging Technologies, 128, 103129. doi: https://doi.org/10.1016/j.trc.2021.103129
  23. Xia, Q., Xu, S. (2023). Ramified Optimal Transportation with Payoff on the Boundary. SIAM Journal on Mathematical Analysis, 55 (1), 186–209. doi: https://doi.org/10.1137/20m1367714
  24. Ciarlet, P., Kachanovska, M. (2022). A Mathematical Study of a Hyperbolic Metamaterial in Free Space. SIAM Journal on Mathematical Analysis, 54 (2), 2216–2250. doi: https://doi.org/10.1137/21m1404223
  25. Ahmad, H., A. Khan, T., Yao, S.-W. (2020). Numerical solution of second order Painlevé differential equation. Journal of Mathematics and Computer Science, 150–157. doi: https://doi.org/10.22436/jmcs.021.02.06
  26. Agustín, A., Alonso-Ayuso, A., Escudero, L. F., Pizarro, C. (2010). Mathematical optimization models for air traffic flow management: A review. Available at: https://burjcdigital.urjc.es/handle/10115/3405
  27. Bertsimas, D., Patterson, S. S. (2000). The Traffic Flow Management Rerouting Problem in Air Traffic Control: A Dynamic Network Flow Approach. Transportation Science, 34 (3), 239–255. doi: https://doi.org/10.1287/trsc.34.3.239.12300
Математична модель для оптимізації управління розкладом повітряного руху під час пандемії COVID-19

##submission.downloads##

Опубліковано

2023-12-28

Як цитувати

Nasution, D., Mawengkang, H., Fahmi, & Zarlis, M. (2023). Математична модель для оптимізації управління розкладом повітряного руху під час пандемії COVID-19. Eastern-European Journal of Enterprise Technologies, 6(3 (126), 18–26. https://doi.org/10.15587/1729-4061.2023.293514

Номер

Том 6 № 3 (126) (2023): Процеси управління

Розділ

Процеси управління

Ліцензія

Авторське право (c) 2023 Darmeli Nasution, Herman Mawengkang, Fahmi, Muhammad Zarlis

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.