Analytical description of adjustment of rolls for manufacturing parts from elastic sheet material

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.298427

Keywords:

normal curvature, geodesic curvature, sheet part, billet calculation, conical rolls

Abstract

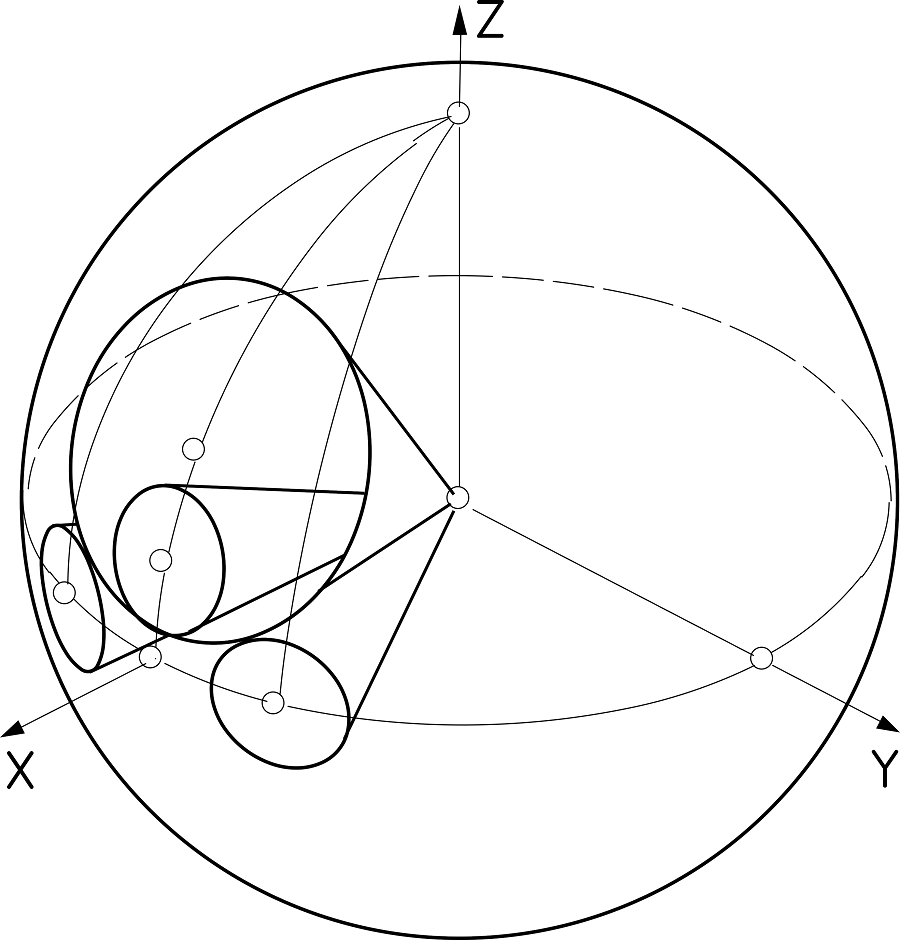
The object of research is the process of bending sheet material, taking into account its springiness. When manufacturing sheet parts by bending from a completely elastic sheet, its shape is completely restored after the deformation stops, unlike an elastic sheet. Thus, when producing cylindrical parts by drawing between three rolls, the resulting radius of the cylindrical part will be larger than the calculated one. This phenomenon is evaluated by the coefficient of springing – the ratio of the calculated radius to the one obtained after partial expansion.

When manufacturing conical parts, this approach cannot be applied, because the value of the radius is variable. The article applies the theory of surface bending from differential geometry. The curvature of the line on the surface has two components - normal and geodesic. When the surface is bent, the normal component changes, while the geodesic component remains unchanged. The magnitude of the normal component depends on the angle between the origin of the cone and its axis. So, for a cone with a base of radius R and an angle of 20°, the normal curvature is 0.94/R, and the geodesic curvature is 0.34/R. For cylindrical parts, the geodesic curvature of the cross-section (circle) is zero, so it is not necessary to take it into account.

Usually, adjustment of rolls for the production of conical parts is carried out experimentally. The difference of the proposed approach lies in the elimination of this problem thanks to the decomposition of the curvature of the base of the cone into two components. This allows to calculate the settings of the rolls and thereby reduce their adjustment time. The parameters of the rolls and their mutual placement are calculated for the production of conical parts of the required size, taking into account their springiness. The field of application of the obtained results is the production of parts by bending flat metal sheet blanks

Author Biographies

Serhii Pylypaka, National University of Life and Environmental Sciences of Ukraine

Doctor of Technical Sciences, Professor, Head of Department

Department of Descriptive Geometry, Engineering and Computer Graphics

Vyacheslav Hropost, National University of Life and Environmental Sciences of Ukraine

Postgraduate Student

Department of Descriptive Geometry, Engineering and Computer Graphics

Tetiana Volina, National University of Life and Environmental Sciences of Ukraine

PhD, Associate Professor

Department of Descriptive Geometry, Engineering and Computer Graphics

Tetiana Kresan, National University of Life and Environmental Sciences of Ukraine

PhD, Associate Professor, Head of Department

Department of Natural, Mathematical and General Engineering Disciplines

Serhii Borodai, Sumy National Agrarian University

Senior Lecturer

Department of Architecture and Surveying Engineering

References

  1. Liu, H., Liu, Y., Zhang, P., Du, X. (2020). Effect of weld zone and corner with cold bending effect on wrinkling of rectangular welded tube in rotary draw bending. Thin-Walled Structures, 157, 107115. https://doi.org/10.1016/j.tws.2020.107115
  2. Schuh, G., Bergweiler, G., Bickendorf, P., Fiedler, F., Colag, C. (2020). Sheet Metal Forming Using Additively Manufactured Polymer Tools. Procedia CIRP, 93, 20–25. https://doi.org/10.1016/j.procir.2020.04.013
  3. Yang, S., Shim, D., Ji, H., Baek, J., Kim, B., Ahn, S., Park, S. (2016). Process Design of Conical Roll-Shaping for Fabrication of Variable Curvature Spiral Blade. Journal of the Korean Society for Precision Engineering, 33 (11), 911–918. https://doi.org/10.7736/kspe.2016.33.11.911
  4. John Panicker, G. (2022). Study on Sheet Metal Bending. ScienceOpen. https://doi.org/10.14293/s2199-1006.1.sor-.pp0xuzu.v1
  5. Semenovskyi, О., Titova, L., Mykhnian, O. (2021). Hardness – volumetric characteristic of material. Naukovij Žurnal «Tehnìka Ta Energetika», 12 (4). https://doi.org/10.31548/machenergy2021.04.139
  6. Kutsenko, A., Kutsenko, O., Yaremenko, V. (2021). On some aspects of implementation of boundary elements method in plate theory. Naukovij Žurnal «Tehnìka Ta Energetika», 12 (3). https://doi.org/10.31548/machenergy2021.03.107
  7. Pylypaka, S., Kresan, Т., Hropost, V., Babka, V., Hryshchenko, I. (2022). Calculation of the bending parameters of a flat workpiece into a twist of a helicoid torso. Naukovij Žurnal «Tehnìka Ta Energetika», 13 (4). https://doi.org/10.31548/machenergy.13(4).2022.81-88
  8. Ikumapayi, O. M., Afolalu, S. A., Kayode, J. F., Kazeem, R. A., Akande, S. (2022). A concise overview of deep drawing in the metal forming operation. Materials Today: Proceedings, 62, 3233–3238. https://doi.org/10.1016/j.matpr.2022.04.221
  9. Trzepieciński, T. (2020). Recent Developments and Trends in Sheet Metal Forming. Metals, 10 (6), 779. https://doi.org/10.3390/met10060779
  10. Nesvidomin, V. M., Pylypaka, T. S., Babka, V. M. (2010). Pat. No. 53688. Sposib vyhotovlennia konichnykh detalei uperedzhenym zghynanniam za dopomohoiu konichnykh valkiv. No. u201005553; declareted: 07.05.2010; published: 11.10.2010, Bul. No. 19. Available at: https://iprop-ua.com/inv/pdf/ns283etl-pub-description.pdf
Analytical description of adjustment of rolls for manufacturing parts from elastic sheet material

Downloads

Published

2024-02-28

How to Cite

Pylypaka, S., Hropost, V., Volina, T., Kresan, T., & Borodai, S. (2024). Analytical description of adjustment of rolls for manufacturing parts from elastic sheet material. Eastern-European Journal of Enterprise Technologies, 1(7 (127), 60–65. https://doi.org/10.15587/1729-4061.2024.298427

Issue

Vol. 1 No. 7 (127) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2024 Serhii Pylypaka, Vyacheslav Hropost, Tetiana Volina, Tetiana Kresan, Serhii Borodai

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.