Construction of homogeneous solutions of the torsion problem for a radially inhomogeneous transversely isotropic cylinder

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.298737

Keywords:

torsion problem, elastic moduli, penetrating solution, boundary layer, torsional moment

Abstract

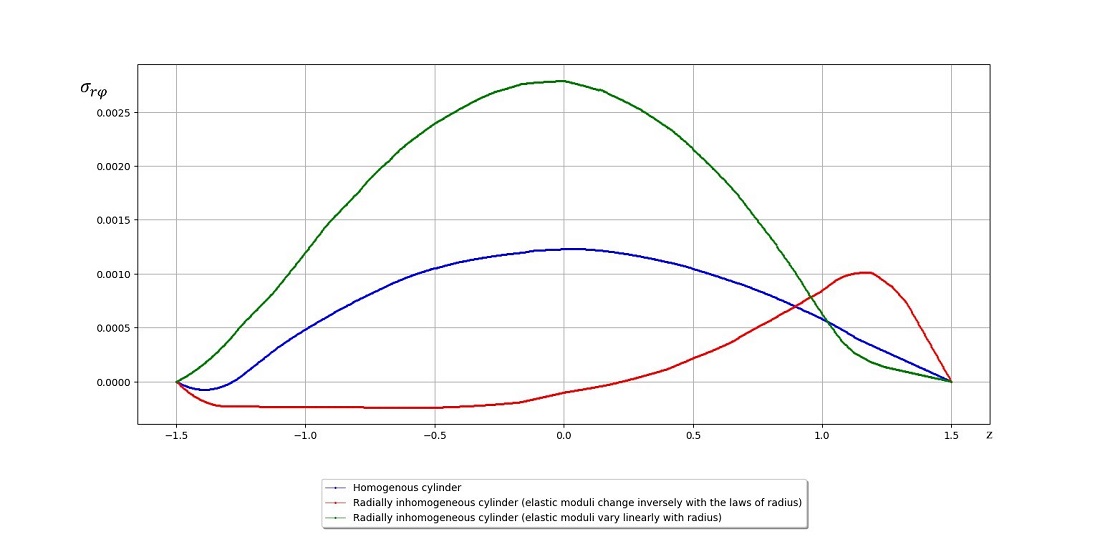
The torsion problem for a radially inhomogeneous transversely isotropic cylinder of small thickness was investigated by the method of asymptotic integration of elasticity theory equations. It is assumed that the side part of the cylinder is stress-free, and boundary conditions are set at the ends of the cylinder, leaving the cylinder in equilibrium. The elastic moduli are thought to be arbitrary continuous functions of the variable along the cylinder radius. The formulated boundary value problem is reduced to a spectral problem containing a small parameter characterizing the thin-walledness of the cylinder. Homogeneous solutions are built, i.e. any solutions of the equilibrium equation satisfying the condition of no stresses on the side surfaces. It is shown that the solution of the torsion problem consists of a penetrating solution and a boundary layer character solution similar to Saint-Venant's edge effect in the theory of inhomogeneous plates. The penetrating solution determines the internal stress-strain state of a radially inhomogeneous cylinder. The stress state determined by the penetrating solution is equivalent to the torsional moments of stresses acting in the cross-section perpendicular to the cylinder axis. Solutions having the boundary layer character are localized at the ends of the cylinder and decrease exponentially with distance from the ends. These solutions are absent in applied shell theories. Asymptotic formulas for displacement and stresses are built, which make it possible to calculate the three-dimensional stress-strain state of a radially inhomogeneous transversely isotropic cylinder of small thickness. Based on the obtained asymptotic expansions, it is possible to assess the applicability of applied theories and build a refined applied theory for radially inhomogeneous cylindrical shells

Author Biography

Natiq Akhmedov, Azerbaijan State University of Economics (UNEC)

Doctor of Mathematics, Professor, Head of Department

Department of Mathematics and Statistics

References

  1. Birman, V., Byrd, L. W. (2007). Modeling and Analysis of Functionally Graded Materials and Structures. Applied Mechanics Reviews, 60 (5), 195–216. https://doi.org/10.1115/1.2777164
  2. Tokovyy, Y., Ma, C.-C. (2019). Elastic Analysis of Inhomogeneous Solids: History and Development in Brief. Journal of Mechanics, 35 (5), 613–626. https://doi.org/10.1017/jmech.2018.57
  3. Sachdeva, C., Padhee, S. S. (2018). Functionally graded cylinders: Asymptotically exact analytical formulations. Applied Mathematical Modelling, 54, 782–802. https://doi.org/10.1016/j.apm.2017.10.019
  4. Lin, H.-C.Dong, S. B. (2006). On the Almansi-Michell Problems for an Inhomogeneous, Anisotropic Cylinder. Journal of Mechanics, 22 (1), 51–57. https://doi.org/10.1017/s1727719100000782
  5. Ieşan, D., Quintanilla, R. (2007). On the deformation of inhomogeneous orthotropic elastic cylinders. European Journal of Mechanics - A/Solids, 26 (6), 999–1015. https://doi.org/10.1016/j.euromechsol.2007.03.004
  6. Grigorenko, A. Ya., Yaremchenko, S. N. (2016). Analysis of the Stress–Strain State of Inhomogeneous Hollow Cylinders. International Applied Mechanics, 52 (4), 342–349. https://doi.org/10.1007/s10778-016-0757-3
  7. Grigorenko, A. Ya Yaremchenko, S. N. (2019). Three-Dimensional Analysis of the Stress–Strain State of Inhomogeneous Hollow Cylinders Using Various Approaches. International Applied Mechanics, 55 (5), 487–494. https://doi.org/10.1007/s10778-019-00970-2
  8. Tutuncu, N., Temel, B. (2009). A novel approach to stress analysis of pressurized FGM cylinders, disks and spheres. Composite Structures, 91 (3), 385–390. https://doi.org/10.1016/j.compstruct.2009.06.009
  9. Jabbari, M., Mohazzab, A. H., Bahtui, A., Eslami, M. R. (2007). Analytical solution for three‐dimensional stresses in a short length FGM hollow cylinder. ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift Für Angewandte Mathematik Und Mechanik, 87 (6), 413–429. https://doi.org/10.1002/zamm.200610325
  10. Akhmedov, N., Akbarova, S. (2021). Behavior of solution of the elasticity problem for a radial inhomogeneous cylinder with small thickness. Eastern-European Journal of Enterprise Technologies, 6 (7 (114)), 29–42. https://doi.org/10.15587/1729-4061.2021.247500
  11. Akhmedov, N. K. (2021). Axisymmetric problem of the elasticity theory for the radially inhomogeneous cylinder with a fixed lateral surface. Journal of Applied and Computational Mechanics, 7 (2), 598–610. Available at: https://jacm.scu.ac.ir/article_15541_f4ed60dbc90a1d5f1ed54fb1ec892658.pdf
  12. Akhmedov, N., Akbarova, S., Ismayilova, J. (2019). Analysis of axisymmetric problem from the theory of elasticity for an isotropic cylinder of small thickness with alternating elasticity modules. Eastern-European Journal of Enterprise Technologies, 2 (7 (98)), 13–19. https://doi.org/10.15587/1729-4061.2019.162153
  13. Ismayilova, J. (2019). Studying elastic equilibrium of a small thickness isotropic cylinder with variable elasticity module. Transactions of NAS of Azerbaycan, 39 (7). Available at: https://transmech.imm.az/upload/articles/Jalala_Ismayilova_Vol_39_8_2019.pdf
  14. Ahmedov, N. K. (1997). Analiz pogranichnogo sloya v osesimmetrichnoy zadache teorii uprugosti dlya radial'no-sloistogo tsilindra i rasprostraneniya osesimmetrichnyh voln. Prikladnaya matematika i mehanika, 61 (5), 863–872.
  15. Mekhtiev, M. F. (2019). Asymptotic Analysis of Spatial Problems in Elasticity. In Advanced Structured Materials. Springer Singapore. https://doi.org/10.1007/978-981-13-3062-9
  16. Lurie, A. I. (1970). Theory of Elasticity. Moscow.
  17. Sadd, M. (2005). Theory, Applications and Numerics. Elsevier.
  18. Lekhnitskii, S. G. (1971). Torsion of Anisotropic and Non-homogeneous Beams. Moscow.
  19. Lekhnitskii, S. G. (1981). Theory of Elasticity of an Anisotropic Body. Moscow. Available at: https://archive.org/details/lekhnitskii-theory-of-elasticity-of-an-anisotropic-body-mir-1981
  20. Ecsedi, I., Baksa, A. (2018). Torsion of functionally graded anisotropic linearly elastic circular cylinder. Engineering Transactions, 66 (4), 413–426. https://doi.org/10.24423/EngTrans.923.20181003
  21. Akhmedov, N. K., Ustinov, Yu. A. (1988). On St. Venant’s principle in the torsion problem for a laminated cylinder. Journal of Applied Mathematics and Mechanics, 52 (2), 207–210. https://doi.org/10.1016/0021-8928(88)90136-0
  22. Akperova, S. B. (2010). Analiz zadachi krucheniya transversal'no-izotropnogo tsilindra maloy tolshchiny s peremennymi modulyami sdviga. Vestnik Donskogo Gosudarstvennogo Tehnicheskogo Universiteta, 10 (5), 634–639.
  23. Mikhlin, S. G. (1977). Partial Linear Equations. Moscow.
  24. Gol'denveyzer, A. L. (1963). Postroenie priblizhennoy teorii izgiba obolochki pri pomoshchi asimptoticheskogo integrirovaniya uravneniy teorii uprugosti. Prikladnaya matematika i mehanika, 27 (4), 593–608.
  25. Akhmedov, N. K., Sofiyev, A. H. (2019). Asymptotic analysis of three-dimensional problem of elasticity theory for radially inhomogeneous transversally-isotropic thin hollow spheres. Thin-Walled Structures, 139, 232–241. https://doi.org/10.1016/j.tws.2019.03.022
  26. Ustinov, Y. (2006). The mathematical theory of transversely non-uniform plates. Rostov-on-Don: OOOTsVVR.
Construction of homogeneous solutions of the torsion problem for a radially inhomogeneous transversely isotropic cylinder

Downloads

Published

2024-02-28

How to Cite

Akhmedov, N. (2024). Construction of homogeneous solutions of the torsion problem for a radially inhomogeneous transversely isotropic cylinder. Eastern-European Journal of Enterprise Technologies, 1(7 (127), 22–29. https://doi.org/10.15587/1729-4061.2024.298737

Issue

Vol. 1 No. 7 (127) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2024 Natiq Akhmedov

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.