Finding an analytical solution for the cylinder’s fluxmetric demagnetizing factor using spherical harmonics

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.301008

Keywords:

cylinder fluxmetric demagnetizing factor, inductive magnetization, spherical harmonics of the magnetic field

Abstract

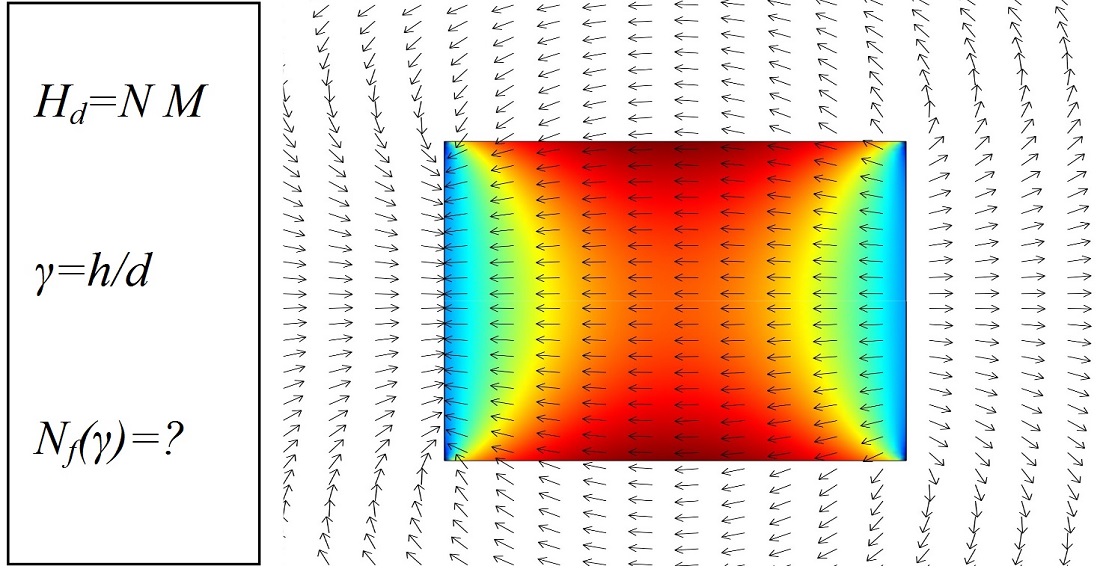
The work examines an analytical solution for calculating the fluxmetric demagnetizing factor of cylindrical magnets at large values of magnetic susceptibility and an arbitrary value of elongation. The application of the analytical solution for calculating the demagnetizing factor significantly simplifies the modeling and calculation of magnetic characteristics of cylindrical technical objects. A simplified analytical model of the scalar potential of the magnetic field of a cylinder with infinite magnetic favorability, inductively magnetized in a uniform magnetic field, was constructed using an approximate representation of the distribution of fictitious magnetic charges on its surface. The method of spherical harmonic analysis for the magnetic field was used, which made it possible to obtain an analytical representation of the demagnetization field in the central cross section of the cylinder. Limitation of the harmonic series of this representation by seven first harmonics is proposed, and an additional amplitude factor is applied to correct the contribution of the first harmonic to the demagnetization field. This made it possible to compensate for the distortion of the magnetic field near the ends of the cylinder and bring the simplified analytical model closer to the target mathematical model with a uniform demagnetization magnetic field. The reliability of the results of calculating the fluxmetric demagnetizing factor according to the derived formula was evaluated by comparing them with the known results obtained using the numerical method of calculation and according to empirical formulas. It is shown that the proposed approach makes it possible to obtain reliable results of calculating the fluxmetric demagnetizing factor with a deviation of up to 5 % at infinite favorability in the range of cylinder elongation values from 0.01 to 500

Author Biographies

Andriy Getman, National Technical University "Kharkiv Polytechnic Institute"

Doctor of Technical Sciences, Senior Researcher

Department of Theoretical Electrical Engineering

Oleksandr Konstantinov, National Technical University "Kharkiv Polytechnic Institute"

Postgtaduate Student

Department of Theoretical Electrical Engineering

References

  1. Rozenblat, M. A. (1954). Koeffitsienty razmagnichivaniya sterzhney vysokoy pronitsaemosti. Zhurnal tehnicheskoy fiziki, 4 (24), 637–661.
  2. Okoshi, T. (1965). Demagnetizing Factors of Rods and Tubes Computed from Analog Measurements. Journal of Applied Physics, 36 (8), 2382–2387. https://doi.org/10.1063/1.1714495
  3. Yamamoto, Y., Yamada, H. (1982). New analytical expressions for flux distribution and demagnetizing factor of cylindrical core. Electrical Engineering in Japan, 102 (3), 1–8. https://doi.org/10.1002/ecja.4391020302
  4. Getman, A. V., Konstantinov, A. V. (2013). Cylindrical harmonics of magnetic field of linear magnetized cylinder. Tecnnical Electrodinamics, 1, 3–8. Available at: http://dspace.nbuv.gov.ua/handle/123456789/62253
  5. Get'man, A. V., Konstantinov, A. V. (2013). Method of cylindrical harmonic analysis of magnetic field of objects with inductive magnetization. Eastern-European Journal of Enterprise Technologies, 3 (5 (63), 3–8. Available at: https://journals.uran.ua/eejet/article/view/14463
  6. Chen, D.-X., Brug, J. A., Goldfarb, R. B. (1991). Demagnetizing factors for cylinders. IEEE Transactions on Magnetics, 27 (4), 3601–3619. https://doi.org/10.1109/20.102932
  7. Varga, L. K., Kováč, J., Novák, L. (2020). Determination of external and internal demagnetizing factors for strip-like amorphous ribbon samples. Journal of Magnetism and Magnetic Materials, 507, 166845. https://doi.org/10.1016/j.jmmm.2020.166845
  8. Kobayashi, M., Ishikawa, Y. (1992). Surface magnetic charge distributions and demagnetizing factors of circular cylinders. IEEE Transactions on Magnetics, 28 (3), 1810–1814. https://doi.org/10.1109/20.141290
  9. Etse, K., Mininger, X. (2022). Determination of demagnetizing factors for various geometries using an iterative numerical approach. Journal of Magnetism and Magnetic Materials, 564, 170151. https://doi.org/10.1016/j.jmmm.2022.170151
  10. Chadebec, O., Rouve, L.-L., Coulomb, J.-L. (2002). New methods for a fast and easy computation of stray fields created by wound rods. IEEE Transactions on Magnetics, 38 (2), 517–520. https://doi.org/10.1109/20.996136
  11. Chen, D.-X., Pardo, E., Sanchez, A. (2006). Fluxmetric and magnetometric demagnetizing factors for cylinders. Journal of Magnetism and Magnetic Materials, 306 (1), 135–146. https://doi.org/10.1016/j.jmmm.2006.02.235
  12. Prozorov, R., Kogan, V. G. (2018). Effective Demagnetizing Factors of Diamagnetic Samples of Various Shapes. Physical Review Applied, 10 (1). https://doi.org/10.1103/physrevapplied.10.014030
  13. Maxwell, J. C. (1998). A Treatise On Electricity And Magnetism. Oxford University Press. https://doi.org/10.1093/oso/9780198503743.001.0001
  14. Smythe, W. (1989). Static and Dynamic Electricity. Hemisphere Publishing Corporation, 623.
  15. Van Bladel, J. G. (2006). Electromagnetic Fields. John Wiley & Sons. https://doi.org/10.1002/047012458x
  16. Vanderlinde, J. (2005). Classical Electromagnetic Theory. Springer Netherlands. https://doi.org/10.1007/1-4020-2700-1
  17. Get'man, A. V., Konstantinov, A. V. (2011). Spatial distribution of charged cylindrical surfaces potential. Eastern-European Journal of Enterprise Technologies, 2 (5 (50), 60–62. Available at: https://journals.uran.ua/eejet/article/view/1794
Finding an analytical solution for the cylinder’s fluxmetric demagnetizing factor using spherical harmonics

Downloads

Published

2024-04-30

How to Cite

Getman, A., & Konstantinov, O. (2024). Finding an analytical solution for the cylinder’s fluxmetric demagnetizing factor using spherical harmonics. Eastern-European Journal of Enterprise Technologies, 2(5 (128), 33–41. https://doi.org/10.15587/1729-4061.2024.301008

Issue

Vol. 2 No. 5 (128) (2024): Applied physics

Section

Applied physics

License

Copyright (c) 2024 Andriy Getman, Oleksandr Konstantinov

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.