Construction of mathematical and computer models for calculating contact characteristics of interaction between a rigid punch and an elastic half-space

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.302792

Keywords:

spatial contact problem, analytical solution, finite-element method, ANSYS, CLIPS

Abstract

The subject of this study is a punch-elastic half-space system under compressive force. The paper solves the problem of determining contact stresses and displacements. The content of results is the constructed models and the assessment of their adequacy.

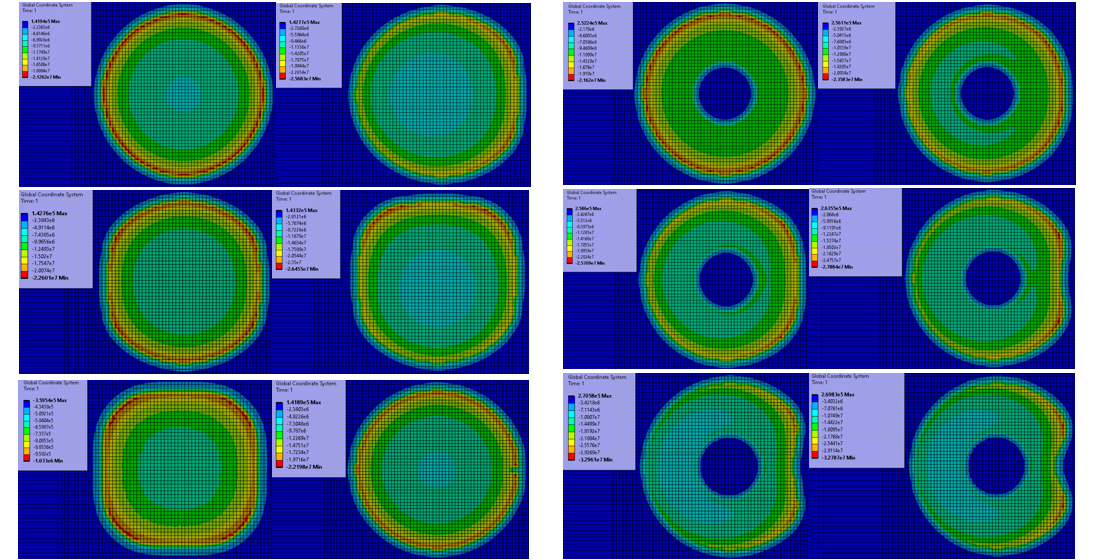
This work considers the problem of pressing a rigid plane double-connected punch on a homogeneous and isotropic elastic half-space. To obtain an analytical solution, a variant of the perturbation method based on the expansion of the potential of a simple layer distributed over a double-connected region by a small parameter was applied. The problem of pressing a flat punch in the form of a non-circular ring is reduced to a sequence of problems for a punch in the form of a circular ring. This allows us to use a known solution for a circular ring.

Finite element models were built using ANSYS. A group of models was constructed to take into account possible damage in the event that the punch-elastic half-space system is exposed to difficult natural conditions or an aggressive environment during a certain time of modeling. A database was formed for the purpose of further transferring it to CLIPS. Sets of rules and knowledge were compiled.

A generalizing algorithm was developed for the problems of constructing and analyzing mathematical and computer models of contact interaction between a rigid cylindrical punch with a flat double-connected base with an elastic half-space under the action of a compressive force. The problem of determining the geometric shape of the cross-section of an annular punch in the plan for the punch-elastic half-space system was solved for the case when the contact zone is not known in advance. The devised approach could be employed in engineering calculations for strength and durability

Author Biographies

Tetyana Zaytseva, Oles Honchar Dnipro National University

PhD, Аssociate Professor, Head of Department

Department of Computer Technologies

Vladyslav Zhushman, Oles Honchar Dnipro National University

Postgraduate Student

Department of Computer Technologies

References

  1. Liu, W. K., Li, S., Park, H. S. (2022). Eighty Years of the Finite Element Method: Birth, Evolution, and Future. Archives of Computational Methods in Engineering, 29 (6), 4431–4453. https://doi.org/10.1007/s11831-022-09740-9
  2. Yilmaz, K. B., Comez, I., Yildirim, B., Güler, M. A., El-Borgi, S. (2018). Frictional receding contact problem for a graded bilayer system indented by a rigid punch. International Journal of Mechanical Sciences, 141, 127–142. https://doi.org/10.1016/j.ijmecsci.2018.03.041
  3. Bonari, J., Marulli, M. R., Hagmeyer, N., Mayr, M., Popp, A., Paggi, M. (2019). A multi-scale FEM-BEM formulation for contact mechanics between rough surfaces. Computational Mechanics, 65 (3), 731–749. https://doi.org/10.1007/s00466-019-01791-3
  4. Gladwell, G. M. L. (Eds.) (2008). Contact Problems – the legacy of L.A. Galin. Springer, 318. https://doi.org/10.1007/978-1-4020-9043-1
  5. Loboda, V., Shevelova, N., Khodanen, T., Lapusta, Y. (2022). An interaction of electrically conductive and electrically permeable collinear cracks in the interface of piezoelectric materials. Archive of Applied Mechanics, 92 (5), 1465–1480. https://doi.org/10.1007/s00419-022-02123-3
  6. Guz, A. N., Zozulya, V. V. (2002). Elastodynamic unilateral contact problems with friction for bodies with crack. International Applied Mechanics, 38 (8), 895–932. https://doi.org/10.1023/a:1021266113662
  7. Myshkin, N. K., Goryacheva, I. G., Grigoriev, A. Ya., Kavaliova, I. N., Makhovskaya, Yu. Yu. (2020). Contact Interaction in Precision Tribosystems. Journal of Friction and Wear, 41 (3), 191–197. https://doi.org/10.3103/s1068366620030113
  8. Li, B., Li, P., Zhou, R., Feng, X.-Q., Zhou, K. (2022). Contact mechanics in tribological and contact damage-related problems: A review. Tribology International, 171, 107534. https://doi.org/10.1016/j.triboint.2022.107534
  9. Roitman, A. B., Shishkanova, S. F. (1973). The solution of the annular punch problem with the aid of recursion relations. Soviet Applied Mechanics, 9 (7), 725–729. https://doi.org/10.1007/bf00882996
  10. Shishkanova, S. F. (1990). Stress state of an elastic half-space weakened by a plane crack which is close to being annular. Soviet Applied Mechanics, 26 (5), 430–435. https://doi.org/10.1007/bf00887257
  11. Shyshkanova, G., Zaуtseva, T., Frydman, O. (2015). The analysis of manufacturing errors effect on contact stresses distribution under the ring parts deformed asymmetrically. Metallurgical and Mining Industry, 7, 352–357. Available at: https://www.metaljournal.com.ua/assets/Journal/english-edition/MMI_2015_7/055Shyshkanova-352-357.pdf
  12. Shyshkanova, G. (2018). About Stability of First Kind Equation Solving. 2018 IEEE First International Conference on System Analysis & Intelligent Computing (SAIC). https://doi.org/10.1109/saic.2018.8516805
  13. Babich, S. Yu., Guz, A. N., Rudnitskii, V. B. (2004). Contact Problems for Prestressed Elastic Bodies and Rigid and Elastic Punches. International Applied Mechanics, 40 (7), 744–765. https://doi.org/10.1023/b:inam.0000046219.34646.4e
  14. Babych, S. Yu., Yarets’ka, N. O. (2021). Contact Problem for an Elastic Ring Punch and a Half-Space with Initial (Residual) Stresses*. International Applied Mechanics, 57 (3), 297–305. https://doi.org/10.1007/s10778-021-01081-7
  15. Yarets’ka, N. (2023). Contact Problems for Cylindrical Stamps and Elastic Bodies with Initial (Residual) Stresses. Advanced Structured Materials, 517–546. https://doi.org/10.1007/978-3-031-37313-8_29
  16. Zare, I., Allen, M. S. (2021). Adapting a contact-mechanics algorithm to predict damping in bolted joints using quasi-static modal analysis. International Journal of Mechanical Sciences, 189, 105982. https://doi.org/10.1016/j.ijmecsci.2020.105982
  17. Wang, F., Wei, H. (2018). Virtual element method for simplified friction problem. Applied Mathematics Letters, 85, 125–131. https://doi.org/10.1016/j.aml.2018.06.002
  18. Shyshkanova, G., Walther, A. (2023). Simple layer potential expansion for optimization of contact interaction taking into account friction and adhesion. Journal of Physics: Conference Series, 2675 (1), 012033. https://doi.org/10.1088/1742-6596/2675/1/012033
  19. Guk, N. A., Obodan, N. I. (2014). An Algorithm for the Solution of the Inverse Problem of the Theory of Shells. Journal of Mathematical Sciences, 198 (2), 192–203. https://doi.org/10.1007/s10958-014-1783-5
  20. Obodan, N. I., Zaitseva, T. A., Fridman, O. D. (2019). Contact Problem for a Rigid Punch and an Elastic Half Space as an Inverse Problem. Journal of Mathematical Sciences, 240 (2), 184–193. https://doi.org/10.1007/s10958-019-04346-2
  21. Shyshkanova, G., Zaytseva, T., Zhushman, V., Levchenko, N., Korotunova, O. (2023). Solving three-dimensional contact problems for foundation design in green building. Journal of Physics: Conference Series, 2609 (1), 012001. https://doi.org/10.1088/1742-6596/2609/1/012001
  22. Free Student Software Downloads. Ansys. Available at: https://www.ansys.com/academic/students?utm_source=ie&utm_medium=video2&utm_campaign=freedownload
  23. Obodan, N., Guk, N., Kozakova, N. (2017). Identification of the additional exposure zone for ensuring a complete contact of the two-layered system. Eastern-European Journal of Enterprise Technologies, 5 (7 (89)), 23–29. https://doi.org/10.15587/1729-4061.2017.109674
  24. Guk, N. A., Kozakova, N. L. (2021). Delamination of a Three-Layer Base Under the Action of Normal Loading. Journal of Mathematical Sciences, 254 (1), 89–102. https://doi.org/10.1007/s10958-021-05290-w
  25. CLIPS. A Tool For Building Expert Systems. Available at: https://www.clipsrules.net/
  26. Banichuk, N. V., Ivanova, S. Yu. (2017). Optimal Structural Design. De Gruyter. https://doi.org/10.1515/9783110531183
  27. Zhou, Y., Lin, Q., Hong, J., Yang, N. (2020). Combined interface shape and material stiffness optimization for uniform distribution of contact stress. Mechanics Based Design of Structures and Machines, 51 (2), 1001–1015. https://doi.org/10.1080/15397734.2020.1860086
  28. Kress, R. (1989). Tikhonov Regularization. Applied Mathematical Sciences, 243–258. https://doi.org/10.1007/978-3-642-97146-4_16
  29. Gutman, E. M. (1994). Mechanochemistry of Solid Surfaces. World Scientific. https://doi.org/10.1142/2373
  30. Dolinskiy, V. M. (1975). Izgib tonkih plastin, podverzhennyh korrozionnomu iznosu. Dinamika i prochnost' mashin, 21, 43–49.
Construction of mathematical and computer models for calculating contact characteristics of interaction between a rigid punch and an elastic half-space

Downloads

Published

2024-04-30

How to Cite

Zaytseva, T., & Zhushman, V. (2024). Construction of mathematical and computer models for calculating contact characteristics of interaction between a rigid punch and an elastic half-space. Eastern-European Journal of Enterprise Technologies, 2(7 (128), 67–78. https://doi.org/10.15587/1729-4061.2024.302792

Issue

Vol. 2 No. 7 (128) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2024 Tetyana Zaytseva, Vladyslav Zhushman

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.