Development of a general algorithm for solving the stability problem of anisotropic plates
DOI:
https://doi.org/10.15587/1729-4061.2024.302838Keywords:
structural stability, plate stability, plate strength, anisotropic plates, orthotropic plates, discretization methodAbstract
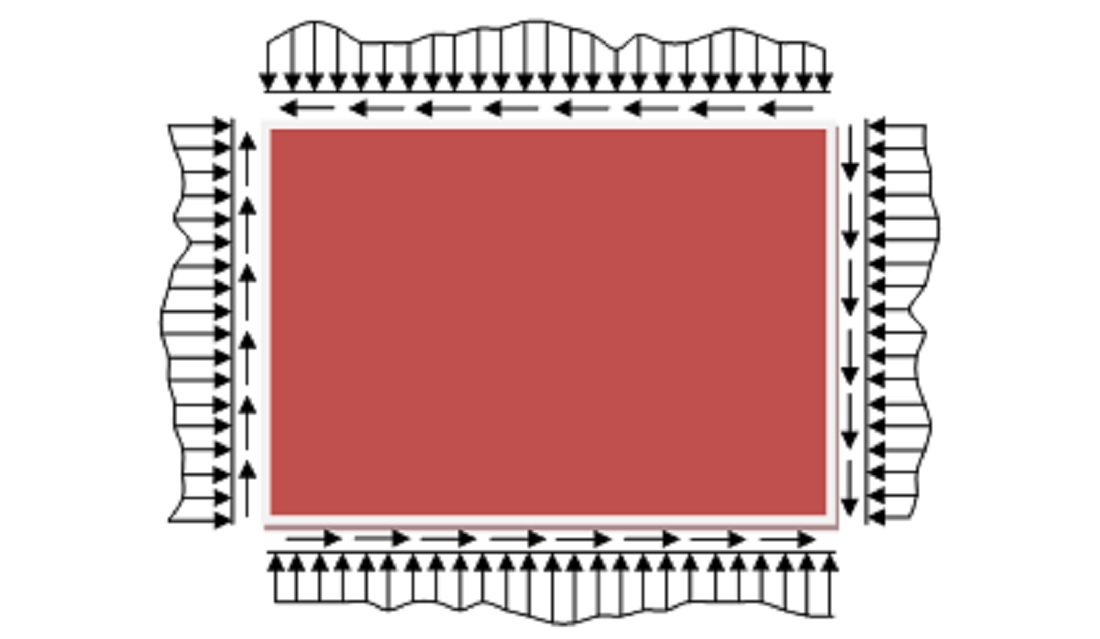
This paper is devoted to the development of general algorithm for solving to the stability problem of anisotropic plates using the additional load discretization method. The study of the stability problem is relevant for all types of structural elements and machine parts, and its importance is especially increasing with respect to anisotropic thin plates. This is due to the fact that with the use of new structures and materials, the material intensity is reduced, the area of application of thin-walled systems with low stiffness, for which the danger of elastic loss of stability increases, and, therefore, the importance and relevance of the theory and methods of practical solution of problems of elastic stability of such structures increases.
In many works, analytical expressions for determination of critical load are given. At present, the determination of critical loads causes great difficulties in their numerical determination. Therefore, the article presents the most effective numerical and analytical solution of this problem.
As a rule, to solve stability problems of anisotropic plates, different representations of the bending deflection function in different rows are used. But the use of such representations is justified only under certain boundary conditions and under the condition of uniformly distributed load. The study described in this paper offers a way to overcome these difficulties, allowing the numerical values of critical forces to be determined without much difficulty. With increasing grid density, the accuracy of the critical load value increases rapidly and with an 8×8 grid, the deviation from the exact solution equal to is 1 %.
From a practical point of view, the discovered mechanism of numerical realization of this problem allows to improve engineering design calculations of stability of anisotropic plates with different conditions on supports and with different loading
References
- Alfutov, N. A. (1991). Osnovy rascheta na ustoychivost’ uprugih sistem. Moscow: Mashinostroyeniye, 336.
- Vol’mir, A. S. (1967). Ustoychivost’ deformiruyemyh sistem. Moscow: Nauka, 984.
- Vinokurov, L. P., Guliyev, Sh. M. (1980). Diskretizatsiya zadachi ustoychivosti ravnovesiya krivyh sterzhney proizvol’nogo ochertaniya. Jurnal Izvestiya vuzov. Stroitel’stvo i arhitektura, 9, 76–79.
- Guliyev, Sh. M. (2021). Resheniye nekotoryh zadach ustoychivosti uprugih sistem po metodu diskretizatsii dobavochnoy nagruzki. Materialy mezhdunarodnoy nauchno-prakticheskoy konferentsii “Osnovniye problemy reytinga vuzov”. Chast’ 2. Gyandja, 12–13.
- Guliyev, Sh. M., Shukurov, R. E. (2023). Resheniye zadachi ustoychivosti sterzhney pri uchete kontakta s uprugim osnovaniyem. Materialy mezhdunarodnoy nauchno-prakticheskoy konferentsii “Chetvertaya promyshlennaya revolyutsiya i innovativnyye tehnologii”. Chast’ 2. Gyandja, 295–296.
- Oreshko, E. I., Erasov, V. S., Lutsenko, A. N. (2016). Calculation features of cores and plates stability. Aviation Materials and Technologies, 4, 74–79. https://doi.org/10.18577/2071-9140-2016-0-4-74-79
- Oreshko, E. I., Erasov, V. S., Podjivotov, N. Yu., Lutsenko, A. N. (2016). Raschet na prochnost’ gibridnoy paneli kryla na baze listov i profiley iz vysokoprochnogo alyuminiy-litiyevogo splava i sloistogo alyumostekloplastika. Aviatsionniye materialy i tehnologii, 1 (40), 53–61.
- Ahajanov, S. B., Myrzabek, D. V. (2020). Raschet na ustoychivost’ pryamougol’noy izotropnoy plastiny. Vestnik Kazahstansko-Britanskogo tehnicheskogo Universiteta, 17 (3), 113–118.
- Ivanov, S. P., Ivanov, O. G., Ivanova, A. S. (2017). The stability of plates under the action of shearing loads. Structural Mechanics of Engineering Constructions and Buildings, 6, 68–73. https://doi.org/10.22363/1815-5235-2017-6-68-73
- Kolpak, E. P., Mal’tseva, L. S. (2015). Ob ustoychivosti szhatyh plastin. Molodoy uchenyy, 14 (94), 1–8. Available at: https://moluch.ru/archive/94/21188
- Kolmogorov, G. A., Ziborova, E. O. (2015). Voprosy ustoychivocti anizotropnyh plastin. Stroitel’naya mehanika inzhenernyh konstruktsiy i sooruzheniy, 2, 63–68.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Shahin Guliyev, Rizvan Shukurov, Hajar Huseynzade, Aliyar Hasanov, Leila Huseynova

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









