Improving safety criteria for transporting hazardous goods by road through optimizing the geometric parameters of their stowage

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.307235

Keywords:

road transportation, voxel-based stowage model, fractal dimensionality, cargo fastening, transportation safety

Abstract

The object of research is the process of cargo transportation by road. The problem of efficient loading and securing of hazardous goods in box containers during their transportation by road is considered.

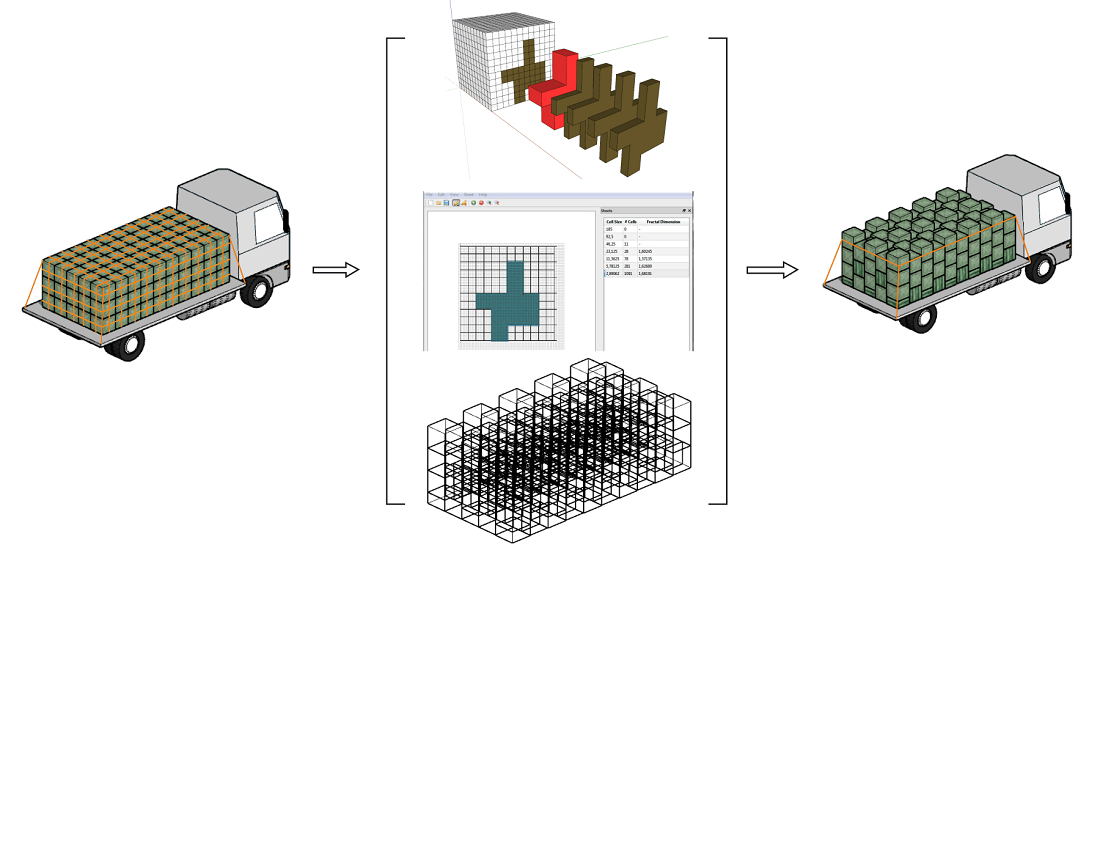
The basic principles of the voxel-based interpretation of the model of loading box containers on road transport are presented, and a general principle for calculating the fractal dimension of such three-dimensional objects has been developed. The calculation is based on the procedure of reducing the dimensionality of space by cutting the object into separate layers and determining the fractal dimensionality of two-dimensional slices. The proposed principle could be used to estimate the fractal dimension of three-dimensional objects in practical tasks in any industry.

A method for simplified calculation of fractal characteristics of three-dimensional bill of lading models of cargo stowage has been devised. The method is based on the assessment of the quality of blocking of the constituent elements of the spatial system in three coordinate directions by the fractal dimension of two-dimensional images of their frames. The method provides opportunities for calculating the quantitative characteristics of the quality of cargo stowage from the standpoint of its transportation safety.

A method for fractal stowing of goods in box containers on a truck platform has been proposed. This method of fractal stowage provides for the absence of slippage and displacement of boxes in the package and makes it impossible for them to overturn in extreme situations. The use of the fractal stowage method allows for an efficient and low-cost technology of securing the cargo as it involves only a circular bandage of the top layer of the loaded package of boxes and its fastening to the vehicle platform at four points

Author Biographies

Serhii Pustiulha, Lutsk National Technical University

Doctor of Technical Sciences, Professor

Department of Architecture and Design

Volodymyr Samchuk, Lutsk National Technical University

PhD, Associate Professor

Department of Building and Civil Engineering

Valentyn Prydiuk, Lutsk National Technical University

PhD, Associate Professor

Department of Automobile and Transport Technology

Oksana Pasichnyk, Lutsk National Technical University

PhD, Associate Professor

Department of Architecture and Design

Oleksandr Shymchuk, Lutsk National Technical University

PhD, Associate Professor

Department of Building and Civil Engineering

References

  1. Popov, O., Iatsyshyn, A., Pecheny, V., Kovach, V., Kovalenko, V. (2023). Approaches to Assessing Consequences of Accidents During Transportation of Hazardous Substances by Road. Studies in Systems, Decision and Control, 327–342. https://doi.org/10.1007/978-3-031-22500-0_22
  2. Guo, J., Luo, C. (2022). Risk assessment of hazardous materials transportation: A review of research progress in the last thirty years. Journal of Traffic and Transportation Engineering (English Edition), 9 (4), 571–590. https://doi.org/10.1016/j.jtte.2022.01.004
  3. Bęczkowska, S. (2019). The method of optimal route selection in road transport of dangerous goods. Transportation Research Procedia, 40, 1252–1259. https://doi.org/10.1016/j.trpro.2019.07.174
  4. Menoni, S. (2007). Transportation Of Dangerous Goods. NATO Science for Peace and Security Series C: Environmental Security, 97–110. https://doi.org/10.1007/978-1-4020-6385-5_6
  5. ADR 2023 - Agreement concerning the International Carriage of Dangerous Goods by Road. Available at: https://unece.org/transport/standards/transport/dangerous-goods/adr-2023-agreement-concerning-international-carriage
  6. Kurpel, D. V., Scarpin, C. T., Pécora Junior, J. E., Schenekemberg, C. M., Coelho, L. C. (2020). The exact solutions of several types of container loading problems. European Journal of Operational Research, 284 (1), 87–107. https://doi.org/10.1016/j.ejor.2019.12.012
  7. Bortfeldt, A., Wäscher, G. (2013). Constraints in container loading – A state-of-the-art review. European Journal of Operational Research, 229 (1), 1–20. https://doi.org/10.1016/j.ejor.2012.12.006
  8. Conca, A., Ridella, C., Sapori, E. (2016). A Risk Assessment for Road Transportation of Dangerous Goods: A Routing Solution. Transportation Research Procedia, 14, 2890–2899. https://doi.org/10.1016/j.trpro.2016.05.407
  9. Junqueira, L., Morabito, R., Sato Yamashita, D. (2012). Three-dimensional container loading models with cargo stability and load bearing constraints. Computers & Operations Research, 39 (1), 74–85. https://doi.org/10.1016/j.cor.2010.07.017
  10. Lim, A., Ma, H., Qiu, C., Zhu, W. (2013). The single container loading problem with axle weight constraints. International Journal of Production Economics, 144 (1), 358–369. https://doi.org/10.1016/j.ijpe.2013.03.001
  11. European Commission, Directorate-General for Mobility and Transport, (2014). Cargo securing for road transport : 2014 European best practices guidelines, Publications Office. https://doi.org/10.2832/80373
  12. Pankratov, A., Romanova, T., Litvinchev, I. (2020). Packing Oblique 3D Objects. Mathematics, 8 (7), 1130. https://doi.org/10.3390/math8071130
  13. Chekanin, V. (2020). Solving the Problem of Packing Objects of Complex Geometric Shape into a Container of Arbitrary Dimension. Proceedings of the 30th International Conference on Computer Graphics and Machine Vision (GraphiCon 2020). Part 2, paper50-1-paper50-13. https://doi.org/10.51130/graphicon-2020-2-3-50
  14. Pustiulha, S., Samostian, V., Tolstushko, N., Korobka, S., Babych, M. (2017). Fractal diagnostics of the degree of fuel atomization by diesel engine injectors. Eastern-European Journal of Enterprise Technologies, 6 (8 (90)), 40–46. https://doi.org/10.15587/1729-4061.2017.116104
  15. Pustiulha, S., Holovachuk, I., Samchuk, V., Samostian, V., Prydiuk, V. (2019). Improvement of the Technology of Tribostate Application of Powder Paints Using Fractal Analysis of Spray Quality. Advances in Design, Simulation and Manufacturing II, 280–289. https://doi.org/10.1007/978-3-030-22365-6_28
  16. Pustiulha, S., Samchuk, V., Samostian, V., Prydiuk, V., Dembitskij, V. (2022). Influence of the City Transport Route Network Discrete Model Geometrical Parameters on a Quality of a Passenger Traffic System Operation. Lecture Notes in Networks and Systems, 740–751. https://doi.org/10.1007/978-3-031-20141-7_66
  17. Feder, J. (1988). Fractals. Springer US. Springer. https://doi.org/10.1007/978-1-4899-2124-6
  18. Mandelbrot, B. B. (1983). The fractal geometry of nature. Henry Holt and Company, 468.
  19. Pustiulha, S., Samchuk, V., Holovachuk, I., Lelyk, I., Klak, Y. (2022). Discrete-voxel representation of object models for the identification and calculation of their fractal parameters. Applied Geometry and Engineering Graphics, 103, 185–200. Available at: http://ageg.knuba.edu.ua/article/view/273596
  20. Zlatanova, S., Ren, F., Xu, Y., Laefer, D. (2024). Editorial: Voxel-based modelling of natural and man-made objects. International Journal of Applied Earth Observation and Geoinformation, 128, 103713. https://doi.org/10.1016/j.jag.2024.103713
Improving safety criteria for transporting hazardous goods by road through optimizing the geometric parameters of their stowage

Downloads

Published

2024-06-29

How to Cite

Pustiulha, S., Samchuk, V., Prydiuk, V., Pasichnyk, O., & Shymchuk, O. (2024). Improving safety criteria for transporting hazardous goods by road through optimizing the geometric parameters of their stowage. Eastern-European Journal of Enterprise Technologies, 3(3 (129), 74–84. https://doi.org/10.15587/1729-4061.2024.307235

Issue

Vol. 3 No. 3 (129) (2024): Control processes

Section

Control processes

License

Copyright (c) 2024 Serhii Pustiulha, Volodymyr Samchuk, Valentyn Prydiuk, Oksana Pasichnyk, Oleksandr Shymchuk

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.