Construction of mathematical models of thermal conductivity for modern electronic devices with elements of a layered structure
DOI:
https://doi.org/10.15587/1729-4061.2024.309346Keywords:
temperature field, thermal conductivity of material, thermal resistance of structures, thermosensitive material, thermally active surfaceAbstract
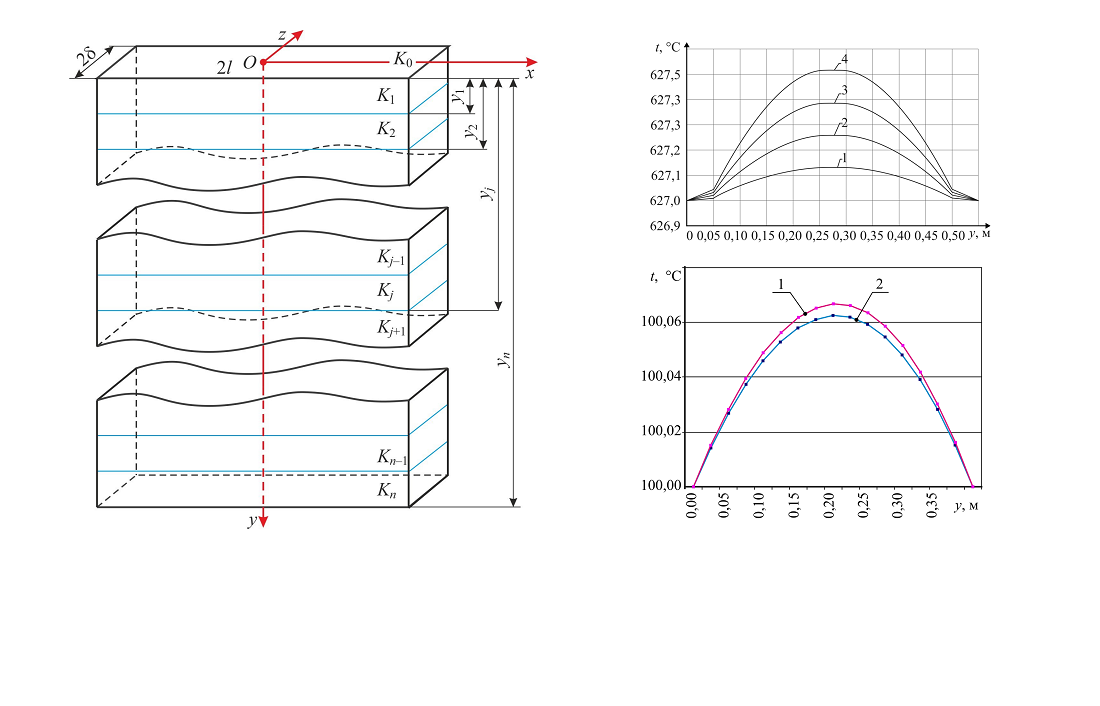
This paper considers a heat conduction process for isotropic layered media with internal thermal heating. As a result of the heterogeneity of environments, significant temperature gradients arise as a result of the thermal load. In order to establish the temperature regimes for the effective operation of electronic devices, linear and non-linear mathematical models for determining the temperature field have been constructed, which would make it possible to further analyze the temperature regimes in these heat-active environments. The coefficient of thermal conductivity for the above structures was represented as a whole using asymmetric unit functions. As a result, the conditions of ideal thermal contact were automatically fulfilled on the surfaces of the conjugation of the layers. This leads to solving one heat conduction equation with discontinuous and singular coefficients and boundary conditions at the boundary surfaces of the medium. For linearization of nonlinear boundary value problems, linearizing functions were introduced. Analytical solutions to both linear and nonlinear boundary value problems were derived in a closed form. For heat-sensitive environments, as an example, the linear dependence of the coefficient of thermal conductivity of structural materials on temperature, which is often observed when solving many practical problems, was chosen. As a result, analytical relations for determining the temperature distribution in these environments were obtained. Based on this, a numerical experiment was performed, and it was geometrically represented depending on the spatial coordinates. This proves that the constructed linear and nonlinear mathematical models testify to their adequacy to the real physical process. They make it possible to analyze heat-active media regarding their thermal resistance. As a result, it becomes possible to increase it and protect it from overheating, which can cause the destruction of not only individual nodes and their elements but also the entire structure
References
- Havrysh, V. I. (2021). Mathematical Models of the Temperature Field in Heat-sensitive Elements of Electronic Devices. Electronic modeling, 43 (6), 19–33. https://doi.org/10.15407/emodel.43.06.019
- Shevchuk, V. A. (2024). Methodology of Investigations of the Thermal Stressed State of Bodies with Thin Multilayer Coatings. Journal of Mathematical Sciences, 278 (5), 780–794. https://doi.org/10.1007/s10958-024-06961-0
- Protsiuk, B. V. (2023). Nonstationary Problems of Heat Conduction for a Thermosensitive Plate with Nonlinear Boundary Condition on One Surface. Journal of Mathematical Sciences, 272 (1), 135–150. https://doi.org/10.1007/s10958-023-06405-1
- Zhuravchak, L. M., Zabrodska, N. V. (2020). Using of partly-boundary elements as a version of the indirect near-boundary element method for potential field modeling. Mathematical Modeling and Computing, 8 (1), 1–10. https://doi.org/10.23939/mmc2021.01.001
- Zhuravchak, L. (2019). Mathematical Modelling of Non-stationary Processes in the Piecewise-Homogeneous Domains by Near-Boundary Element Method. Advances in Intelligent Systems and Computing, 64–77. https://doi.org/10.1007/978-3-030-33695-0_6
- Zhao, Y., Zhou, J., Guo, M., Xu, Y. (2024). Equivalent thin-layer temperature field model (ETTM) for bolted rotors to describe interface temperature jump. International Journal of Heat and Mass Transfer, 222, 125086. https://doi.org/10.1016/j.ijheatmasstransfer.2023.125086
- Breukelman, H. J., Santofimia, M. J., Hidalgo, J. (2023). Dataset of a thermal model for the prediction of temperature fields during the creation of austenite/martensite mesostructured materials by localized laser treatments in a Fe-Ni-C alloy. Data in Brief, 48, 109110. https://doi.org/10.1016/j.dib.2023.109110
- Zhang, W., Wu, M., Du, S., Chen, L., Hu, J., Lai, X. (2023). Modeling of Steel Plate Temperature Field for Plate Shape Control in Roller Quenching Process. IFAC-PapersOnLine, 56 (2), 6894–6899. https://doi.org/10.1016/j.ifacol.2023.10.493
- Filipov, S. M., Faragó, I., Avdzhieva, A. (2023). Mathematical Modelling of Nonlinear Heat Conduction with Relaxing Boundary Conditions. Lecture Notes in Computer Science, 146–158. https://doi.org/10.1007/978-3-031-32412-3_13
- Evstatieva, N., Evstatiev, B. (2023). Modelling the Temperature Field of Electronic Devices with the Use of Infrared Thermography. 2023 13th International Symposium on Advanced Topics in Electrical Engineering (ATEE). https://doi.org/10.1109/atee58038.2023.10108375
- Liu, H., Yu, J., Wang, R. (2023). Dynamic compact thermal models for skin temperature prediction of portable electronic devices based on convolution and fitting methods. International Journal of Heat and Mass Transfer, 210, 124170. https://doi.org/10.1016/j.ijheatmasstransfer.2023.124170
- Bianco, V., De Rosa, M., Vafai, K. (2022). Phase-change materials for thermal management of electronic devices. Applied Thermal Engineering, 214, 118839. https://doi.org/10.1016/j.applthermaleng.2022.118839
- Mathew, J., Krishnan, S. (2021). A Review On Transient Thermal Management of Electronic Devices. Journal of Electronic Packaging. https://doi.org/10.1115/1.4050002
- Zhou, K., Ding, H., Steenbergen, M., Wang, W., Guo, J., Liu, Q. (2021). Temperature field and material response as a function of rail grinding parameters. International Journal of Heat and Mass Transfer, 175, 121366. https://doi.org/10.1016/j.ijheatmasstransfer.2021.121366
- Zhang, Q., Song, H., Gao, C. (2023). The 3-D problem of temperature and thermal flux distribution around defects with temperature-dependent material properties. Thermal Science, 27 (5 Part B), 3903–3920. https://doi.org/10.2298/tsci221003028z
- Song, H., Song, K., Gao, C. (2019). Temperature and thermal stress around an elliptic functional defect in a thermoelectric material. Mechanics of Materials, 130, 58–64. https://doi.org/10.1016/j.mechmat.2019.01.008
- Havrysh, V., Kochan, V. (2023). Mathematical Models to Determine Temperature Fields in Heterogeneous Elements of Digital Devices with Thermal Sensitivity Taken into Account. 2023 IEEE 12th International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS). https://doi.org/10.1109/idaacs58523.2023.10348875
- Havrysh, V. I., Kolyasa, L. I., Ukhanska, O. M., Loik, V. B. (2019). Determination of temperature field in thermally sensitive layered medium with inclusions. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu, 1, 76–82. https://doi.org/10.29202/nvngu/2019-1/5
- Havrysh, V., Ovchar, I., Baranetskyj, J., Pelekh, J., Serduik, P. (2017). Development and analysis of mathematical models for the process of thermal conductivity for piecewise uniform elements of electronic systems. Eastern-European Journal of Enterprise Technologies, 1 (5 (85)), 23–33. https://doi.org/10.15587/1729-4061.2017.92551
- Havrysh, V. I., Kosach, A. I. (2012). Boundary-value problem of heat conduction for a piecewise homogeneous layer with foreign inclusion. Materials Science, 47 (6), 773–782. https://doi.org/10.1007/s11003-012-9455-4
- Gavrysh, V., Tushnytskyy, R., Pelekh, Y., Pukach, P., Baranetskyi, Y. (2017). Mathematical model of thermal conductivity for piecewise homogeneous elements of electronic systems. 2017 14th International Conference The Experience of Designing and Application of CAD Systems in Microelectronics (CADSM). https://doi.org/10.1109/cadsm.2017.7916146
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Vasyl Havrysh, Elvira Dzhumelia, Stepan Kachan, Viktoria Maikher, Ihor Rabiichuk

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









