Devising an analytical method for solving the eighth-order Kolmogorov equations for an asymmetric Markov chain
DOI:
https://doi.org/10.15587/1729-4061.2024.312971Keywords:
state graph, state probabilities, simulation of random processes, distribution of rootsAbstract
The object of research is a complex system of three subsystems, which function independently of each other and are in a working or failed state. There is a need to analytically model and manage the Markov random process in the system, varying the intensity of their development-restoration and degradation-destruction flows. In the study, an analytical method for solving Kolmogorov equations of the eighth order for an asymmetric Markov chain was devised.
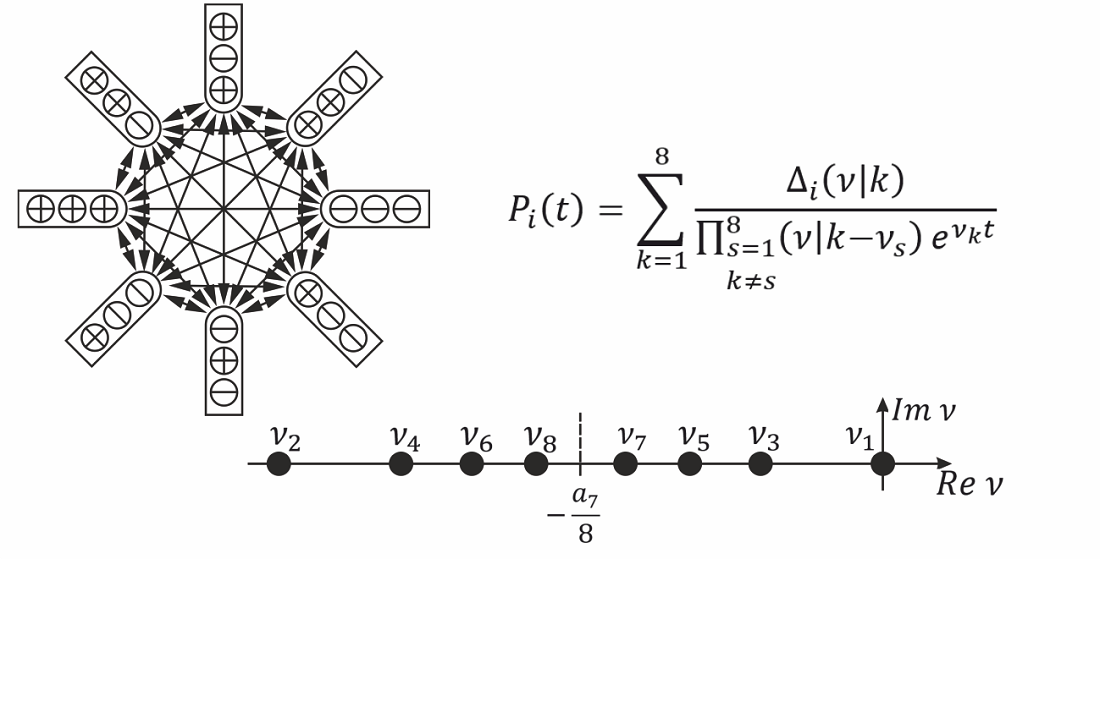
The corresponding Kolmogorov equations of the eighth order have an ordered transition probability matrix. The distribution of the eight roots of this equation in the complex plane has central symmetry.
The results are analytical solutions for the probabilities of the eight states of the Markov chain in time in the form of ordered determinants with respect to the indices of the eight roots and the indices of the eight states, including the column vector of the initial conditions.
Symmetry has been established in the distribution on the complex plane of eight real, negative roots of the characteristic Kolmogorov equation centered at the point defined as Re ϑ = –a7/8, where a7 is the coefficient of the characteristic equation of the eighth degree at the seventh power. Formulas expressing eight roots of the characteristic Kolmogorov equation have been heuristically derived, one of which is zero, due to the intensities of failures and recovery of three subsystems, the eight states of which in general make up an asymmetric Markov chain.
For structures consisting of three independently functioning processes, the random process of the transition of the structure through eight possible states with a known initial state is determined in time. An analytical solution to Kolmogorov differential equations of the eighth order for an asymmetric state graph is proposed in harmonic form for the purpose of analysis and synthesis of a random Markov process in a triple system.
References
- Hajek, B. (2015). Random Processes for Engineers. Cambridge University Press. https://doi.org/10.1017/cbo9781316164600
- Asmussen, S. (2008). Applied Probability and Queues. Springer Science & Business Media. Available at: https://books.google.co.uk/books?id=X1CacQAACAAJ&pg=PR1&hl=ru&source=gbs_selected_pages&cad=1#v=onepage&q&f=false
- Pender, J. (2014). Nonstationary loss queues via cumulant moment approximations. Probability in the Engineering and Informational Sciences, 29 (1), 27–49. https://doi.org/10.1017/s0269964814000205
- Seabrook, E., Wiskott, L. (2023). A Tutorial on the Spectral Theory of Markov Chains. Neural Computation, 35 (11), 1713–1796. https://doi.org/10.1162/neco_a_01611
- Chen, X., Li, L., Shi, Q. (2015). Stochastic Evolutions of Dynamic Traffic Flow. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-44572-3
- Sadeghian, P., Han, M., Håkansson, J., Zhao, M. X. (2024). Testing feasibility of using a hidden Markov model on predicting human mobility based on GPS tracking data. Transportmetrica B: Transport Dynamics, 12 (1). https://doi.org/10.1080/21680566.2024.2336037
- Kravets, V. V., Kravets, Vl. V., Burov, О. V. (2016). Reliability of Systems. Part 2. Dynamics of Failures. Saarbrucken: Lap lambert Academic Publishing.
- Kravets, V. V., Bass, K. M., Kravets, V. V., Tokar, L. A. (2014). Analytical Solution of Kolmogorov Equations for Four-Condition Homogenous, Symmetric and Ergodic System. Open Journal of Applied Sciences, 04 (10), 497–500. https://doi.org/10.4236/ojapps.2014.410048
- Kravets, V., Kravets, V., Burov, O. (2021). Analytical Modeling of the Dynamic System of the Fourth Order. Transactions on Machine Learning and Artificial Intelligence, 9 (3), 14–24. https://doi.org/10.14738/tmlai.93.9947
- Domanskyi, I. V. (2016). Osnovy enerhoefektyvnosti elektrychnykh system z tiahovymy navantazhenniamy. Kharkiv: TOV «Tsentr informatsiyi transportu Ukrainy», 224. Available at: http://library.kpi.kharkov.ua/files/new_postupleniya/oceesi.pdf
- Kapitsa, M. I., Hryshechkina, T. S. (2014). Rational recovery model of depot processing equipment at the industrial enterprise. Science and Transport Progress, 4 (52), 60–66. https://doi.org/10.15802/stp2014/27319
- Yun, M., Qin, W., Yang, X., Liang, F. (2019). Estimation of urban route travel time distribution using Markov chains and pair-copula construction. Transportmetrica B: Transport Dynamics, 7 (1), 1521–1552. https://doi.org/10.1080/21680566.2019.1637798
- Suliankatchi Abdulkader, R., Deneshkumar, V., Senthamarai Kannan, K., Koyilil, V., Paes, A. T., Sebastian, T. (2021). An application of Markov chain modeling and semi-parametric regression for recurrent events in health data. Communications in Statistics: Case Studies, Data Analysis and Applications, 8 (1), 68–80. https://doi.org/10.1080/23737484.2021.1973926
- Ray, S. N., Bose, S., Chattopadhyay, S. (2020). A Markov chain approach to the predictability of surface temperature over the northeastern part of India. Theoretical and Applied Climatology, 143 (1-2), 861–868. https://doi.org/10.1007/s00704-020-03458-z
- Domanskyi, V., Domanskyi, I., Zakurdai, S., Liubarskyi, D. (2022). Development of technologies for selecting energy-efficient power supply circuits of railway traction networks. Technology Audit and Production Reserves, 4 (1 (66)), 47–54. https://doi.org/10.15587/2706-5448.2022.263961
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Victor Kravets, Mykhailo Kapitsa, Illia Domanskyi, Volodymyr Kravets, Tatiana Hryshechkina, Svitlana Zakurday

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









