Розробка аналітичного методу розв'язання рівнянь Колмогорова восьмого порядку для асиметричного ланцюга Маркова
DOI:
https://doi.org/10.15587/1729-4061.2024.312971Ключові слова:
граф станів, ймовірності станів, моделювання випадкових процесів, розподіл коренівАнотація
Об'єктом дослідження є комплексна система трьох підсистем, які функціонують незалежно одна від другої та перебувають в працездатному або відмовному стані. Виникає необхідність аналітично моделювати та керувати марковським випадковим процесом у системі, варіюючи інтенсивність їх потоків розвитку-відновлення та деградації-руйнування. У дослідженні (розроблено аналітичний метод розв'язання рівнянь Колмогорова восьмого порядку для асиметричного ланцюга Маркова.
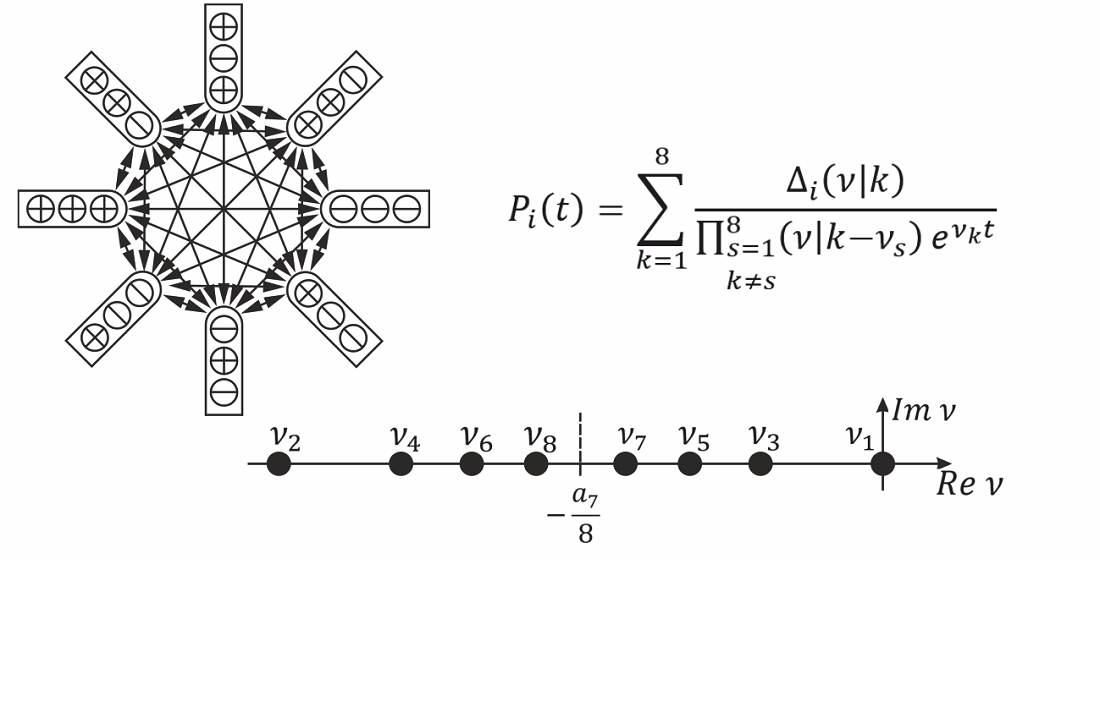
Відповідні рівняння Колмогорова восьмого порядку мають упорядковану матрицю перехідних ймовірностей. Розподіл восьми коренів цього рівняння в комплексній площині має центральну симетрію.
Результатами є аналітичні рішення для ймовірностей восьми станів ланцюга Маркова в часі у формі упорядкованих визначників відносно індексів восьми коренів та індексів восьми станів, включаючи вектор-стовпець початкових умов.
Встановлена симетрія в розподілі на комплексній площині восьми дійсних, від'ємних коренів характеристичного рівняння Колмогорова з центром у точці, визначеній як: , де a7 – коефіцієнт характеристичного рівняння восьмого ступеня при сьомому ступені. Евристично знайдено формули, що виражають вісім коренів характеристичного рівняння Колмогорова, один із яких є нульовим, через інтенсивності відмов і відновлень трьох підсистем, вісім станів яких загалом складають асиметричний ланцюг Маркова.
Для структур, що складаються з трьох незалежно функціонуючих процесів, визначається у часі випадковий процес переходу структури через вісім можливих станів за відомого початкового стану. Запропоновано в гармонійній формі аналітичне розв'язання диференціальних рівнянь Колмогорова восьмого порядку для асиметричного графа станів з метою аналізу та синтезу випадкового процесу марковського в triple system
Посилання
- Hajek, B. (2015). Random Processes for Engineers. Cambridge University Press. https://doi.org/10.1017/cbo9781316164600
- Asmussen, S. (2008). Applied Probability and Queues. Springer Science & Business Media. Available at: https://books.google.co.uk/books?id=X1CacQAACAAJ&pg=PR1&hl=ru&source=gbs_selected_pages&cad=1#v=onepage&q&f=false
- Pender, J. (2014). Nonstationary loss queues via cumulant moment approximations. Probability in the Engineering and Informational Sciences, 29 (1), 27–49. https://doi.org/10.1017/s0269964814000205
- Seabrook, E., Wiskott, L. (2023). A Tutorial on the Spectral Theory of Markov Chains. Neural Computation, 35 (11), 1713–1796. https://doi.org/10.1162/neco_a_01611
- Chen, X., Li, L., Shi, Q. (2015). Stochastic Evolutions of Dynamic Traffic Flow. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-44572-3
- Sadeghian, P., Han, M., Håkansson, J., Zhao, M. X. (2024). Testing feasibility of using a hidden Markov model on predicting human mobility based on GPS tracking data. Transportmetrica B: Transport Dynamics, 12 (1). https://doi.org/10.1080/21680566.2024.2336037
- Kravets, V. V., Kravets, Vl. V., Burov, О. V. (2016). Reliability of Systems. Part 2. Dynamics of Failures. Saarbrucken: Lap lambert Academic Publishing.
- Kravets, V. V., Bass, K. M., Kravets, V. V., Tokar, L. A. (2014). Analytical Solution of Kolmogorov Equations for Four-Condition Homogenous, Symmetric and Ergodic System. Open Journal of Applied Sciences, 04 (10), 497–500. https://doi.org/10.4236/ojapps.2014.410048
- Kravets, V., Kravets, V., Burov, O. (2021). Analytical Modeling of the Dynamic System of the Fourth Order. Transactions on Machine Learning and Artificial Intelligence, 9 (3), 14–24. https://doi.org/10.14738/tmlai.93.9947
- Domanskyi, I. V. (2016). Osnovy enerhoefektyvnosti elektrychnykh system z tiahovymy navantazhenniamy. Kharkiv: TOV «Tsentr informatsiyi transportu Ukrainy», 224. Available at: http://library.kpi.kharkov.ua/files/new_postupleniya/oceesi.pdf
- Kapitsa, M. I., Hryshechkina, T. S. (2014). Rational recovery model of depot processing equipment at the industrial enterprise. Science and Transport Progress, 4 (52), 60–66. https://doi.org/10.15802/stp2014/27319
- Yun, M., Qin, W., Yang, X., Liang, F. (2019). Estimation of urban route travel time distribution using Markov chains and pair-copula construction. Transportmetrica B: Transport Dynamics, 7 (1), 1521–1552. https://doi.org/10.1080/21680566.2019.1637798
- Suliankatchi Abdulkader, R., Deneshkumar, V., Senthamarai Kannan, K., Koyilil, V., Paes, A. T., Sebastian, T. (2021). An application of Markov chain modeling and semi-parametric regression for recurrent events in health data. Communications in Statistics: Case Studies, Data Analysis and Applications, 8 (1), 68–80. https://doi.org/10.1080/23737484.2021.1973926
- Ray, S. N., Bose, S., Chattopadhyay, S. (2020). A Markov chain approach to the predictability of surface temperature over the northeastern part of India. Theoretical and Applied Climatology, 143 (1-2), 861–868. https://doi.org/10.1007/s00704-020-03458-z
- Domanskyi, V., Domanskyi, I., Zakurdai, S., Liubarskyi, D. (2022). Development of technologies for selecting energy-efficient power supply circuits of railway traction networks. Technology Audit and Production Reserves, 4 (1 (66)), 47–54. https://doi.org/10.15587/2706-5448.2022.263961
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Victor Kravets, Mykhailo Kapitsa, Illia Domanskyi, Volodymyr Kravets, Tatiana Hryshechkina, Svitlana Zakurday

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.










