Determining optimal parameters of algebraic fractals in zero-knowledge authentication protocols
DOI:
https://doi.org/10.15587/1729-4061.2024.313471Keywords:
information security, network technologies, confidence, authentication, zero knowledge protocol, fractalAbstract
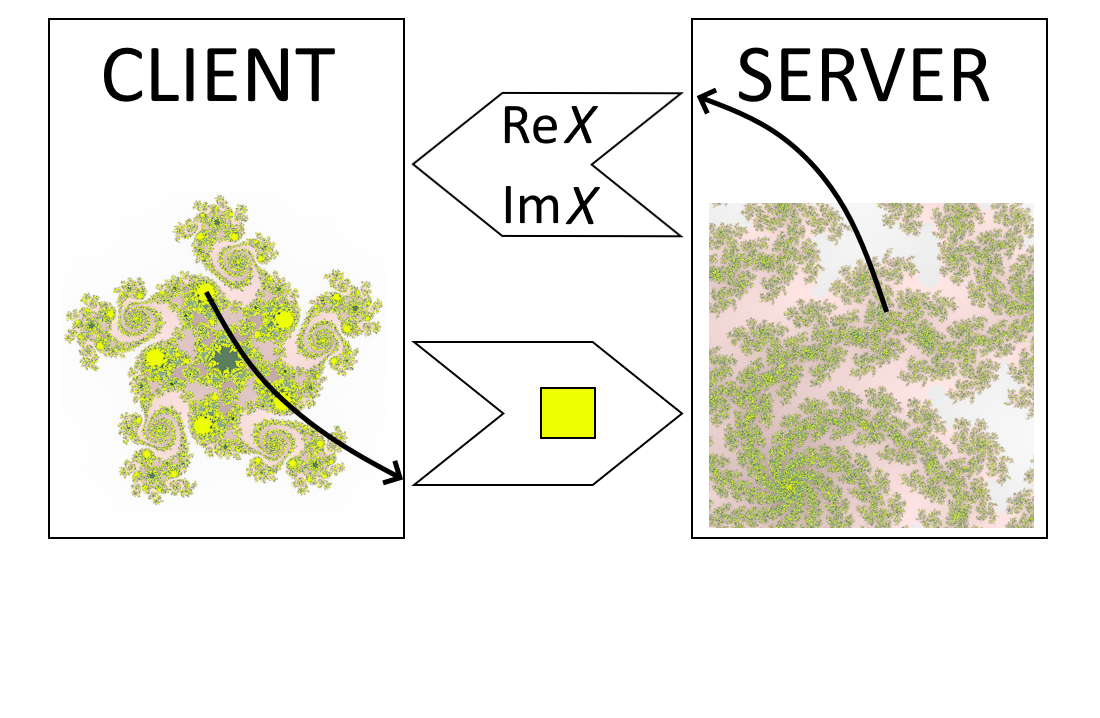
Most information systems, especially on the Internet, have a distributed architecture with remote access and an insecure communication channel. In such systems, the tasks of permanent authorization mean implementing time intervals of user work without re-authentication are especially actual. The problem is that repeatedly sending a password increases the likelihood of it corruption. One solution is to use zero-knowledge protocols. In these protocols, passwords are not transmitted over the channel but are included in the algorithms as parameters. However, the computational complexity, as well as the finite number of passwords, limit their use, ensuring the relevance of further research. Focusing on object of the exchange protocols security, the use of algebraic fractal sets has been proposed as a potentially infinite source of data for passwords. In this work, algorithms were developed, implemented, and tested, which proved the higher reliability of fractal protocols in comparison with the reference generator of random bits (with an error probability of 0.5). It was also noted that the calculation operations have an insignificant influence on the overall time complexity of the exchange protocol as a whole. Practical recommendations for the use of fractals with a Hausdorff dimensionally of about 1.6 on the boundary of the Mandelbrot set are given. The paper also highlights the advantages of including color information in fractal sets, which gives about 3 times improving of confidential security indicators of communication protocol. The proposed algorithms do not require specialized software and can be implemented in the majority of network information systems as an additional module.
References
- Nail, B., Atoussi, M. A., Saadi, S., Tibermacine, I. E., Napoli, C. (2024). Real-Time Synchronisation of Multiple Fractional-Order Chaotic Systems: An Application Study in Secure Communication. Fractal and Fractional, 8 (2), 104. https://doi.org/10.3390/fractalfract8020104
- Adeyemi, V.-A., Tlelo-Cuautle, E., Sandoval-Ibarra, Y., Nuñez-Perez, J.-C. (2023). FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission. Fractal and Fractional, 7 (6), 440. https://doi.org/10.3390/fractalfract7060440
- Jansen, B. H. (2000). Nonlinear methods for evoked potential analysis and modeling. Chaos in Brain?, 173–193. https://doi.org/10.1142/9789812793782_0014
- Bildirici, M. E., Ersin, Ö. Ö., Uçan, Y. (2024). Bitcoin, Fintech, Energy Consumption, and Environmental Pollution Nexus: Chaotic Dynamics with Threshold Effects in Tail Dependence, Contagion, and Causality. Fractal and Fractional, 8 (9), 540. https://doi.org/10.3390/fractalfract8090540
- Sulaiman, A. H., Baji, F. S. (2009). Fractal Based Fragile Watermark. 2009 Second International Conference on Computer and Electrical Engineering, 1, 139–143. https://doi.org/10.1109/iccee.2009.35
- Lock, A. J. J., Loh, C. H., Juhari, S. H., Samsudin, A. (2010). Compression-Encryption Based on Fractal Geometric. 2010 Second International Conference on Computer Research and Development, 3, 213–217. https://doi.org/10.1109/iccrd.2010.40
- Samoilenko, D. N. (2014). Authentication scheme on fractal sets. Ukrainian Information Security Research Journal, 16 (1). https://doi.org/10.18372/2410-7840.16.5396
- Schneier, B. (1996). Applied Cryptography. Protocols, Algorithms, and Source Code in C. John Wiley & Sons, 784. Available at: https://www.schneier.com/books/applied-cryptography/
- Giani, A. (2001). Identification with Zero Knowledge Protocols. SANS Institute. Available at: https://www.sans.org/reading-room/whitepapers/vpns/identification-zero-knowledge-protocols-719
- Gerardo, I. (2002). A Primer on Zero Knowledge Protocols. Universidad Nacional del Sur. Available at: http://cs.uns.edu.ar/~gis/publications/zkp-simari2002.pdf
- Feder, J. (1988). Fractals. Springer New York, 284. https://doi.org/10.1007/978-1-4899-2124-6
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Denys Samoilenko

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









