Визначення оптимальних параметрів алгебраїчних фракталів у протоколах автентифікації з нульовим розголошенням
DOI:
https://doi.org/10.15587/1729-4061.2024.313471Ключові слова:
інформаційна безпека, мережеві технології, конфіденційність, автентифікація, протокол без розголошення, фракталАнотація
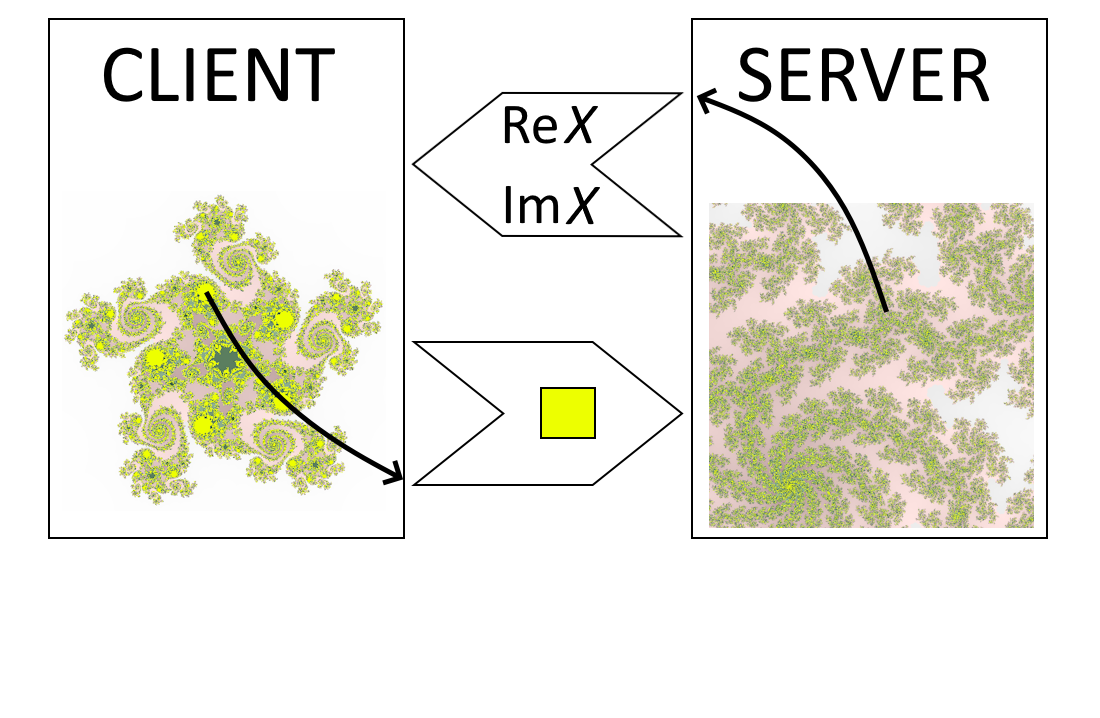
Більшість інформаційних систем, особливо в Інтернеті, мають розподілену архітектуру з віддаленим доступом та незахищеним каналом зв’язку. У таких системах особливо актуальні задачі перманентної авторизації, що реалізують часові проміжки роботи користувача без повторної автентифікації. Проблеми полягають у тому, що періодичне надсилання паролю збільшує імовірність його дискредитації. Одним зі способів рішення є використання протоколів з нульовим розголошенням. В цих протоколах паролі не передаються каналом, а входять до алгоритмів як параметри. Проте, обчислювальна складність, а також скінченна кількість паролів, обмежують їх використання, забезпечуючи актуальність подальших досліджень. Концентруючись на об’єкті безпеки обмінних протоколів було запропоновано використання алгебраїчних фрактальних множин як потенційно нескінченного джерела даних для паролів. У роботі обґрунтовані, реалізовані та випробувані алгоритми, які засвідчили більш високу надійність фрактальних протоколів у порівнянні з еталонним генератором випадкових біт (з імовірністю помилки 0,5). Також відзначено незначний вплив розрахункових операцій на загальну часову складність обмінного протоколу в цілому. Наведено практичні рекомендації щодо використання фракталів з хаусдорфівою розмірністю близько 1,6 на межі множини Мандельброта. Також у роботі показано переваги включення до фрактальних множин кольорової інформації, що дозволяє у 3 рази покращити такі показники безпеки як конфіденційність при обміні. Запропоновані алгоритми не вимагають спеціалізованого програмного забезпечення і можуть бути впроваджені у переважну більшість мережевих інформаційних систем у якості додаткового модуля
Посилання
- Nail, B., Atoussi, M. A., Saadi, S., Tibermacine, I. E., Napoli, C. (2024). Real-Time Synchronisation of Multiple Fractional-Order Chaotic Systems: An Application Study in Secure Communication. Fractal and Fractional, 8 (2), 104. https://doi.org/10.3390/fractalfract8020104
- Adeyemi, V.-A., Tlelo-Cuautle, E., Sandoval-Ibarra, Y., Nuñez-Perez, J.-C. (2023). FPGA Implementation of Parameter-Switching Scheme to Stabilize Chaos in Fractional Spherical Systems and Usage in Secure Image Transmission. Fractal and Fractional, 7 (6), 440. https://doi.org/10.3390/fractalfract7060440
- Jansen, B. H. (2000). Nonlinear methods for evoked potential analysis and modeling. Chaos in Brain?, 173–193. https://doi.org/10.1142/9789812793782_0014
- Bildirici, M. E., Ersin, Ö. Ö., Uçan, Y. (2024). Bitcoin, Fintech, Energy Consumption, and Environmental Pollution Nexus: Chaotic Dynamics with Threshold Effects in Tail Dependence, Contagion, and Causality. Fractal and Fractional, 8 (9), 540. https://doi.org/10.3390/fractalfract8090540
- Sulaiman, A. H., Baji, F. S. (2009). Fractal Based Fragile Watermark. 2009 Second International Conference on Computer and Electrical Engineering, 1, 139–143. https://doi.org/10.1109/iccee.2009.35
- Lock, A. J. J., Loh, C. H., Juhari, S. H., Samsudin, A. (2010). Compression-Encryption Based on Fractal Geometric. 2010 Second International Conference on Computer Research and Development, 3, 213–217. https://doi.org/10.1109/iccrd.2010.40
- Samoilenko, D. N. (2014). Authentication scheme on fractal sets. Ukrainian Information Security Research Journal, 16 (1). https://doi.org/10.18372/2410-7840.16.5396
- Schneier, B. (1996). Applied Cryptography. Protocols, Algorithms, and Source Code in C. John Wiley & Sons, 784. Available at: https://www.schneier.com/books/applied-cryptography/
- Giani, A. (2001). Identification with Zero Knowledge Protocols. SANS Institute. Available at: https://www.sans.org/reading-room/whitepapers/vpns/identification-zero-knowledge-protocols-719
- Gerardo, I. (2002). A Primer on Zero Knowledge Protocols. Universidad Nacional del Sur. Available at: http://cs.uns.edu.ar/~gis/publications/zkp-simari2002.pdf
- Feder, J. (1988). Fractals. Springer New York, 284. https://doi.org/10.1007/978-1-4899-2124-6
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Denys Samoilenko

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









