Developing of neural network computing methods for solving inverse elasticity problems

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.313795

Keywords:

physics-informed neural networks, inverse problems, geometric nonlinearity

Abstract

This paper examines the use of neural network methods to solve inverse problems in the mechanics of elastic materials.

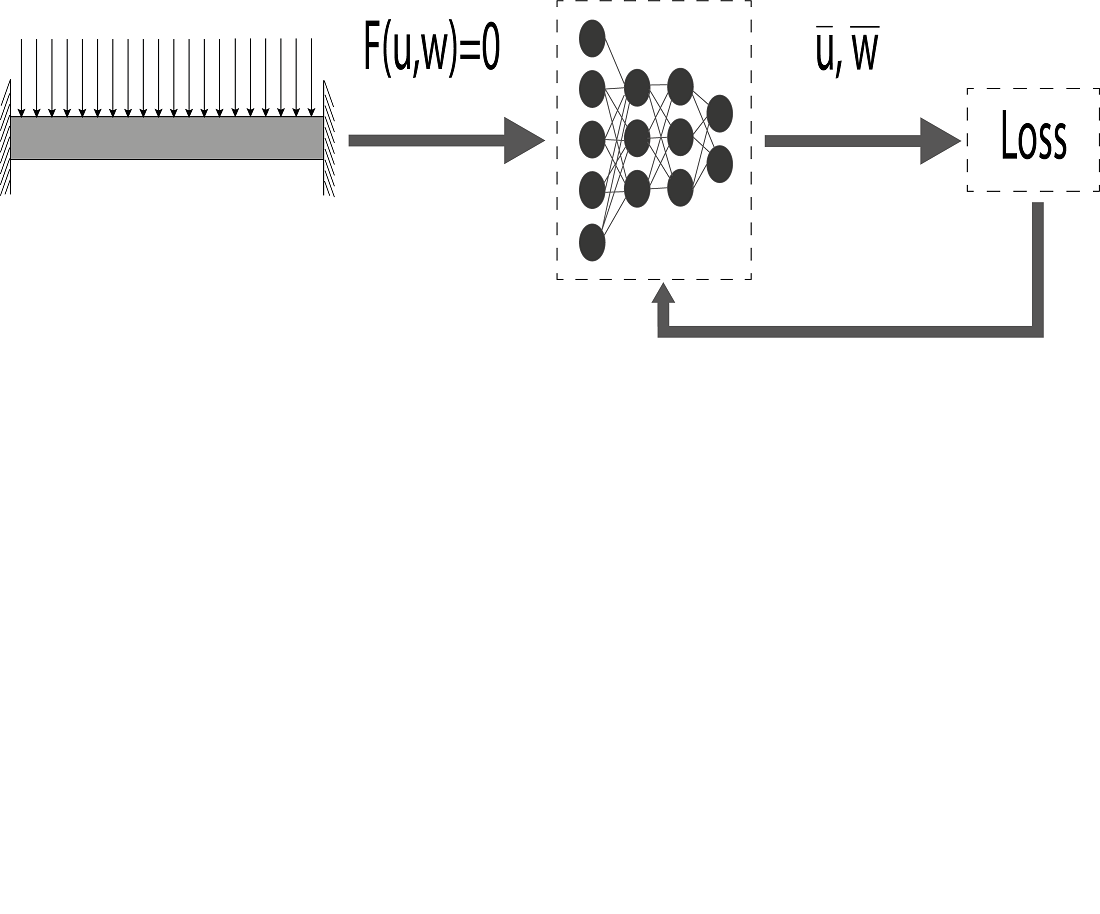
The aim is to design physics-informed neural networks that can predict the parameters of structural components, and the physical properties of materials based on a specified displacement distribution.

A key feature of the specified neural networks is the integration of differential equations and boundary conditions into the loss function calculation. This approach ensures that the error in approximating unknown functions has a direct impact on optimizing the network's weights. As a result, the resulting neural network approximations of unknown functions comply with the differential equations and boundary conditions.

To test the capabilities of the designed neural networks, inverse problems involving the bending of plates and beams have been solved, focusing on determining one or two unknown parameters. Comparison of predicted and exact values demonstrates high accuracy of the constructed neural network models, with a relative prediction error of less than 3 % across all cases.

Unlike analytical methods for solving inverse problems, the primary advantage of physics-informed neural networks is their flexibility when addressing both linear and nonlinear problems. For instance, the same network architecture can be employed to solve various boundary-value problems without modification. Compared to classical numerical methods, the parallelization capability of neural networks is inherently supported by modern software libraries.

Therefore, the application of physics-informed neural networks for solving inverse elasticity problems of plates and beams is effective, as evidenced by the achieved relative errors and the computational robustness of the method. In practice, the proposed solution can be used for relevant calculations during the design of structural elements. The developed software code can also be integrated into automated design systems or computer algebra systems

Author Biographies

Anastasiia Kaliuzhniak, Zaporizhzhia National University

PhD

Department of Computer Science

Oleksii Kudin, Zaporizhzhia National University

PhD, Associate Professor

Department of Software Engineering

Yuriy Belokon, Zaporizhzhia National University

Doctorof Technical Sciences, Professor

Department of Metallurgical Technologies, Ecology and Technological Safety

Dmytro Kruglyak, Zaporizhzhia National University

PhD, Associate Professor

Department of Metallurgical Technologies, Ecology and Technological Safety

References

  1. Edwards, C. H., Penney, D. E., Calvis, D. T. (2014). Differential Equations and Boundary Value Problems: Computing and Modeling. Boston: Pearson, 797.
  2. Pinder, G. F. (2018). Numerical Methods for Solving Partial Differential Equations. Wiley, 304.
  3. Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., Yang, L. (2021). Physics-informed machine learning. Nature Reviews Physics, 3 (6), 422–440. https://doi.org/10.1038/s42254-021-00314-5
  4. Willard, J., Jia, X., Xu, S., Steinbach, M., Kumar, V. (2022). Integrating Scientific Knowledge with Machine Learning for Engineering and Environmental Systems. ACM Computing Surveys, 55 (4), 1–37. https://doi.org/10.1145/3514228
  5. Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals, and Systems, 2 (4), 303–314. https://doi.org/10.1007/bf02551274
  6. Lagaris, I. E., Likas, A., Fotiadis, D. I. (1998). Artificial neural networks for solving ordinary and partial differential equations. IEEE Transactions on Neural Networks, 9 (5), 987–1000. https://doi.org/10.1109/72.712178
  7. Raissi, M., Perdikaris, P., Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707. https://doi.org/10.1016/j.jcp.2018.10.045
  8. Yarosh, A. O., Kudin, O. V. (2024). Neural network methods for solving elasticity problems. Visnyk of Kherson National Technical University, 1 (88), 295–305. https://doi.org/10.35546/kntu2078-4481.2024.1.41
  9. Meethal, R. E., Kodakkal, A., Khalil, M., Ghantasala, A., Obst, B., Bletzinger, K.-U., Wüchner, R. (2023). Finite element method-enhanced neural network for forward and inverse problems. Advanced Modeling and Simulation in Engineering Sciences, 10 (1). https://doi.org/10.1186/s40323-023-00243-1
  10. Lu, L., Meng, X., Mao, Z., Karniadakis, G. E. (2021). DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Review, 63 (1), 208–228. https://doi.org/10.1137/19m1274067
  11. Zhou, H., Pu, J., Chen, Y. (2023). Data-driven forward–inverse problems for the variable coefficients Hirota equation using deep learning method. Nonlinear Dynamics, 111 (16), 14667–14693. https://doi.org/10.1007/s11071-023-08641-1
  12. Zhong, M., Yan, Z. (2023). Data-driven forward and inverse problems for chaotic and hyperchaotic dynamic systems based on two machine learning architectures. Physica D: Nonlinear Phenomena, 446, 133656. https://doi.org/10.1016/j.physd.2023.133656
  13. Depina, I., Jain, S., Mar Valsson, S., Gotovac, H. (2021). Application of physics-informed neural networks to inverse problems in unsaturated groundwater flow. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 16 (1), 21–36. https://doi.org/10.1080/17499518.2021.1971251
  14. Garay, J., Dunstan, J., Uribe, S., Costabal, F. S. (2023). Physics-informed neural networks for blood flow inverse problems. arXiv. https://doi.org/10.48550/arXiv.2308.00927
  15. Mao, Z., Jagtap, A. D., Karniadakis, G. E. (2020). Physics-informed neural networks for high-speed flows. Computer Methods in Applied Mechanics and Engineering, 360, 112789. https://doi.org/10.1016/j.cma.2019.112789
  16. Wang, Z. Q., Jiang, J., Tang, B. T., Zheng, W. (2014). High Precision Numerical Analysis of Nonlinear Beam Bending Problems under Large Deflection. Applied Mechanics and Materials, 638-640, 1705–1709. https://doi.org/10.4028/www.scientific.net/amm.638-640.1705
  17. Wu, C., Zhu, M., Tan, Q., Kartha, Y., Lu, L. (2023). A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 403, 115671. https://doi.org/10.1016/j.cma.2022.115671
  18. AutoPINN. Available at: https://github.com/avk256/AutoPINN
  19. Segall, A. E. (2023). The Search for a Generalized Analytical Solution for the Inverse Problem; Some Surprisingly Simple Approximate Methods for Problems of Practical Importance. Journal of Physics: Conference Series, 2444 (1), 012013. https://doi.org/10.1088/1742-6596/2444/1/012013
  20. Kern, M. (2016). Numerical Methods for Inverse Problems. Wiley. https://doi.org/10.1002/9781119136941
Developing of neural network computing methods for solving inverse elasticity problems

Downloads

Published

2024-12-20

How to Cite

Kaliuzhniak, A., Kudin, O., Belokon, Y., & Kruglyak, D. (2024). Developing of neural network computing methods for solving inverse elasticity problems. Eastern-European Journal of Enterprise Technologies, 6(7 (132), 45–52. https://doi.org/10.15587/1729-4061.2024.313795

Issue

Vol. 6 No. 7 (132) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2024 Anastasiia Kaliuzhniak, Oleksii Kudi, Yuriy Belokon, Dmytro Kruglyak

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.