Generation, evaluation and comparison of DNA-based (pseudo) random sequences

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.314808

Keywords:

DNA, random sequences, randomness extractors, statistical testing, similarity evaluation, k-mers, MinHash

Abstract

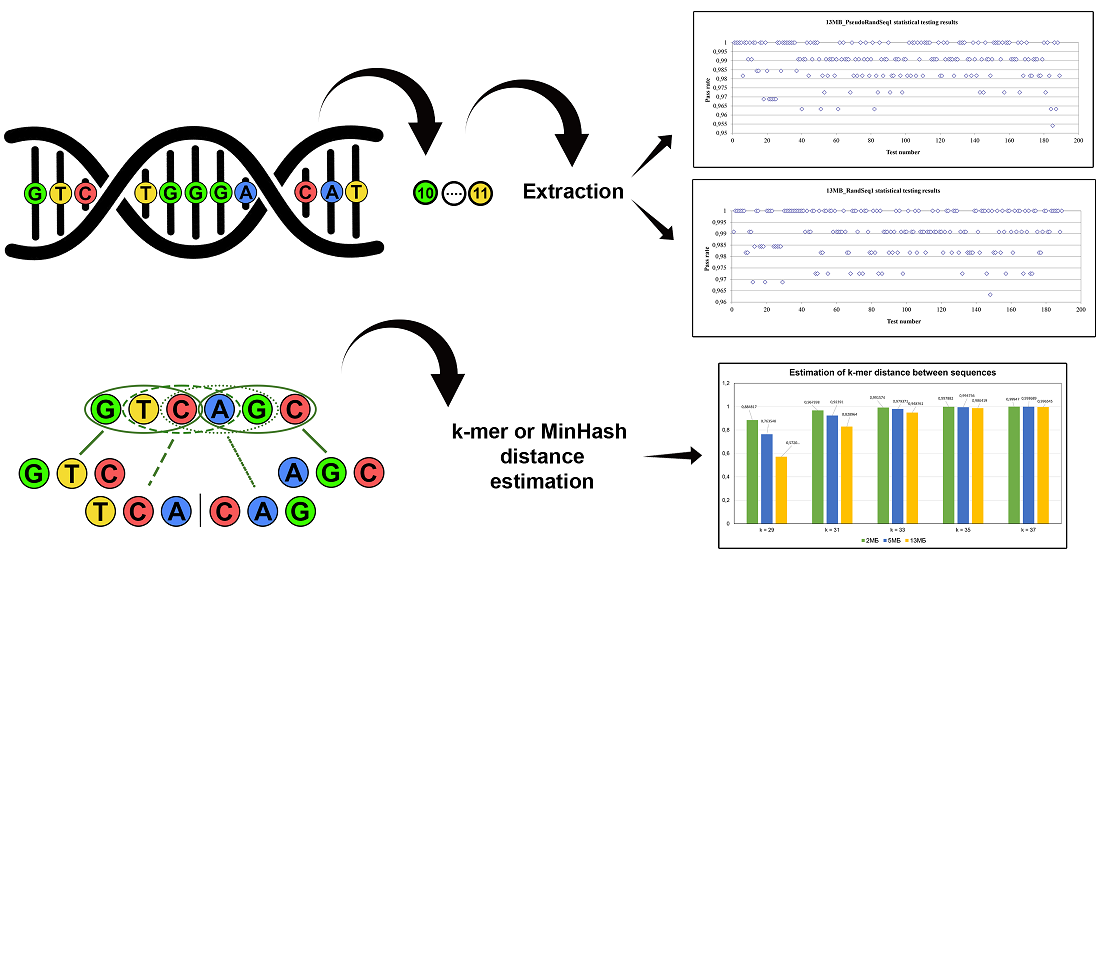
The object of this study is the methods and algorithms for computing, evaluating, and comparing DNA-based pseudorandom sequences (PRSs) and random sequences (RSs). This paper addresses the task of extracting (P)RSs with the required stochastic and statistical properties from a DNA noise source, experimentally validating these properties in compliance with the requirements of current international standards, as well as evaluating and comparing the sequences obtained for different DNA samples. The results are the developed algorithms for generating DNA-based (P)RSs, improved algorithms for their comparison, and proposals for the process of evaluating their properties. For the output of implemented algorithms, more than 96 % of the bit streams of sequences successfully pass all statistical tests, and the entropy per bit for RSs is close to 1. A special feature of the developed generation algorithms is the use of validated conditioning component – block cipher in CTR mode – which explains the possibility of obtaining unique random data with required properties. The peculiarity of the proposed evaluation algorithm is the complexity of the tests and checks used: complete assessment of statistical properties and entropy values. Special features of the improved comparison algorithms are resource saving and the ability to evaluate much larger data sets. This is due to the use of structures and data types that are better in terms of memory usage and flexible cryptographic primitives with different modes.

The results could be practically applied to constructs where randomness is required: for computing the keys and system-wide parameters, when performing transformations as part of hash functions, while obtaining sequences of an arbitrary alphabet, in zero-knowledge protocols, etc.

Author Biographies

Ivan Gorbenko, V. N. Karazin Kharkiv National University; JSC “Institute of Information Technologies”

Doctor of Technical Sciences, Professor

Department of Cybersecurity of Information Systems, Networks and Technologies

Yaroslav Derevianko, V. N. Karazin Kharkiv National University; JSC “Institute of Information Technologies”

PhD Student

Department of Cybersecurity of Information Systems, Networks and Technologies

References

  1. Goldreich, O. (2001). Foundations of Cryptography. Cambridge University Press. https://doi.org/10.1017/cbo9780511546891
  2. Matthias, P., Werner, S. (2023). A Proposal for Functionality Classes for Random Number Generators. Version 2.36 – Current intermediate document for the AIS 20/31 workshop. Available at: https://www.bsi.bund.de/SharedDocs/Downloads/EN/BSI/Certification/Interpretations/AIS_31_Functionality_classes_for_random_number_generators_e_2023.pdf?__blob=publicationFile&v=2
  3. Horbenko, I., Derevianko, Ya., Horbenko, D. (2024). DNK – dzherelo shumu ta nefizychnykh vypadkovykh poslidovnostei. Osnovni polozhennia praktychnykh doslidzhen. II Mizhnarodna naukovo-praktychna konferentsiya «Kiberborotba: rozvidka, zakhyst ta protydiya», 30–31. Available at: https://cyberwarfare.viti.edu.ua/assets/files/Cyberwarfare_2024.pdf
  4. Turan, M. S., Barker, E., Kelsey, J., McKay, K., Baish, M., Boyle, M. (2018). NIST SP 800-90B. Recommendation for the Entropy Sources Used for Random Bit Generation. NIST. https://doi.org/10.6028/NIST.SP.800-90B
  5. Rukhin, A., Soto, J., Nechvatal, J., Smid, M., Barker, E., Leigh, S. et al. (2010). NIST Special Publication 800-22 Revision 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Available at: https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-22r1a.pdf
  6. Extractors and Pseudorandom Generators (2001). Journal of the ACM (JACM), 48 (4), 860–879. https://doi.org/10.1145/502090.502099
  7. Barman, P., Djilali, B., Benatmane, S., Nuh, A. (2024). A New Hybrid Cryptosystem Involving DNA, Rabin, One Time Pad and Fiestel. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.4771411
  8. Zhang, Y., Liu, X., Sun, M. (2017). DNA based random key generation and management for OTP encryption. Biosystems, 159, 51–63. https://doi.org/10.1016/j.biosystems.2017.07.002
  9. Siddaramappa, V., Ramesh, K. B. (2020). True Random Number Generation Based on DNA molecule Genetic Information (DNA-TRNG). Cryptology ePrint Archive, Paper 2020/745. Available at: https://eprint.iacr.org/2020/745.pdf
  10. Li, Z., Peng, C., Tan, W., Li, L. (2020). A Novel Chaos-Based Image Encryption Scheme by Using Randomly DNA Encode and Plaintext Related Permutation. Applied Sciences, 10 (21), 7469. https://doi.org/10.3390/app10217469
  11. Sievers, F., Higgins, D. G. (2017). Clustal Omega for making accurate alignments of many protein sequences. Protein Science, 27 (1), 135–145. https://doi.org/10.1002/pro.3290
  12. Tu, S.-L., Staheli, J. P., McClay, C., McLeod, K., Rose, T. M., Upton, C. (2018). Base-By-Base Version 3: New Comparative Tools for Large Virus Genomes. Viruses, 10 (11), 637. https://doi.org/10.3390/v10110637
  13. Beretta, S. (2019). Algorithms for Strings and Sequences: Pairwise Alignment. Encyclopedia of Bioinformatics and Computational Biology, 22–29. https://doi.org/10.1016/b978-0-12-809633-8.20317-8
  14. Needleman, S. B., Wunsch, C. D. (1970). A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology, 48 (3), 443–453. https://doi.org/10.1016/0022-2836(70)90057-4
  15. Shanker, K. P. S., Austin, J., Sherly, E. (2010). An Algorithm for alignment-free sequence comparison using Logical Match. 2010 The 2nd International Conference on Computer and Automation Engineering (ICCAE), 536–538. https://doi.org/10.1109/iccae.2010.5452072
  16. Wilkinson, S. (2022). Fast K-Mer Counting and Clustering for Biological Sequence Analysis. Available at: https://cran.r-project.org/web/packages/kmer/kmer.pdf
  17. Ondov, B. D., Treangen, T. J., Melsted, P., Mallonee, A. B., Bergman, N. H., Koren, S., Phillippy, A. M. (2016). Mash: fast genome and metagenome distance estimation using MinHash. Genome Biology, 17 (1). https://doi.org/10.1186/s13059-016-0997-x
  18. Broder, A. Z. (1997). On the resemblance and containment of documents. Proceedings. Compression and Complexity of SEQUENCES 1997 (Cat. No.97TB100171). https://doi.org/10.1109/sequen.1997.666900
  19. Barker, E., Kelsey, J. (2015). NIST SP 800-90A Rev. 1. Recommendation for Random Number Generation Using Deterministic Random Bit Generators. NIST. http://dx.doi.org/10.6028/NIST.SP.800-90Ar1
  20. Holubnychiy, D. Yu., Kandiy, S. O., Yesina, M. V., Gorbenko, D. Yu. (2024). Methods and means for analysing, evaluating and comparing properties of random sequences and random numbers. Radiotekhnika, 1 (216), 30–45. https://doi.org/10.30837/rt.2024.1.216.02
  21. Müller, S. (2024). Linux /dev/random – A New Approach. Available at: https://www.chronox.de/lrng/releases/v53/lrng-v53.pdf
  22. Index of /genbank. Available at: https://ftp.ncbi.nlm.nih.gov/genbank/
  23. DNA Data Bank of Japan. Available at: https://www.ddbj.nig.ac.jp/index-e.html
  24. Contreras Rodríguez, L., Madarro-Capó , E. J., Legón-Pérez , C. M., Rojas, O., Sosa-Gómez, G. (2021). Selecting an Effective Entropy Estimator for Short Sequences of Bits and Bytes with Maximum Entropy. Entropy, 23 (5), 561. https://doi.org/10.3390/e23050561
  25. Skorski, M. (2016). Improved Estimation of Collision Entropy in High and Low-Entropy Regimes and Applications to Anomaly Detection. Cryptology ePrint Archive, Paper 2016/1035. Available at: https://eprint.iacr.org/2016/1035
  26. Quantis QRNG USB. Available at: https://www.idquantique.com/random-number-generation/products/quantis-random-number-generator/
  27. Aparatnyi HVCh «Hriada-3». AT «IIT». Available at: https://iit.com.ua/index.php?page=itemdetails&p=3&gtype=1&type=1&id=96
  28. Chi-Square Goodness-of-Fit Test. NIST Engineering Statistics Handbook. Available at: https://www.itl.nist.gov/div898/handbook/eda/section3/eda35f.htm
  29. Genome Assembly Workshop 2020. UCDavis Bioinformatics Core. Available at: https://ucdavis-bioinformatics-training.github.io/2020-Genome_Assembly_Workshop/kmers/kmers
  30. Edgar, R. C. (2004). Local homology recognition and distance measures in linear time using compressed amino acid alphabets. Nucleic Acids Research, 32 (1), 380–385. https://doi.org/10.1093/nar/gkh180
  31. Kelsey, J. (2005). SHA-160: A Truncation Mode for SHA256 (and most other hashes). NIST. Available at: https://csrc.nist.gov/csrc/media/events/first-cryptographic-hash-workshop/documents/kelsey_truncation.pdf
  32. Dang, Q. (2009). NIST Special Publication 800-107. Recommendation for Applications Using Approved Hash Algorithms. NIST. Available at: https://csrc.nist.rip/library/NIST%20SP%20800-107%20Recommendation%20for%20Apps%20Using%20Approved%20Hash%20Algorithms,%202009-02.pdf
  33. Gorbenko, I. D., Alekseychuk, A. N., Kachko, Ye. G., Derevianko, Ya. A. (2024). Research into methods and algorithms for generating (pseudo) random sequences over an arbitrary alphabet. Radiotekhnika, 216, 7–29. https://doi.org/10.30837/rt.2024.1.216.01
Generation, evaluation and comparison of DNA-based (pseudo) random sequences

Downloads

Published

2024-11-12

How to Cite

Gorbenko, I., & Derevianko, Y. (2024). Generation, evaluation and comparison of DNA-based (pseudo) random sequences. Eastern-European Journal of Enterprise Technologies, 6(9 (132), 6–24. https://doi.org/10.15587/1729-4061.2024.314808

Issue

Vol. 6 No. 9 (132) (2024): Information and controlling system

Section

Information and controlling system

License

Copyright (c) 2024 Ivan Gorbenko, Yaroslav Derevianko

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.