Determining the deformation of an absolutely elastic axis of curved rods under bending
DOI:
https://doi.org/10.15587/1729-4061.2024.317338Keywords:
arc length, concentrated force, pulsating loads, axis curvature, cantilever fasteningAbstract
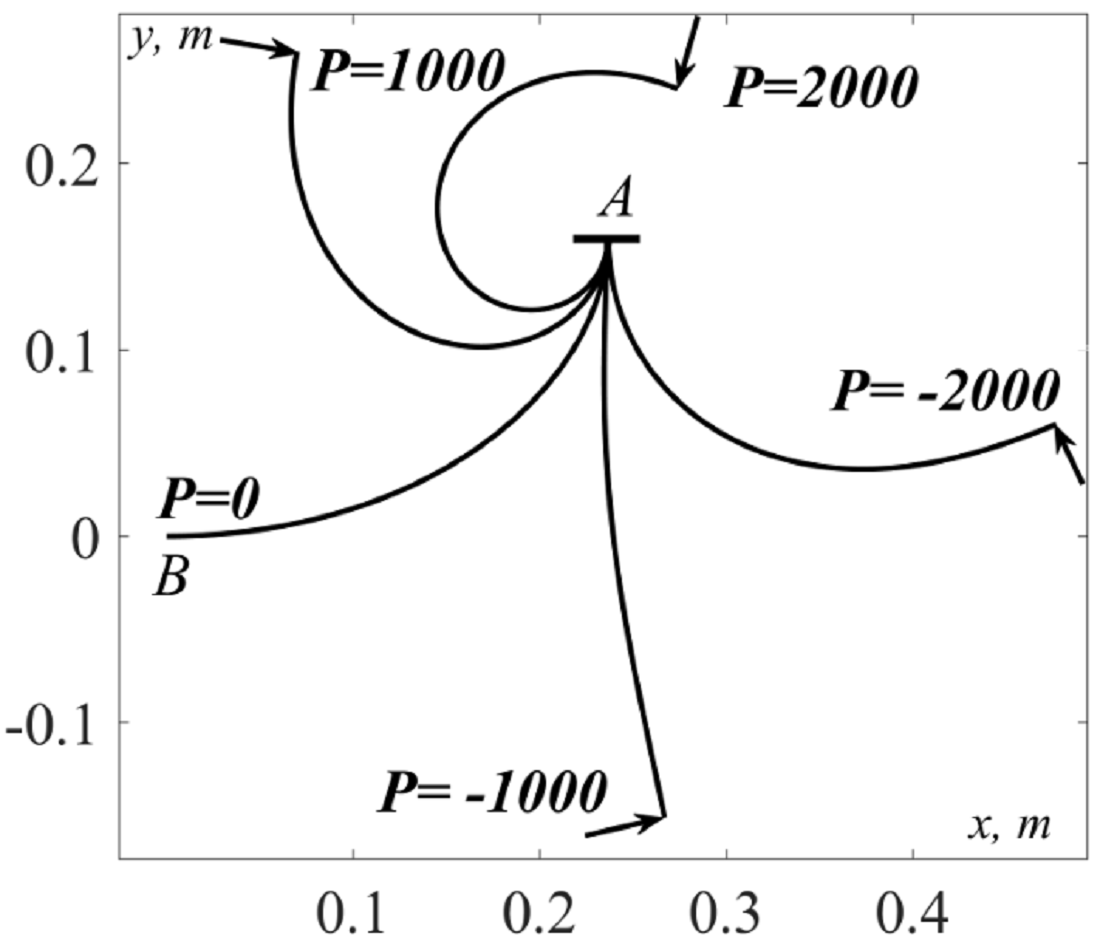
The object of this study is the deformation of an elastic axis with a large deflection of a cantilever clamped absolutely elastic rod under the action of an applied concentrated force. The rod in the free state can have a rectilinear or curved elastic axis. This fact implies a difference in the analytical description of the bending process. However, there is a factor by which some similarity can be found between the bending of rectilinear and curved rods. This factor is the curvature of the elastic axis of the rod in a free state. According to this feature, they can be divided into rods of constant and variable curvature of the elastic axis. The former include rectilinear rods and those that in the free state have the shape of an arc of a circle, and the latter – rods with a variable curvature of the elastic axis. There is a difference between the bending of these groups of rods: in the first case, the deformation of the elastic axis of the rod during its bending will be the same regardless of which end will be cantilever pinched.
A distinctive feature of the current research is that the bending of rods with variable curvature of the elastic axis was carried out by alternate pinching of their opposite ends. Moreover, the rods of constant and variable curvature were of the same length s=0.314 m, the same cross-section of 0.005×0.02 m. That has made it possible to visually show the difference between the shape of the elastic axis of the bent rod under the action of the same force when the pinch end is changed. When attached to the rods of the working bodies of agricultural machines, pulsating dynamic loads are smoothed out due to their elasticity. It is important for practice to be able to calculate the value of their deviation, which should be within the given limits.
The results are explained by the fact that in the analytical description of the shape of the elastic axis of a curved rod, a technique was proposed in which the length of the axis can start counting both from one end and from the opposite end
References
- Kobets, A., Aliiev, E., Tesliuk, H., Aliieva, O. (2023). Simulation of the process of interaction of the working bodies of tillage machines with the soil in Simcenter STAR-CCM+. Naukovij Žurnal «Tehnìka Ta Energetika», 14 (1). https://doi.org/10.31548/machinery/1.2023.09
- Budzanivskyi, M. (2022). Mathematical modelling of oscillations of a machine for cutting tops of root crops. Naukovij Žurnal «Tehnìka Ta Energetika», 13 (4). https://doi.org/10.31548/machenergy.13(4).2022.16-27
- Kozachenko, O. V., Syedykh, K. V. (2020). Dynamic model of process of deformation of elastic rack of disk cultivator. Naukovij žurnal «Tehnìka ta energetika», 11 (3), 31–39. https://doi.org/10.31548/machenergy2020.03.031
- Sereda, L., Kovalchuk, D. (2021). Mathematical modeling soil tilling unit in the system "soil-aggregate-energy means" for Strip-Till technology soil treatment. Naukovij žurnal «Tehnìka ta energetika», 12 (4), 103–108. https://doi.org/10.31548/machenergy2021.04.103
- Zhang, X., Hu, J., Chen, S. (2023). Study on Stability of Elastic Compression Bending Bar in Viscoelastic Medium. Applied Sciences, 13 (19), 11111. https://doi.org/10.3390/app131911111
- Pylypaka, S., Volina, T., Hropost, V., Babka, V., Hryshchenko, I. (2023). Determination of the form of a spiral spring in a free state. ScienceRise, 3, 3–9. https://doi.org/10.21303/2313-8416.2023.003213
- Pagani, A., Carrera, E. (2017). Large-deflection and post-buckling analyses of laminated composite beams by Carrera Unified Formulation. Composite Structures, 170, 40–52. https://doi.org/10.1016/j.compstruct.2017.03.008
- Ghuku, S., Saha, K. (2020). Large Deflection of Clamped Curved Beam Under Finite Clamping and Different Combinations of Bending-Stretching. Engineering Science & Technology, 121–134. https://doi.org/10.37256/est.212021548
- Wu, K., Zheng, G. (2022). Insight into numerical solutions of static large deflection of general planar beams for Compliant Mechanisms. Mechanism and Machine Theory, 172, 104757. https://doi.org/10.1016/j.mechmachtheory.2022.104757
- Wu, K., Zheng, G. (2021). Theoretical Analysis on Nonlinear Buckling, Post-Buckling of Slender Beams and Bi-Stable Mechanisms. Journal of Mechanisms and Robotics, 14 (3). https://doi.org/10.1115/1.4053047
- Eroglu, U. (2016). Large deflection analysis of planar curved beams made of Functionally Graded Materials using Variational Iterational Method. Composite Structures, 136, 204–216. https://doi.org/10.1016/j.compstruct.2015.10.017
- Nadykto, V. T., Tikhovod, M. A. (2020). Harrow section movement sustainability analysis. Naukovij Žurnal «Tehnìka Ta Energetika», 11 (2), 95–105. https://doi.org/10.31548/machenergy2020.02.095
- Gaponova, O., Kundera, Cz., Kirik, G., Tarelnyk, V., Martsynkovskyy, V., Konoplianchenko, Ie. et al. (2019). Estimating Qualitative Parameters of Aluminized Coating Obtained by Electric Spark Alloying Method. Advances in Thin Films, Nanostructured Materials, and Coatings, 249–266. https://doi.org/10.1007/978-981-13-6133-3_25
- Tarelnyk, V. B., Gaponova, O. P., Loboda, V. B., Konoplyanchenko, E. V., Martsinkovskii, V. S., Semirnenko, Yu. I. et al. (2021). Improving Ecological Safety when Forming Wear-Resistant Coatings on the Surfaces of Rotation Body Parts of 12Kh18N10T Steel Using a Combined Technology Based on Electrospark Alloying. Surface Engineering and Applied Electrochemistry, 57 (2), 173–184. https://doi.org/10.3103/s1068375521020113
- Wadi, K. J., Yadeem, J. M., Mustafa khazaal, S., Al-Ansari, L. S., Abdulsamad, H. J. (2022). Static deflection calculation for axially FG cantilever beam under uniformly distributed and transverse tip loads. Results in Engineering, 14, 100395. https://doi.org/10.1016/j.rineng.2022.100395
- Diwan, A. A., Al-Ansari, L. S., Al-Saffar, A. A., Al-Anssari, Q. S. (2019). Experimental and theoretical investigation of static deflection and natural frequency of stepped cantilever beam. Australian Journal of Mechanical Engineering, 20 (2), 303–315. https://doi.org/10.1080/14484846.2019.1704494
- Alansari, L. S., Abdulsamad, H. J., Wadi, K. J., Al-Raheem, S. Kh. (2021). Investigation of static deflection in internal stepped cantilever beam. Journal of Mechanical Engineering Research and Developments, 44 (5), 87–125.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Serhii Pylypaka, Victor Nesvidomin, Tetiana Volina, Iryna Hryshchenko, Taras Pylypaka, Yaroslav Kremets, Serhii Andrukh, Oleksandr Savoiskyi, Larysa Korzh-Usenko, Yuriy Semirnenko

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









