Визначення деформації абсолютно пружної осі криволінійних стержнів при їх згинанні
DOI:
https://doi.org/10.15587/1729-4061.2024.317338Ключові слова:
довжина дуги, зосереджена сила, пульсуючі навантаження, кривина осі, консольне закріпленняАнотація
Об’єктом дослідження є деформація пружної осі з великим прогином консольно защемленого абсолютно пружного стержня під дією прикладеної зосередженої сили. Стержень у вільному стані може мати прямолінійну або криволінійну пружну вісь. Цей факт передбачає відмінність у аналітичному описі процесу згинання. Однак існує фактор, за яким можна знайти певну подібність між згинанням прямолінійних і криволінійних стержнів. Цим фактором є кривина пружної осі стержня у вільному стані. За цією ознакою їх можна розділити на стержні сталої і змінної кривини пружної осі. До перших відносяться прямолінійні стержні і ті, які у вільному стані мають форму дуги кола, до других – стержні із змінною кривиною пружної осі. Між згинанням цих груп стержнів існує відмінність: в першому випадку деформація пружної осі стержня при його згинанні буде однаковою незалежно від того, який кінець буде консольно защемлений.
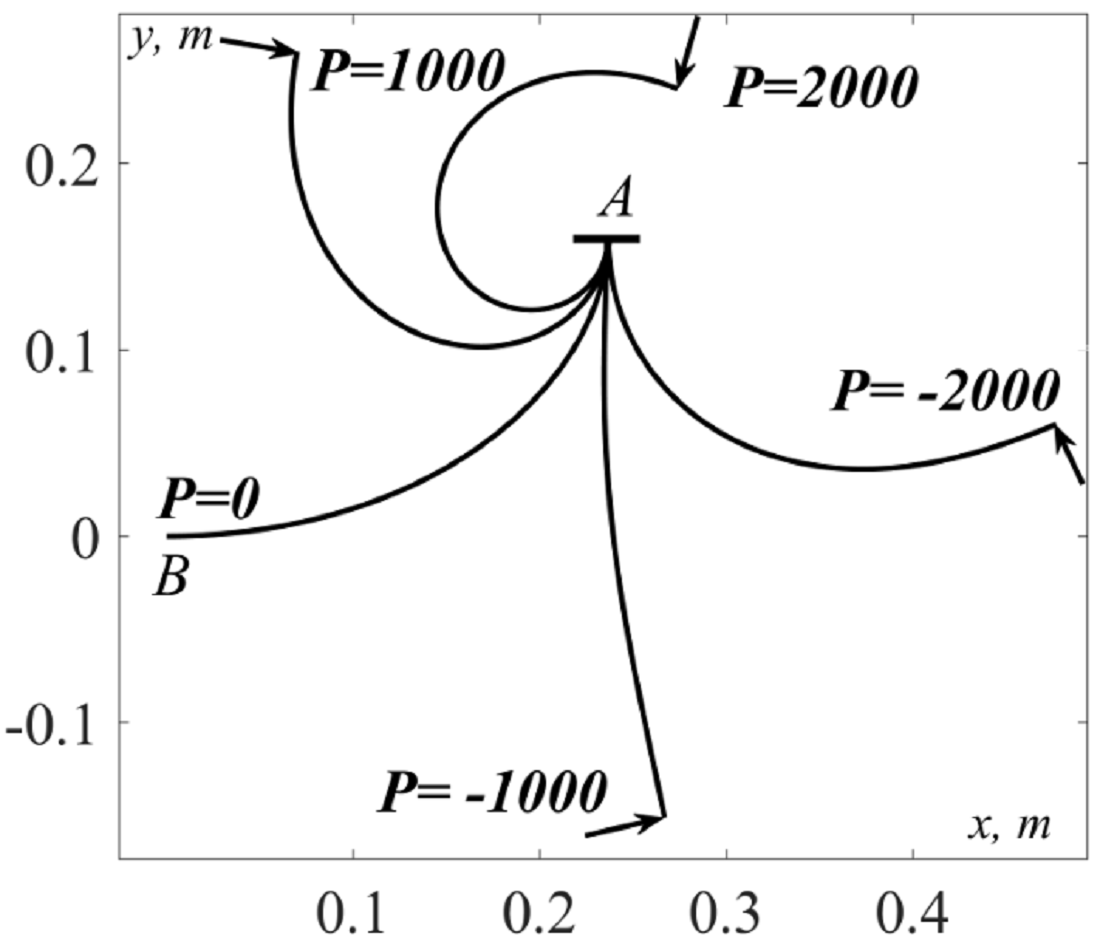
Відмінною особливістю даного дослідження від існуючих є те, що згинання стержнів із змінною кривиною пружної осі проводилося при почерговому защемленні їх протилежних кінців. Причому стержні сталої і змінної кривини були однакової довжини s=0,314 м, однакового поперечного перерізу 0,005×0,02 м. Це дозволило наочно показати відмінність між формою пружної осі зігнутого стержня під дією однієї ж і тієї сили при зміні кінця защемлення. При кріпленні до стержнів робочих органів сільськогосподарських машин завдяки їх пружності згладжуються пульсуючі динамічні навантаження. Важливою для практики є можливість розрахунку величини їх відхилення, яка повинна бути в заданих межах.
Отримані результати пояснюються тим, що при аналітичному описі форми пружної осі криволінійного стержня було запропоновано спосіб, при якому довжина осі може починати відлік як від одного, так і від протилежного кінця
Посилання
- Kobets, A., Aliiev, E., Tesliuk, H., Aliieva, O. (2023). Simulation of the process of interaction of the working bodies of tillage machines with the soil in Simcenter STAR-CCM+. Naukovij Žurnal «Tehnìka Ta Energetika», 14 (1). https://doi.org/10.31548/machinery/1.2023.09
- Budzanivskyi, M. (2022). Mathematical modelling of oscillations of a machine for cutting tops of root crops. Naukovij Žurnal «Tehnìka Ta Energetika», 13 (4). https://doi.org/10.31548/machenergy.13(4).2022.16-27
- Kozachenko, O. V., Syedykh, K. V. (2020). Dynamic model of process of deformation of elastic rack of disk cultivator. Naukovij žurnal «Tehnìka ta energetika», 11 (3), 31–39. https://doi.org/10.31548/machenergy2020.03.031
- Sereda, L., Kovalchuk, D. (2021). Mathematical modeling soil tilling unit in the system "soil-aggregate-energy means" for Strip-Till technology soil treatment. Naukovij žurnal «Tehnìka ta energetika», 12 (4), 103–108. https://doi.org/10.31548/machenergy2021.04.103
- Zhang, X., Hu, J., Chen, S. (2023). Study on Stability of Elastic Compression Bending Bar in Viscoelastic Medium. Applied Sciences, 13 (19), 11111. https://doi.org/10.3390/app131911111
- Pylypaka, S., Volina, T., Hropost, V., Babka, V., Hryshchenko, I. (2023). Determination of the form of a spiral spring in a free state. ScienceRise, 3, 3–9. https://doi.org/10.21303/2313-8416.2023.003213
- Pagani, A., Carrera, E. (2017). Large-deflection and post-buckling analyses of laminated composite beams by Carrera Unified Formulation. Composite Structures, 170, 40–52. https://doi.org/10.1016/j.compstruct.2017.03.008
- Ghuku, S., Saha, K. (2020). Large Deflection of Clamped Curved Beam Under Finite Clamping and Different Combinations of Bending-Stretching. Engineering Science & Technology, 121–134. https://doi.org/10.37256/est.212021548
- Wu, K., Zheng, G. (2022). Insight into numerical solutions of static large deflection of general planar beams for Compliant Mechanisms. Mechanism and Machine Theory, 172, 104757. https://doi.org/10.1016/j.mechmachtheory.2022.104757
- Wu, K., Zheng, G. (2021). Theoretical Analysis on Nonlinear Buckling, Post-Buckling of Slender Beams and Bi-Stable Mechanisms. Journal of Mechanisms and Robotics, 14 (3). https://doi.org/10.1115/1.4053047
- Eroglu, U. (2016). Large deflection analysis of planar curved beams made of Functionally Graded Materials using Variational Iterational Method. Composite Structures, 136, 204–216. https://doi.org/10.1016/j.compstruct.2015.10.017
- Nadykto, V. T., Tikhovod, M. A. (2020). Harrow section movement sustainability analysis. Naukovij Žurnal «Tehnìka Ta Energetika», 11 (2), 95–105. https://doi.org/10.31548/machenergy2020.02.095
- Gaponova, O., Kundera, Cz., Kirik, G., Tarelnyk, V., Martsynkovskyy, V., Konoplianchenko, Ie. et al. (2019). Estimating Qualitative Parameters of Aluminized Coating Obtained by Electric Spark Alloying Method. Advances in Thin Films, Nanostructured Materials, and Coatings, 249–266. https://doi.org/10.1007/978-981-13-6133-3_25
- Tarelnyk, V. B., Gaponova, O. P., Loboda, V. B., Konoplyanchenko, E. V., Martsinkovskii, V. S., Semirnenko, Yu. I. et al. (2021). Improving Ecological Safety when Forming Wear-Resistant Coatings on the Surfaces of Rotation Body Parts of 12Kh18N10T Steel Using a Combined Technology Based on Electrospark Alloying. Surface Engineering and Applied Electrochemistry, 57 (2), 173–184. https://doi.org/10.3103/s1068375521020113
- Wadi, K. J., Yadeem, J. M., Mustafa khazaal, S., Al-Ansari, L. S., Abdulsamad, H. J. (2022). Static deflection calculation for axially FG cantilever beam under uniformly distributed and transverse tip loads. Results in Engineering, 14, 100395. https://doi.org/10.1016/j.rineng.2022.100395
- Diwan, A. A., Al-Ansari, L. S., Al-Saffar, A. A., Al-Anssari, Q. S. (2019). Experimental and theoretical investigation of static deflection and natural frequency of stepped cantilever beam. Australian Journal of Mechanical Engineering, 20 (2), 303–315. https://doi.org/10.1080/14484846.2019.1704494
- Alansari, L. S., Abdulsamad, H. J., Wadi, K. J., Al-Raheem, S. Kh. (2021). Investigation of static deflection in internal stepped cantilever beam. Journal of Mechanical Engineering Research and Developments, 44 (5), 87–125.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Serhii Pylypaka, Victor Nesvidomin, Tetiana Volina, Iryna Hryshchenko, Taras Pylypaka, Yaroslav Kremets, Serhii Andrukh, Oleksandr Savoiskyi, Larysa Korzh-Usenko, Yuriy Semirnenko

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









