Devising a computer method to recognize and analyze spectrometric signals parameters

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.318558

Keywords:

computer analysis of spectrometric signals, digital signal filtering, computer simulation, recognition algorithms, fast discrete Fourier transform

Abstract

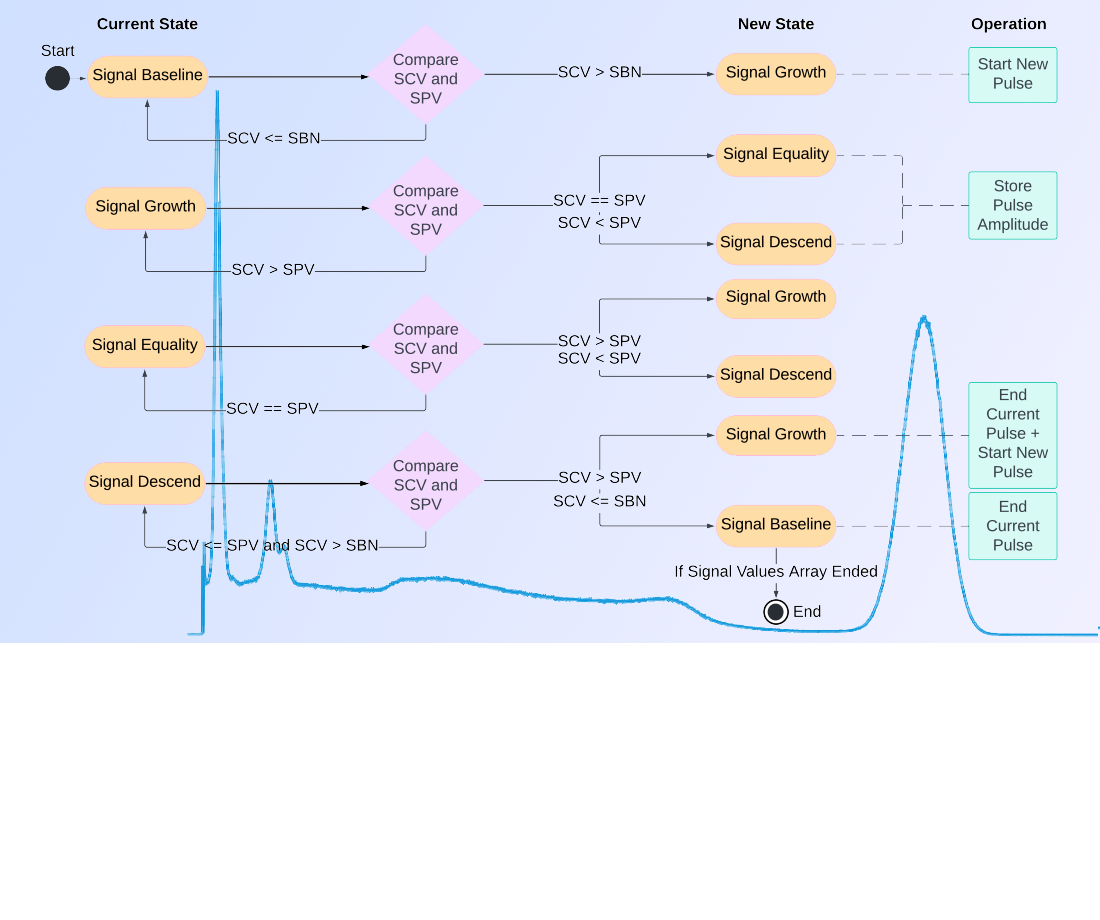
The object of this study is computerized systems for measuring the parameters of spectrometric signals digitized using special hardware. The task addressed in the research is to improve the process of filtering the usable pulse signal from noise and increase the accuracy of measuring pulse parameters by devising a new method of analysis. In order to verify the performance of the new method in comparison with several already known ones, input data arrays with predetermined parameters were prepared using computer simulation. A special algorithm was also developed to verify each detected pulse. As a result, the main characteristics of the methods, such as signal recognition accuracy and data processing speed, were obtained for several scenarios with different durations of modeling process and different pulse generation intensities. Comparative performance metrics were provided for all described software analysis methods. Ultimately, in the studied scenarios, the devised method showed better recognition ability than the considered alternative methods.

The key features of the proposed method are the use of software filters built on the basis of the application of Fast Discrete Fourier Transform (FDFT) algorithms and further computer processing of the signal using a mechanism for correcting the amplitudes of superimposed pulses. This makes it possible to filter the signal from noise without significantly changing the usable component and to more accurately determine the amplitudes in case of their frequent superposition. In practice, the devised method could be used to improve existing and design new computer systems of spectral analysis

Author Biographies

Sergiy Reva, V. N. Karazin Kharkiv National University

PhD

Department of Computer Systems and Robotics

Denys Tsybliyev, V. N. Karazin Kharkiv National University

PhD Student

Department of Computer Systems and Robotics

References

  1. Knoll, G. F. (2010). Radiation Detection and Measurement. John Wiley & Sons, 864.
  2. Wolszczak, W., Dorenbos, P. (2018). Time-resolved gamma spectroscopy of single events. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 886, 30–35. https://doi.org/10.1016/j.nima.2017.12.080
  3. Pollastrone, F., Cardarilli, G. C., Riva, M., Costa Pereira, R., Fernandes, A., Cruz, N. et al. (2019). A clustering algorithm for scintillator signals applied to neutron and gamma patterns identification. Fusion Engineering and Design, 146, 2110–2114. https://doi.org/10.1016/j.fusengdes.2019.03.117
  4. Lopatin, M., Moskovitch, N., Trigano, T., Sepulcre, Y. (2012). Pileup attenuation for spectroscopic signals using a sparse reconstruction. 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, 1–5. https://doi.org/10.1109/eeei.2012.6377045
  5. Khilkevitch, E. M., Shevelev, A. E., Chugunov, I. N., Iliasova, M. V., Doinikov, D. N., Gin, D. B. et al. (2020). Advanced algorithms for signal processing scintillation gamma ray detectors at high counting rates. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 977, 164309. https://doi.org/10.1016/j.nima.2020.164309
  6. Shevelev, A. E., Khilkevitch, E. M., Lashkul, S. I., Rozhdestvensky, V. V., Altukhov, A. B., Chugunov, I. N. et al. (2016). High performance gamma-ray spectrometer for runaway electron studies on the FT-2 tokamak. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 830, 102–108. https://doi.org/10.1016/j.nima.2016.05.075
  7. Yoon, S., Lee, C., Won, B.-H., Hong, S.-B., Seo, H., Kim, H.-D. (2022). Fast neutron-gamma discrimination in organic scintillators via convolution neural network. Journal of the Korean Physical Society, 80 (5), 427–433. https://doi.org/10.1007/s40042-022-00398-x
  8. Yoon, S., Lee, C., Seo, H., Kim, H.-D. (2023). Improved fast neutron detection using CNN-based pulse shape discrimination. Nuclear Engineering and Technology, 55 (11), 3925–3934. https://doi.org/10.1016/j.net.2023.07.007
  9. Law, A. M., Kelton, W. D. (2000). Simulation Modeling and Analysis. McGraw-Hill, 760.
  10. Reva, S., Tsybliyev, D. (2023). Mathematical models and algorithms of computer modeling of spectrometric signals. Bulletin of V. N. Karazin Kharkiv National University, Series «Mathematical Modeling. Information Technology. Automated Control Systems», 58, 64–74. Available at: https://periodicals.karazin.ua/mia/article/view/23502
  11. Meyers, S. (2014). Effective Modern C++: 42 Specific Ways to Improve Your Use of C++11 and C++14. O'Reilly Media, Inc. Addison-Wesley, 320.
  12. Drozdek, A. (2001). Data Structures and Algorithms in C++. Brooks/Cole, 650.
  13. QT Framework Official Website. Available at: https://www.qt.io/product/framework
  14. Wahab, M. F., Gritti, F., O’Haver, T. C. (2021). Discrete Fourier transform techniques for noise reduction and digital enhancement of analytical signals. TrAC Trends in Analytical Chemistry, 143, 116354. https://doi.org/10.1016/j.trac.2021.116354
  15. Bracewell, R. N. (2000). The Fourier Transform and its Applications. New Delhi: McGraw-Hill Education, 640.
  16. Heideman, M. T., Johnson, D. H., Burrus, C. S. (1985). Gauss and the history of the fast Fourier transform. Archive for History of Exact Sciences, 34 (3), 265–277. https://doi.org/10.1007/bf00348431
  17. Press, W., Teukolsky, S., Vetterling, W., Flannery, B. (2007). Numerical recipes. The Art of Scientific Computing. Cambridge University Press, 1256. Available at: https://www.cambridge.org/us/universitypress/subjects/mathematics/numerical-recipes/numerical-recipes-art-scientific-computing-3rd-edition
  18. OMG Unified Modeling Language Specification. Version 2.5 (2015). Available at: https://www.omg.org/spec/UML/2.5/PDF
  19. Larman, C. (2004). Applying UML and Patterns: An Introduction to Object-Oriented Analysis and Design and Iterative Development. Addison Wesley Professional, 736.
Devising a computer method to recognize and analyze spectrometric signals parameters

Downloads

Published

2024-12-27

How to Cite

Reva, S., & Tsybliyev, D. (2024). Devising a computer method to recognize and analyze spectrometric signals parameters. Eastern-European Journal of Enterprise Technologies, 6(9 (132), 86–96. https://doi.org/10.15587/1729-4061.2024.318558

Issue

Vol. 6 No. 9 (132) (2024): Information and controlling system

Section

Information and controlling system

License

Copyright (c) 2024 Sergiy Reva, Denys Tsybliyev

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.