Розробка комп’ютерного методу розпізнавання та аналізу параметрів спектрометричних сигналів
DOI:
https://doi.org/10.15587/1729-4061.2024.318558Ключові слова:
комп’ютерний аналіз спектрометричних сигналів, цифрова фільтрація сигналів, комп’ютерне моделювання, алгоритми розпізнавання, швидке дискретне перетворення Фур’єАнотація
Об’єктом дослідження є комп’ютеризовані системи для вимірювання параметрів спектрометричних сигналів, оцифрованих за допомогою спеціальних апаратних засобів. Проблема, що вирішувалася в рамках дослідження, – це вдосконалення процесу фільтрації корисного імпульсного сигналу від шуму та підвищення точності вимірювання параметрів імпульсів шляхом розробки нового методу аналізу. Для перевірки роботи розробленого методу у порівнянні із кількома вже відомими за допомогою комп’ютерного моделювання були підготовлені масиви вхідних числових даних із наперед визначеними параметрами. Також був розроблений спеціальний алгоритм верифікації кожного розпізнаного імпульсу. В результаті були отримані основні характеристики методів, такі як точність розпізнавання сигналів та швидкість обробки даних, для кількох сценаріїв з різною тривалістю процесу моделювання та різним рівнем завантаження. Наведено порівняльні метрики ефективності для всіх описаних методів програмного аналізу. В підсумку, серед досліджених сценаріїв розроблений метод показав кращу розпізнавальну здатність, ніж розглянуті альтернативні методи.
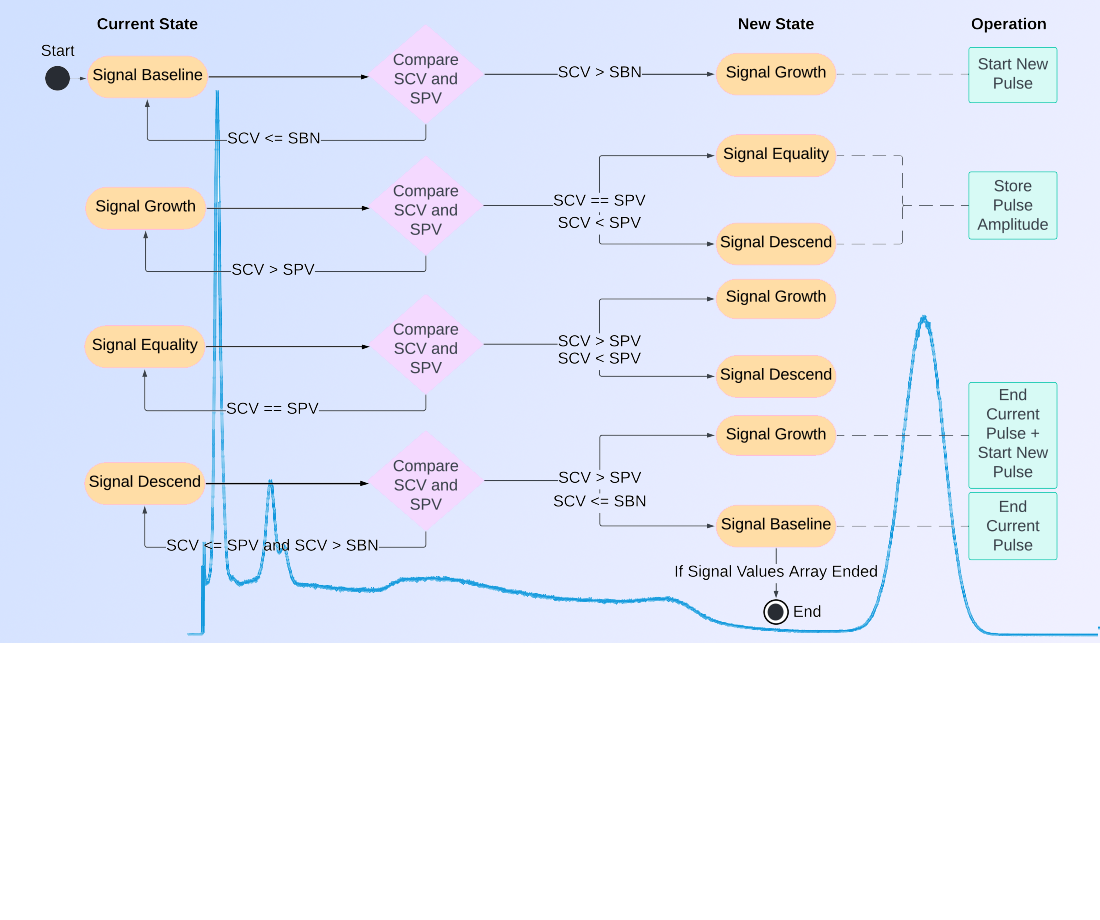
Особливостями запропонованого методу є використання програмних фільтрів, побудованих на основі застосування алгоритмів Fast Discrete Fourier Transform (FDFT) та подальша комп’ютерна обробка сигналу із використанням механізму корекції амплітуд імпульсів, що накладаються один на одного. Це дозволяє здійснювати фільтрацію сигналу від шуму без суттєвої зміни корисної складової і точніше визначати амплітуди імпульсів при їх частій суперпозиції. На практиці розроблений метод може бути використаний для вдосконалення існуючих та розробки нових комп’ютерних систем спектрального аналізу.
Посилання
- Knoll, G. F. (2010). Radiation Detection and Measurement. John Wiley & Sons, 864.
- Wolszczak, W., Dorenbos, P. (2018). Time-resolved gamma spectroscopy of single events. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 886, 30–35. https://doi.org/10.1016/j.nima.2017.12.080
- Pollastrone, F., Cardarilli, G. C., Riva, M., Costa Pereira, R., Fernandes, A., Cruz, N. et al. (2019). A clustering algorithm for scintillator signals applied to neutron and gamma patterns identification. Fusion Engineering and Design, 146, 2110–2114. https://doi.org/10.1016/j.fusengdes.2019.03.117
- Lopatin, M., Moskovitch, N., Trigano, T., Sepulcre, Y. (2012). Pileup attenuation for spectroscopic signals using a sparse reconstruction. 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, 1–5. https://doi.org/10.1109/eeei.2012.6377045
- Khilkevitch, E. M., Shevelev, A. E., Chugunov, I. N., Iliasova, M. V., Doinikov, D. N., Gin, D. B. et al. (2020). Advanced algorithms for signal processing scintillation gamma ray detectors at high counting rates. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 977, 164309. https://doi.org/10.1016/j.nima.2020.164309
- Shevelev, A. E., Khilkevitch, E. M., Lashkul, S. I., Rozhdestvensky, V. V., Altukhov, A. B., Chugunov, I. N. et al. (2016). High performance gamma-ray spectrometer for runaway electron studies on the FT-2 tokamak. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 830, 102–108. https://doi.org/10.1016/j.nima.2016.05.075
- Yoon, S., Lee, C., Won, B.-H., Hong, S.-B., Seo, H., Kim, H.-D. (2022). Fast neutron-gamma discrimination in organic scintillators via convolution neural network. Journal of the Korean Physical Society, 80 (5), 427–433. https://doi.org/10.1007/s40042-022-00398-x
- Yoon, S., Lee, C., Seo, H., Kim, H.-D. (2023). Improved fast neutron detection using CNN-based pulse shape discrimination. Nuclear Engineering and Technology, 55 (11), 3925–3934. https://doi.org/10.1016/j.net.2023.07.007
- Law, A. M., Kelton, W. D. (2000). Simulation Modeling and Analysis. McGraw-Hill, 760.
- Reva, S., Tsybliyev, D. (2023). Mathematical models and algorithms of computer modeling of spectrometric signals. Bulletin of V. N. Karazin Kharkiv National University, Series «Mathematical Modeling. Information Technology. Automated Control Systems», 58, 64–74. Available at: https://periodicals.karazin.ua/mia/article/view/23502
- Meyers, S. (2014). Effective Modern C++: 42 Specific Ways to Improve Your Use of C++11 and C++14. O'Reilly Media, Inc. Addison-Wesley, 320.
- Drozdek, A. (2001). Data Structures and Algorithms in C++. Brooks/Cole, 650.
- QT Framework Official Website. Available at: https://www.qt.io/product/framework
- Wahab, M. F., Gritti, F., O’Haver, T. C. (2021). Discrete Fourier transform techniques for noise reduction and digital enhancement of analytical signals. TrAC Trends in Analytical Chemistry, 143, 116354. https://doi.org/10.1016/j.trac.2021.116354
- Bracewell, R. N. (2000). The Fourier Transform and its Applications. New Delhi: McGraw-Hill Education, 640.
- Heideman, M. T., Johnson, D. H., Burrus, C. S. (1985). Gauss and the history of the fast Fourier transform. Archive for History of Exact Sciences, 34 (3), 265–277. https://doi.org/10.1007/bf00348431
- Press, W., Teukolsky, S., Vetterling, W., Flannery, B. (2007). Numerical recipes. The Art of Scientific Computing. Cambridge University Press, 1256. Available at: https://www.cambridge.org/us/universitypress/subjects/mathematics/numerical-recipes/numerical-recipes-art-scientific-computing-3rd-edition
- OMG Unified Modeling Language Specification. Version 2.5 (2015). Available at: https://www.omg.org/spec/UML/2.5/PDF
- Larman, C. (2004). Applying UML and Patterns: An Introduction to Object-Oriented Analysis and Design and Iterative Development. Addison Wesley Professional, 736.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Sergiy Reva, Denys Tsybliyev

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.










