Development of post-quantum cryptosystems based on the Rao-Nam scheme

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.323195

Keywords:

Rao-Nam crypto-code constructions, algebraic codes, intelligent protection systems

Abstract

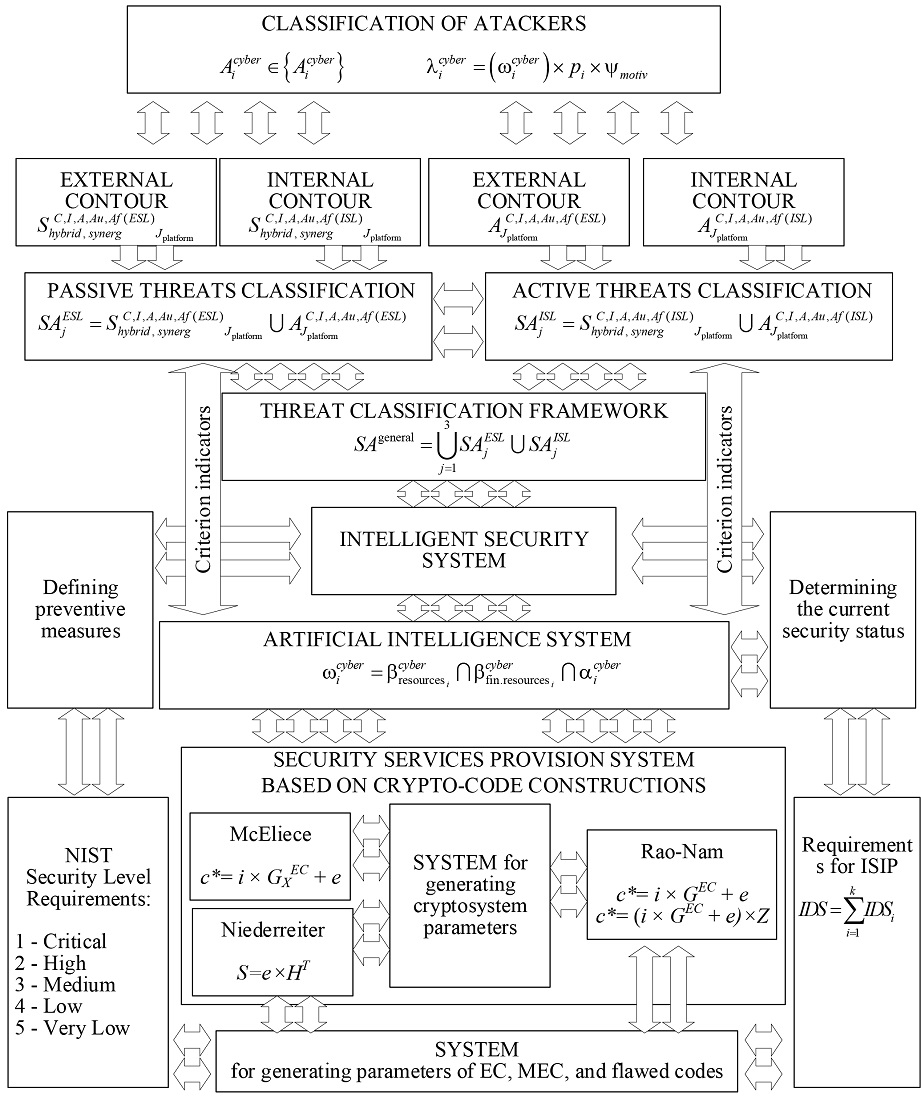
The object of the research is the process of ensuring the protection of data transmission in communication channels of critical infrastructure objects based on mobile and smart technologies. The development of quantum computing technologies based on Grover and Shor algorithms provides practical cracking of symmetric and asymmetric cryptosystems in polynomial time. The emergence of systems based on artificial intelligence allows creating hybrid systems for detecting weaknesses (critical points) in security systems not only on critical infrastructure objects. In addition, a full-scale quantum computer will open a new era of implementing post-quantum cryptography algorithms. Among the winners of post-quantum algorithms, the crypto-code constructions (CCC) of McEliece and Niederreiter are separately highlighted, which allow to provide the required level of protection and the required level of reliability of information transmission in an integrated manner. But a significant drawback is the possibility of cracking such systems on linear codes, as well as the need to build them on the Galois field 210–213, which significantly reduces their use in low-capacity systems based on smart and mobile technologies. To solve this drawback, the work proposes the use of a symmetric CCC based on the Rao-Nam scheme on algebrogeometric and flawed codes, which provides the possibility of significantly reducing the volume of key data (construction of CCC over the Galois field 24–26). When using the Rao-Nam CCC, a quantum symmetric algorithm is formed, which ensures the preservation of the level of stability and reliability of information transmission (safe time 1025–1035). This approach provides the possibility of forming intelligent information protection systems (IIPS). The given structural scheme of the IIPS construction ensures timely detection of threats with an assessment of the computational and financial and human capabilities of attackers, as well as the use of the necessary CCC/algebraic (flawed) codes to ensure the required level of security

Author Biographies

Yevhen Melenti, National Academy of the Security Service of Ukraine

PhD, Associate Professor

First Vice-Rector

Olha Korol, National Technical University “Kharkiv Polytechnic Institute”

PhD, Associate Professor

Department of Cybersecurity

Volodymyr Shulha, State University of Information and Communication Technologies

Doctor of Historical Sciences, Senior Researcher

Rector

Stanislav Milevskyi, National Technical University “Kharkiv Polytechnic Institute”

PhD, Associate Professor

Department of Cybersecurity

Оleksandr Sievierinov, Kharkiv National University of Radio Electronics

PhD, Associate Professor

Department of Information Technology Security

Oleksandr Voitko, National Defence University of Ukraine

PhD, Associate Professor

Head of the Institute

Strategic Communications Institute

Khazail Rzayev, Azerbaijan Technical University

Doctor of Technical Sciences, Associate Professor

Department of Computer Technologies

Iryna Husarova, Kharkiv National University of Radio Electronics

PhD, Associate Professor, Professor

Department of Applied Mathematics

Serhii Kravchenko, National Defence University of Ukraine

PhD, Associate Professor

Department of Land Forces

Sevinj Pashayeva, Nakhchivan State University

Senior Lecturer

Department of Informatics

References

  1. Rose, S., Borchert, O., Mitchell, S., Connelly, S. (2020). Zero Trust Architecture. NIST Special Publication 800-207. National Institute of Standards and Technology. https://doi.org/10.6028/nist.sp.800-207
  2. Yevseiev, S., Melenti, Y., Voitko, O., Hrebeniuk, V., Korchenko, A., Mykus, S. et al. (2021). Development of a concept for building a critical infrastructure facilities security system. Eastern-European Journal of Enterprise Technologies, 3 (9 (111)), 63–83. https://doi.org/10.15587/1729-4061.2021.233533
  3. Petrivskyi, V., Shevchenko, V., Yevseiev, S., Milov, O., Laptiev, O., Bychkov, O. et al. (2022). Development of a modification of the method for constructing energy-efficient sensor networks using static and dynamic sensors. Eastern-European Journal of Enterprise Technologies, 1 (9 (115)), 15–23. https://doi.org/10.15587/1729-4061.2022.252988
  4. Yevseiev, S., Milevskyi, S., Bortnik, L., Alexey, V., Bondarenko, K., Pohasii, S. (2022). Socio-Cyber-Physical Systems Security Concept. 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), 1–8. https://doi.org/10.1109/hora55278.2022.9799957
  5. Bernstein, D. J. (2009). Introduction to post-quantum cryptography. Post-Quantum Cryptography, 1–14. https://doi.org/10.1007/978-3-540-88702-7_1
  6. Grassl, M., Langenberg, B., Roetteler, M., Steinwandt, R. (2016). Applying Grover’s Algorithm to AES: Quantum Resource Estimates. Post-Quantum Cryptography, 29–43. https://doi.org/10.1007/978-3-319-29360-8_3
  7. Amy, M., Di Matteo, O., Gheorghiu, V., Mosca, M., Parent, A., Schanck, J. (2017). Estimating the Cost of Generic Quantum Pre-image Attacks on SHA-2 and SHA-3. Selected Areas in Cryptography – SAC 2016, 317–337. https://doi.org/10.1007/978-3-319-69453-5_18
  8. Chen, L., Jordan, S., Liu, Y.-K., Moody, D., Peralta, R., Perlner, R., Smith-Tone, D. (2016). Report on Post-Quantum Cryptography. National Institute of Standards and Technology. https://doi.org/10.6028/nist.ir.8105
  9. Mariantoni, M. (2014). Building a Superconducting Quantum Computer. Available at: https://www.youtube.com/watch?v=wWHAs--HA1c
  10. Xu, N., Zhu, J., Lu, D., Zhou, X., Peng, X., Du, J. (2012). Quantum Factorization of 143 on a Dipolar-Coupling Nuclear Magnetic Resonance System. Physical Review Letters, 108 (13). https://doi.org/10.1103/physrevlett.108.130501
  11. Dattani, N. S., Bryans, N. (2014). Quantum factorization of 56153 with only 4 qubits. arXiv. https://doi.org/10.48550/arXiv.1411.6758
  12. McEliece, R. J. (1978). A public-key cryptosystem based on algebraic coding theory. DSN progress report 42-44, 114–116. Available at: https://ipnpr.jpl.nasa.gov/progress_report/42-44/44N.PDF
  13. Niederreiter, H. (1986). Knapsack-Type Cryptosystems and Algebraic Coding Theory. Problems of Control and Information Theory, 15 (2), 19–34.
  14. Rao, T. R. N., Nam, K.-H. (1987). Private-Key Algebraic-Coded Cryptosystems. Advances in Cryptology – CRYPTO’ 86, 35–48. https://doi.org/10.1007/3-540-47721-7_3
  15. Struik, R., van Tilburg, J. (1988). The Rao-Nam Scheme is Insecure Against a Chosen-Plaintext Attack. Advances in Cryptology – CRYPTO ’87, 445–457. https://doi.org/10.1007/3-540-48184-2_40
  16. Cheng, Y. C., Lu, E. H., Wu, S. W. (1998). A modified version of the Rao-Nam algebraic-code encryption scheme. Information Processing Letters, 68 (4), 215–217. https://doi.org/10.1016/s0020-0190(98)00156-2
  17. Li, Y. X., Deng, R. H., Wang, X. M. (1994). On the equivalence of McEliece’s and Niederreiter’s public-key cryptosystems. IEEE Transactions on Information Theory, 40 (1), 271–273. https://doi.org/10.1109/18.272496
  18. Bernstein, D. J. (2010). Grover vs. McEliece. Post-Quantum Cryptography, 73–80. https://doi.org/10.1007/978-3-642-12929-2_6
  19. Sidelnikov, V. M. (1994). A public-key cryptosystem based on binary Reed-Muller codes. Discrete Mathematics and Applications, 4 (3). https://doi.org/10.1515/dma.1994.4.3.191
  20. Minder, L., Shokrollahi, A. (2007). Cryptanalysis of the Sidelnikov Cryptosystem. Advances in Cryptology - EUROCRYPT 2007, 347–360. https://doi.org/10.1007/978-3-540-72540-4_20
  21. Baldi, M., Chiaraluce, F. (2007). Cryptanalysis of a new instance of McEliece cryptosystem based on QC-LDPC Codes. 2007 IEEE International Symposium on Information Theory, 2591–2595. https://doi.org/10.1109/isit.2007.4557609
  22. Liu, J., Tong, X., Wang, Z., Ma, J., Yi, L. (2019). An Improved Rao–Nam Cryptosystem Based on Fractional Order Hyperchaotic System and EDF–QC–LDPC. International Journal of Bifurcation and Chaos, 29 (09), 1950122. https://doi.org/10.1142/s0218127419501220
  23. Yevseiev, S., Rzayev, K., Korol, O., Imanova, Z. (2016). Development of mceliece modified asymmetric crypto-code system on elliptic truncated codes. Eastern-European Journal of Enterprise Technologies, 4 (9 (82)), 18–26. https://doi.org/10.15587/1729-4061.2016.75250
  24. Yevseiev, S., Tsyhanenko, O., Ivanchenko, S., Aleksiyev, V., Verheles, D., Volkov, S. et al. (2018). Practical implementation of the Niederreiter modified crypto­code system on truncated elliptic codes. Eastern-European Journal of Enterprise Technologies, 6 (4 (96)), 24–31. https://doi.org/10.15587/1729-4061.2018.150903
  25. Yevseiev, S., Hryhorii, K., Liekariev, Y. (2016). Developing of multi-factor authentication method based on niederreiter-mceliece modified crypto-code system. Eastern-European Journal of Enterprise Technologies, 6 (4 (84)), 11–23. https://doi.org/10.15587/1729-4061.2016.86175
  26. Couvreur, A., Otmani, A., Tillich, J. (2014). Polynomial Time Attack on Wild McEliece over Quadratic Extensions. Advances in Cryptology – EUROCRYPT 2014, 17–39. https://doi.org/10.1007/978-3-642-55220-5_2
  27. Yevseiev, S., Korol, O., Kots, H. (2017). Construction of hybrid security systems based on the crypto-code structures and flawed codes. Eastern-European Journal of Enterprise Technologies, 4 (9 (88)), 4–21. https://doi.org/10.15587/1729-4061.2017.108461
  28. Yevseiev, S., Tsyhanenko, O., Gavrilova, A., Guzhva, V., Milov, O., Moskalenko, V. et al. (2019). Development of Niederreiter hybrid crypto-code structure on flawed codes. Eastern-European Journal of Enterprise Technologies, 1 (9 (97)), 27–38. https://doi.org/10.15587/1729-4061.2019.156620
  29. Zhang, G., Cai, S. (2017). Universal secure error-correcting (SEC) schemes for network coding via McEliece cryptosystem based on QC-LDPC codes. Cluster Computing, 22 (S2), 2599–2610. https://doi.org/10.1007/s10586-017-1354-x
  30. Baldi, M., Bianchi, M., Chiaraluce, F., Rosenthal, J., Schipani, D. (2014). Enhanced Public Key Security for the McEliece Cryptosystem. Journal of Cryptology, 29 (1), 1–27. https://doi.org/10.1007/s00145-014-9187-8
  31. Moufek, H., Guenda, K. (2017). A New variant of the McEliece cryptosystem based on the Smith form of convolutional codes. Cryptologia, 42 (3), 227–239. https://doi.org/10.1080/01611194.2017.1362061
  32. Dinh, H., Moore, C., Russell, A. (2011). McEliece and Niederreiter Cryptosystems That Resist Quantum Fourier Sampling Attacks. Advances in Cryptology – CRYPTO 2011, 761–779. https://doi.org/10.1007/978-3-642-22792-9_43
  33. Tsyhanenko, O., Rzayev, K., Mammadova, T. (2018). Mathematical model of the modified niederreiter crypto-code structures. Advanced Information Systems, 2 (4), 37–44. https://doi.org/10.20998/2522-9052.2018.4.06
  34. Massey, J. L. (1986). Theory and practice of error control codes. Proceedings of the IEEE, 74 (9), 1293–1294. https://doi.org/10.1109/proc.1986.13626
  35. Mishenko, V. A., Vilanskiy, Yu. V. (2007). Usherbnye teksty i mnogokanalnaya kriptografiya. Minsk: Enciklopediks.
  36. Mishenko, V. A., Vilanskiy, Yu. V., Lepin, V. V (2007). Kriptograficheskiy algoritm MV2. Minsk: Enciklopediks.
  37. Yevseiev, S. (2017). The use of damaged codes in crypto code systems. Systemy obrobky informatsiyi, 5, 109–121. Available at: http://nbuv.gov.ua/UJRN/soi_2017_5_17
  38. Voronin, A., Akhiiezer, O., Galuza, A., Lebedeva, I., Zaitsev, Y., Lebedev, S. (2023). Modeling Competitive Interaction “Predator-Prey” on the Example of Two Innovative Processes. 2023 13th International Conference on Advanced Computer Information Technologies (ACIT), 131–134. https://doi.org/10.1109/acit58437.2023.10275538
  39. Rukhin, A., Sota, J., Nechvatal, J., Smid, M., Barker, E., Leigh, S. et al. (2000). A statistical test suite for random and pseudorandom number generators for cryptographic applications. National Institute of Standards and Technology. NIST Special Publication 800-22. https://doi.org/10.6028/nist.sp.800-22
  40. Potіj, O. V. (2004). Metodika statistichnogo testuvannja NIST STS ta matematichne obґruntuvannja testіv. Tehnіchnij zvіt ІІT – 001-2004. Kharkiv, 62.
  41. Класифікатор кібербезпеки. Available at: https://skl.khpi.edu.ua/
  42. Shmatko, O., Balakireva, S., Vlasov, A., Zagorodna, N., Korol, O., Milov, O. et al. (2020). Development of methodological foundations for designing a classifier of threats to cyberphysical systems. Eastern-European Journal of Enterprise Technologies, 3 (9 (105)), 6–19. https://doi.org/10.15587/1729-4061.2020.205702
  43. Yevseiev, S., Khokhlachova, Yu., Ostapov, S., Laptiev, O., Korol, O., Milevskyi, S. et al.; Yevseiev, S., Khokhlachova, Yu., Ostapov, S., Laptiev, O. (Eds.) (2023). Models of socio-cyber-physical systems security. Kharkiv: РС ТЕСHNOLOGY СЕNTЕR, 184. https://doi.org/10.15587/978-617-7319-72-5
  44. Avinash, S. V. (2017). Understanding Activation Functions in Neural Networks. The Theory Of Everything. Available at: https://medium.com/the-theory-of-everything/understanding-activation- functions-in-neural-networks-9491262884e0
  45. AutoDraw. Available at: https://www.autodraw.com/
  46. Kreutz, D., Ramos, F. M. V., Esteves Verissimo, P., Esteve Rothenberg, C., Azodolmolky, S., Uhlig, S. (2015). Software-Defined Networking: A Comprehensive Survey. Proceedings of the IEEE, 103 (1), 14–76. https://doi.org/10.1109/jproc.2014.2371999
  47. Geetha, R., Thilagam, T. (2020). A Review on the Effectiveness of Machine Learning and Deep Learning Algorithms for Cyber Security. Archives of Computational Methods in Engineering, 28 (4), 2861–2879. https://doi.org/10.1007/s11831-020-09478-2
  48. Salvakkam, D. B., Saravanan, V., Jain, P. K., Pamula, R. (2023). Enhanced Quantum-Secure Ensemble Intrusion Detection Techniques for Cloud Based on Deep Learning. Cognitive Computation, 15 (5), 1593–1612. https://doi.org/10.1007/s12559-023-10139-2
  49. Tavallaee, M., Bagheri, E., Lu, W., Ghorbani, A. A. (2009). A detailed analysis of the KDD CUP 99 data set. 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, 1–6. https://doi.org/10.1109/cisda.2009.5356528
Development of post-quantum cryptosystems based on the Rao-Nam scheme

Downloads

Published

2025-02-28

How to Cite

Melenti, Y., Korol, O., Shulha, V., Milevskyi, S., Sievierinov О., Voitko, O., Rzayev, K., Husarova, I., Kravchenko, S., & Pashayeva, S. (2025). Development of post-quantum cryptosystems based on the Rao-Nam scheme. Eastern-European Journal of Enterprise Technologies, 1(9 (133), 35–48. https://doi.org/10.15587/1729-4061.2025.323195

Issue

Vol. 1 No. 9 (133) (2025): Information and controlling system

Section

Information and controlling system

License

Copyright (c) 2025 Yevhen Melenti, Olha Korol, Volodymyr Shulha, Stanislav Milevskyi, Оleksandr Sievierinov, Oleksandr Voitko, Khazail Rzayev, Iryna Husarova, Serhii Kravchenko, Sevinj Pashayeva

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.