Розробка постквантових криптосистем на основі схеми Рао-Нама

Автор(и)

DOI:

https://doi.org/10.15587/1729-4061.2025.323195

Ключові слова:

крипто-кодові конструкції Рао-Нама, алгебраїчні коди, інтелектуальні системи захисту

Анотація

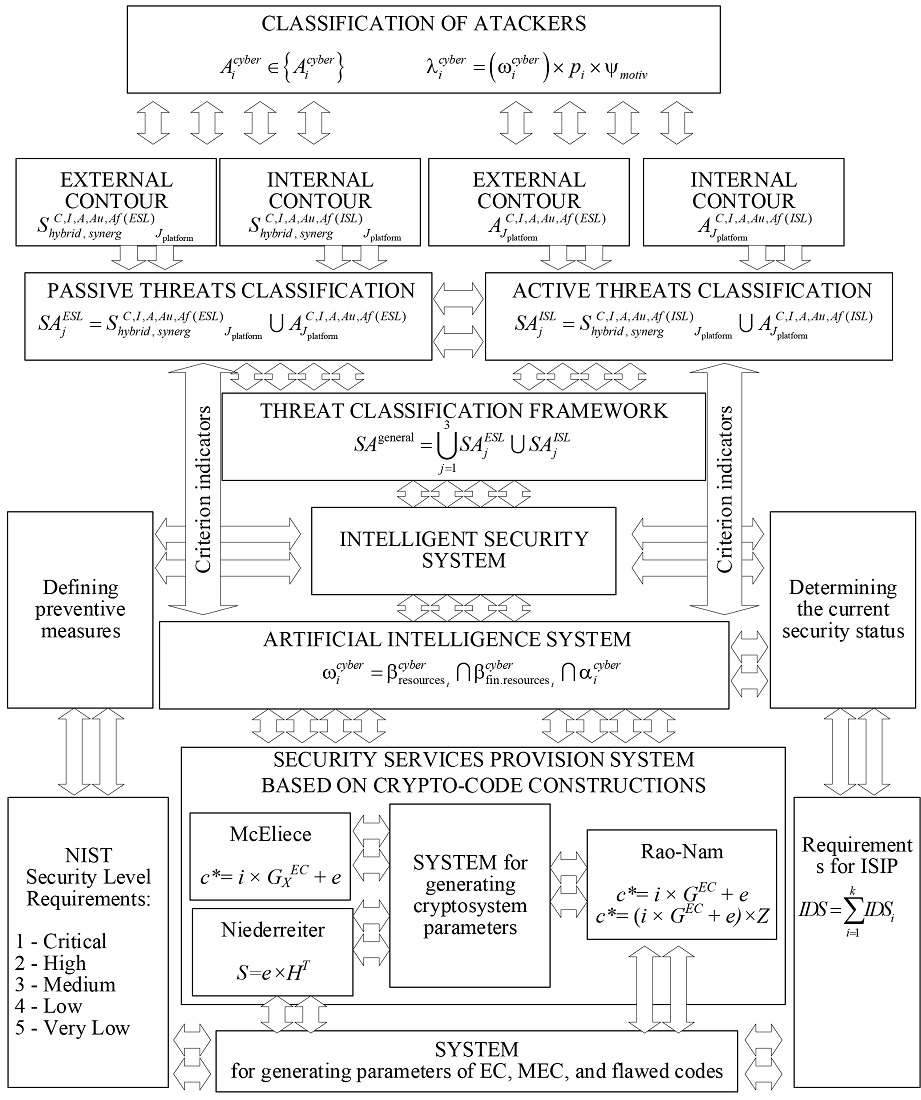
Об’єктом дослідження є процес забезпечення захисту передачі даних в каналах зв’язку об’єктів критичної інфраструктури на основі мобільних та смарт-технологій. Розвиток технологій квантових обчислень на основі алгоритмів Гровера та Шора забезпечують практичний злам симетричних та несиметричних криптосистем за поліноміальний час. Поява систем на основі штучного інтелекту дозволяють створювати гібридні системи виявлення слабких місць (критичних точок) у системах безпеки не тільки об’єктів критичної інфраструктури. Крім цього повномасштабний квантовий комп’ютер відкриє нову еру впровадження алгоритмів постквантової криптографії. Серед переможців постквантових алгоритмів окремо виділені крипто-кодові конструкції (ККК) Мак-Еліса та Нідерайтера, які дозволяють інтегровано забезпечити необхідний рівень захисту та інтегровано забезпечити необхідний рівень вірогідності передачі інформації. Але суттєвим недоліком є можливість зламу таких систем на лінійних кодах, а також необхідність їх побудови на полем Галуа 210–213, що суттєво зменшує їх використання в низькоємних системах на основі смарт- та мобільних технологій. Для розв’язання цього недоліку у роботі пропонується використання симетричної ККК на основі схеми Рао-Нама на алгеброгеометричних та збиткових кодах, що забезпечує можливість забезпечить значного зменшення об’єму ключових даних (побудова ККК над полем на Галуа 24–26). При використанні ККК Рао-Нама формується квантовий симетричний алгоритм, який забезпечує зберігання рівня стійкості та вірогідності передачі інформації (безпечний час 1025–1035). Такий підхід забезпечує можливість формування інтелектуальних систем захисту інформації (ІСЗІ). Наведена структурна схема побудови ІСЗІ забезпечує своєчасне виявлення загроз з оцінкою обчислювальних та фінансово-людських можливостей нападників, а також використання необхідних ККК/алгебраїчних (збиткових) кодів для забезпечення необхідного рівня безпеки

Біографії авторів

Євген Олександрович Меленті, Національна академія Служби безпеки України

Кандидат технічних наук, доцент

Перший проректор

Ольга Григорівна Король, Національний технічний університет “Харківський політехнічний інститут”

Кандидат технічних наук, доцент

Кафедра кібербезпеки

Володимир Петрович Шульга, Державний університет інформаційно-комунікаційних технологій

Доктор історичних наук, старший дослідник

Ректор

Станіслав Валерійович Мілевський, Національний технічний університет “Харківський політехнічний інститут”

Кандидат економічних наук, доцент

Кафедра кібербезпеки

Олександр Васильович Сєвєрінов, Харківський національний університет радіоелектроніки

Кандидат технічних наук, доцент

Кафедра безпеки інформаційних технологій

Олександр Володимирович Войтко, Національний університет оборони України

Кандидат військових наук, доцент

Начальник інституту

Інститут стратегічних комунікацій

Khazail Rzayev, Azerbaijan Technical University

Doctor of Technical Sciences, Associate Professor

Department of Computer Technologies

Ірина Григоріївна Гусарова, Харківський національний університет радіоелектроніки

Кандидат технічних наук, доцент, професор

Кафедра прикладної математики

Сергій Опанасович Кравченко, Національний університет оборони України

Кандидат військових наук, доцент

Кафедра сухопутних військ

Sevinj Pashayeva, Nakhchivan State University

Senior Lecturer

Department of Informatics

Посилання

  1. Rose, S., Borchert, O., Mitchell, S., Connelly, S. (2020). Zero Trust Architecture. NIST Special Publication 800-207. National Institute of Standards and Technology. https://doi.org/10.6028/nist.sp.800-207
  2. Yevseiev, S., Melenti, Y., Voitko, O., Hrebeniuk, V., Korchenko, A., Mykus, S. et al. (2021). Development of a concept for building a critical infrastructure facilities security system. Eastern-European Journal of Enterprise Technologies, 3 (9 (111)), 63–83. https://doi.org/10.15587/1729-4061.2021.233533
  3. Petrivskyi, V., Shevchenko, V., Yevseiev, S., Milov, O., Laptiev, O., Bychkov, O. et al. (2022). Development of a modification of the method for constructing energy-efficient sensor networks using static and dynamic sensors. Eastern-European Journal of Enterprise Technologies, 1 (9 (115)), 15–23. https://doi.org/10.15587/1729-4061.2022.252988
  4. Yevseiev, S., Milevskyi, S., Bortnik, L., Alexey, V., Bondarenko, K., Pohasii, S. (2022). Socio-Cyber-Physical Systems Security Concept. 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), 1–8. https://doi.org/10.1109/hora55278.2022.9799957
  5. Bernstein, D. J. (2009). Introduction to post-quantum cryptography. Post-Quantum Cryptography, 1–14. https://doi.org/10.1007/978-3-540-88702-7_1
  6. Grassl, M., Langenberg, B., Roetteler, M., Steinwandt, R. (2016). Applying Grover’s Algorithm to AES: Quantum Resource Estimates. Post-Quantum Cryptography, 29–43. https://doi.org/10.1007/978-3-319-29360-8_3
  7. Amy, M., Di Matteo, O., Gheorghiu, V., Mosca, M., Parent, A., Schanck, J. (2017). Estimating the Cost of Generic Quantum Pre-image Attacks on SHA-2 and SHA-3. Selected Areas in Cryptography – SAC 2016, 317–337. https://doi.org/10.1007/978-3-319-69453-5_18
  8. Chen, L., Jordan, S., Liu, Y.-K., Moody, D., Peralta, R., Perlner, R., Smith-Tone, D. (2016). Report on Post-Quantum Cryptography. National Institute of Standards and Technology. https://doi.org/10.6028/nist.ir.8105
  9. Mariantoni, M. (2014). Building a Superconducting Quantum Computer. Available at: https://www.youtube.com/watch?v=wWHAs--HA1c
  10. Xu, N., Zhu, J., Lu, D., Zhou, X., Peng, X., Du, J. (2012). Quantum Factorization of 143 on a Dipolar-Coupling Nuclear Magnetic Resonance System. Physical Review Letters, 108 (13). https://doi.org/10.1103/physrevlett.108.130501
  11. Dattani, N. S., Bryans, N. (2014). Quantum factorization of 56153 with only 4 qubits. arXiv. https://doi.org/10.48550/arXiv.1411.6758
  12. McEliece, R. J. (1978). A public-key cryptosystem based on algebraic coding theory. DSN progress report 42-44, 114–116. Available at: https://ipnpr.jpl.nasa.gov/progress_report/42-44/44N.PDF
  13. Niederreiter, H. (1986). Knapsack-Type Cryptosystems and Algebraic Coding Theory. Problems of Control and Information Theory, 15 (2), 19–34.
  14. Rao, T. R. N., Nam, K.-H. (1987). Private-Key Algebraic-Coded Cryptosystems. Advances in Cryptology – CRYPTO’ 86, 35–48. https://doi.org/10.1007/3-540-47721-7_3
  15. Struik, R., van Tilburg, J. (1988). The Rao-Nam Scheme is Insecure Against a Chosen-Plaintext Attack. Advances in Cryptology – CRYPTO ’87, 445–457. https://doi.org/10.1007/3-540-48184-2_40
  16. Cheng, Y. C., Lu, E. H., Wu, S. W. (1998). A modified version of the Rao-Nam algebraic-code encryption scheme. Information Processing Letters, 68 (4), 215–217. https://doi.org/10.1016/s0020-0190(98)00156-2
  17. Li, Y. X., Deng, R. H., Wang, X. M. (1994). On the equivalence of McEliece’s and Niederreiter’s public-key cryptosystems. IEEE Transactions on Information Theory, 40 (1), 271–273. https://doi.org/10.1109/18.272496
  18. Bernstein, D. J. (2010). Grover vs. McEliece. Post-Quantum Cryptography, 73–80. https://doi.org/10.1007/978-3-642-12929-2_6
  19. Sidelnikov, V. M. (1994). A public-key cryptosystem based on binary Reed-Muller codes. Discrete Mathematics and Applications, 4 (3). https://doi.org/10.1515/dma.1994.4.3.191
  20. Minder, L., Shokrollahi, A. (2007). Cryptanalysis of the Sidelnikov Cryptosystem. Advances in Cryptology - EUROCRYPT 2007, 347–360. https://doi.org/10.1007/978-3-540-72540-4_20
  21. Baldi, M., Chiaraluce, F. (2007). Cryptanalysis of a new instance of McEliece cryptosystem based on QC-LDPC Codes. 2007 IEEE International Symposium on Information Theory, 2591–2595. https://doi.org/10.1109/isit.2007.4557609
  22. Liu, J., Tong, X., Wang, Z., Ma, J., Yi, L. (2019). An Improved Rao–Nam Cryptosystem Based on Fractional Order Hyperchaotic System and EDF–QC–LDPC. International Journal of Bifurcation and Chaos, 29 (09), 1950122. https://doi.org/10.1142/s0218127419501220
  23. Yevseiev, S., Rzayev, K., Korol, O., Imanova, Z. (2016). Development of mceliece modified asymmetric crypto-code system on elliptic truncated codes. Eastern-European Journal of Enterprise Technologies, 4 (9 (82)), 18–26. https://doi.org/10.15587/1729-4061.2016.75250
  24. Yevseiev, S., Tsyhanenko, O., Ivanchenko, S., Aleksiyev, V., Verheles, D., Volkov, S. et al. (2018). Practical implementation of the Niederreiter modified crypto­code system on truncated elliptic codes. Eastern-European Journal of Enterprise Technologies, 6 (4 (96)), 24–31. https://doi.org/10.15587/1729-4061.2018.150903
  25. Yevseiev, S., Hryhorii, K., Liekariev, Y. (2016). Developing of multi-factor authentication method based on niederreiter-mceliece modified crypto-code system. Eastern-European Journal of Enterprise Technologies, 6 (4 (84)), 11–23. https://doi.org/10.15587/1729-4061.2016.86175
  26. Couvreur, A., Otmani, A., Tillich, J. (2014). Polynomial Time Attack on Wild McEliece over Quadratic Extensions. Advances in Cryptology – EUROCRYPT 2014, 17–39. https://doi.org/10.1007/978-3-642-55220-5_2
  27. Yevseiev, S., Korol, O., Kots, H. (2017). Construction of hybrid security systems based on the crypto-code structures and flawed codes. Eastern-European Journal of Enterprise Technologies, 4 (9 (88)), 4–21. https://doi.org/10.15587/1729-4061.2017.108461
  28. Yevseiev, S., Tsyhanenko, O., Gavrilova, A., Guzhva, V., Milov, O., Moskalenko, V. et al. (2019). Development of Niederreiter hybrid crypto-code structure on flawed codes. Eastern-European Journal of Enterprise Technologies, 1 (9 (97)), 27–38. https://doi.org/10.15587/1729-4061.2019.156620
  29. Zhang, G., Cai, S. (2017). Universal secure error-correcting (SEC) schemes for network coding via McEliece cryptosystem based on QC-LDPC codes. Cluster Computing, 22 (S2), 2599–2610. https://doi.org/10.1007/s10586-017-1354-x
  30. Baldi, M., Bianchi, M., Chiaraluce, F., Rosenthal, J., Schipani, D. (2014). Enhanced Public Key Security for the McEliece Cryptosystem. Journal of Cryptology, 29 (1), 1–27. https://doi.org/10.1007/s00145-014-9187-8
  31. Moufek, H., Guenda, K. (2017). A New variant of the McEliece cryptosystem based on the Smith form of convolutional codes. Cryptologia, 42 (3), 227–239. https://doi.org/10.1080/01611194.2017.1362061
  32. Dinh, H., Moore, C., Russell, A. (2011). McEliece and Niederreiter Cryptosystems That Resist Quantum Fourier Sampling Attacks. Advances in Cryptology – CRYPTO 2011, 761–779. https://doi.org/10.1007/978-3-642-22792-9_43
  33. Tsyhanenko, O., Rzayev, K., Mammadova, T. (2018). Mathematical model of the modified niederreiter crypto-code structures. Advanced Information Systems, 2 (4), 37–44. https://doi.org/10.20998/2522-9052.2018.4.06
  34. Massey, J. L. (1986). Theory and practice of error control codes. Proceedings of the IEEE, 74 (9), 1293–1294. https://doi.org/10.1109/proc.1986.13626
  35. Mishenko, V. A., Vilanskiy, Yu. V. (2007). Usherbnye teksty i mnogokanalnaya kriptografiya. Minsk: Enciklopediks.
  36. Mishenko, V. A., Vilanskiy, Yu. V., Lepin, V. V (2007). Kriptograficheskiy algoritm MV2. Minsk: Enciklopediks.
  37. Yevseiev, S. (2017). The use of damaged codes in crypto code systems. Systemy obrobky informatsiyi, 5, 109–121. Available at: http://nbuv.gov.ua/UJRN/soi_2017_5_17
  38. Voronin, A., Akhiiezer, O., Galuza, A., Lebedeva, I., Zaitsev, Y., Lebedev, S. (2023). Modeling Competitive Interaction “Predator-Prey” on the Example of Two Innovative Processes. 2023 13th International Conference on Advanced Computer Information Technologies (ACIT), 131–134. https://doi.org/10.1109/acit58437.2023.10275538
  39. Rukhin, A., Sota, J., Nechvatal, J., Smid, M., Barker, E., Leigh, S. et al. (2000). A statistical test suite for random and pseudorandom number generators for cryptographic applications. National Institute of Standards and Technology. NIST Special Publication 800-22. https://doi.org/10.6028/nist.sp.800-22
  40. Potіj, O. V. (2004). Metodika statistichnogo testuvannja NIST STS ta matematichne obґruntuvannja testіv. Tehnіchnij zvіt ІІT – 001-2004. Kharkiv, 62.
  41. Класифікатор кібербезпеки. Available at: https://skl.khpi.edu.ua/
  42. Shmatko, O., Balakireva, S., Vlasov, A., Zagorodna, N., Korol, O., Milov, O. et al. (2020). Development of methodological foundations for designing a classifier of threats to cyberphysical systems. Eastern-European Journal of Enterprise Technologies, 3 (9 (105)), 6–19. https://doi.org/10.15587/1729-4061.2020.205702
  43. Yevseiev, S., Khokhlachova, Yu., Ostapov, S., Laptiev, O., Korol, O., Milevskyi, S. et al.; Yevseiev, S., Khokhlachova, Yu., Ostapov, S., Laptiev, O. (Eds.) (2023). Models of socio-cyber-physical systems security. Kharkiv: РС ТЕСHNOLOGY СЕNTЕR, 184. https://doi.org/10.15587/978-617-7319-72-5
  44. Avinash, S. V. (2017). Understanding Activation Functions in Neural Networks. The Theory Of Everything. Available at: https://medium.com/the-theory-of-everything/understanding-activation- functions-in-neural-networks-9491262884e0
  45. AutoDraw. Available at: https://www.autodraw.com/
  46. Kreutz, D., Ramos, F. M. V., Esteves Verissimo, P., Esteve Rothenberg, C., Azodolmolky, S., Uhlig, S. (2015). Software-Defined Networking: A Comprehensive Survey. Proceedings of the IEEE, 103 (1), 14–76. https://doi.org/10.1109/jproc.2014.2371999
  47. Geetha, R., Thilagam, T. (2020). A Review on the Effectiveness of Machine Learning and Deep Learning Algorithms for Cyber Security. Archives of Computational Methods in Engineering, 28 (4), 2861–2879. https://doi.org/10.1007/s11831-020-09478-2
  48. Salvakkam, D. B., Saravanan, V., Jain, P. K., Pamula, R. (2023). Enhanced Quantum-Secure Ensemble Intrusion Detection Techniques for Cloud Based on Deep Learning. Cognitive Computation, 15 (5), 1593–1612. https://doi.org/10.1007/s12559-023-10139-2
  49. Tavallaee, M., Bagheri, E., Lu, W., Ghorbani, A. A. (2009). A detailed analysis of the KDD CUP 99 data set. 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, 1–6. https://doi.org/10.1109/cisda.2009.5356528
Розробка постквантових криптосистем на основі схеми Рао-Нама

##submission.downloads##

Опубліковано

2025-02-28

Як цитувати

Меленті, Є. О., Король, О. Г., Шульга, В. П., Мілевський, С. В., Сєвєрінов, О. В., Войтко, О. В., Rzayev, K., Гусарова, І. Г., Кравченко, С. О., & Pashayeva, S. (2025). Розробка постквантових криптосистем на основі схеми Рао-Нама. Eastern-European Journal of Enterprise Technologies, 1(9 (133), 35–48. https://doi.org/10.15587/1729-4061.2025.323195

Номер

Том 1 № 9 (133) (2025): Інформаційно-керуючі системи

Розділ

Інформаційно-керуючі системи

Ліцензія

Авторське право (c) 2025 Yevhen Melenti, Olha Korol, Volodymyr Shulha, Stanislav Milevskyi, Оleksandr Sievierinov, Oleksandr Voitko, Khazail Rzayev, Iryna Husarova, Serhii Kravchenko, Sevinj Pashayeva

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.