A technique for applying the symmetry method to solve a problem of torsional vibrations of disks of variable thickness
DOI:
https://doi.org/10.15587/1729-4061.2025.323561Keywords:
differential equation, disk of variable thickness, torsional vibrations, natural frequencies, method of symmetriesAbstract
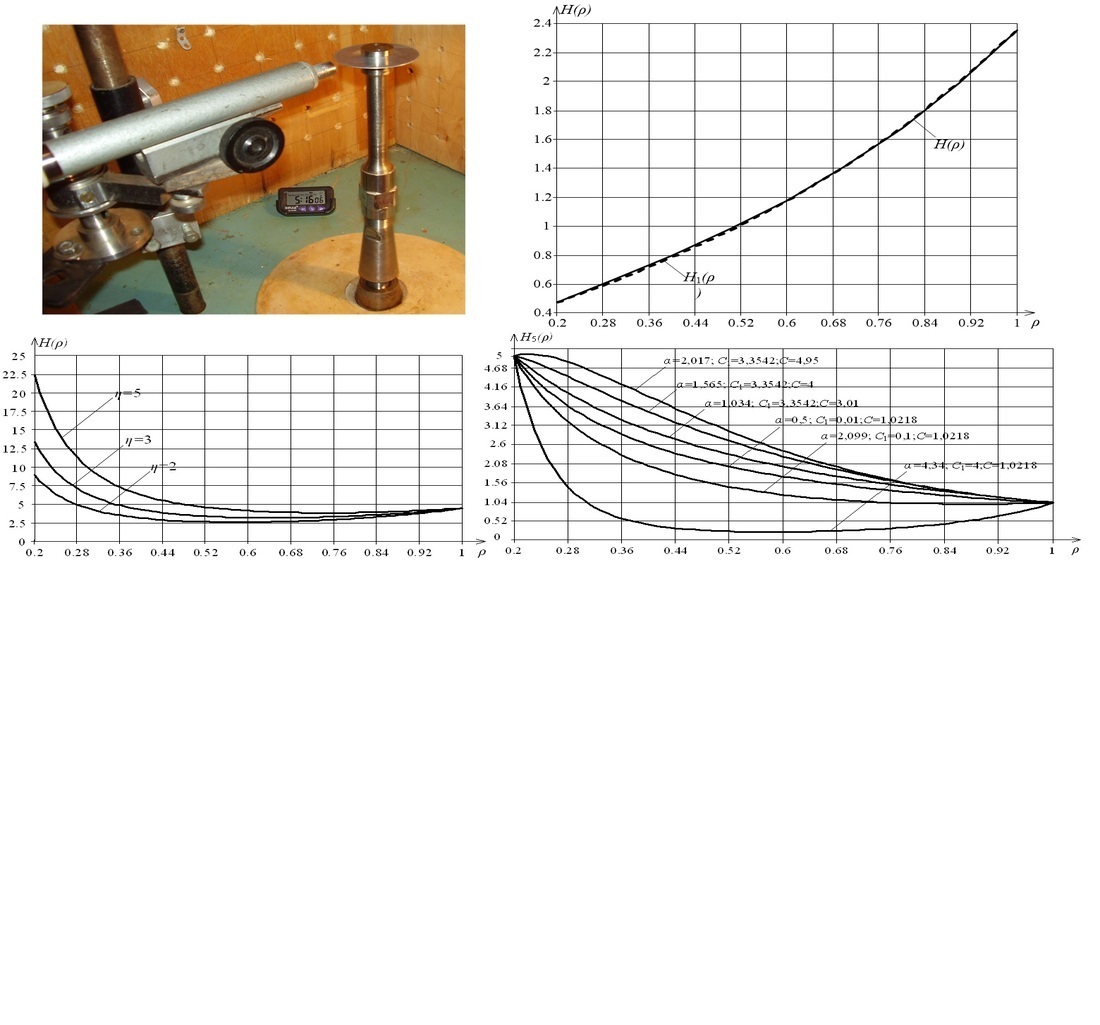
The object of this study is a disk of variable thickness. A solution to the problem of natural torsional vibrations of disks of variable thickness was sought. An algorithm to solve the problem for an arbitrary number of different disk profiles has been constructed. The law of change in disk thickness H(ρ), which contains three arbitrary constants α, С, С1, has been considered. The choice of the disk profile configuration is controlled by changing the values of these three constants.
Exact solutions to the problem in elementary functions are known only in two cases, when H(ρ)=1/ρ3 or H(ρ)=ρ-3eαρ, where ρ is the relative radial coordinate and α is an arbitrary constant. These cases are not sufficient for generalizing conclusions about the behavior of disks during their oscillations.
For the case of a disk that is rigidly fixed along its inner diameter and with a free outer edge, the corresponding relations were derived. They made it possible to calculate natural numbers and study the distribution of angular displacements of the disk. These numerical parameters, along with the frequency indices, are a convenient technique for evaluating the resonant properties of the disk for practice.
A comparison of torsional and radial vibrations of the disk with the chosen law of thickness change was performed. To study torsional vibrations, approximation approaches of thickness change functions were used. It was found that the relative discrepancy between the values of these functions at a certain interval did not exceed 2.2 %. It was found that the differences in the eigenfrequencies of torsional vibrations for the disk of the chosen configuration were significantly smaller than in the case of radial vibrations.
A practical algorithm for applying the method used is presented, which could prove useful for further research based on similar analytical approaches.
The method makes it possible to choose the desired disk configuration for various practical purposes. Owing to this feature, it is possible to provide the required distribution of cyclic stresses, resonant frequencies, and amplitudes for the disk
References
- Kumar, P., Tiwari, R. (2023). A review: multiplicative faults and model-based condition monitoring strategies for fault diagnosis in rotary machines. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 45 (5). https://doi.org/10.1007/s40430-023-04203-z
- Murawski, L., Dereszewski, M. (2019). Theoretical and practical backgrounds of monitoring system of ship power transmission systems’ torsional vibration. Journal of Marine Science and Technology, 25 (1), 272–284. https://doi.org/10.1007/s00773-019-00646-z
- Kim, Y. G., Kim, U. K. (2019). Effects of torsional vibration of a propulsion shafting system and energy efficiency design index from a system combining exhaust gas recirculation and turbocharger cut out. Journal of Mechanical Science and Technology, 33 (8), 3629–3639. https://doi.org/10.1007/s12206-019-0703-5
- Bai, B., Zhang, J., Cui, Y., Li, H. (2020). Vibration characteristics investigation of mistuned blisks with receptance substructure component modal synthesis method. Journal of Mechanical Science and Technology, 34 (7), 2715–2729. https://doi.org/10.1007/s12206-020-0604-7
- Kutsal, S. M., Coşkun, S. B. (2023). Analytical approximations for elastic limit angular velocities of rotating annular disks with hyperbolic thickness. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 45 (6). https://doi.org/10.1007/s40430-023-04132-x
- Salehian, M., Shahriari, B., Yousefi, M. (2018). Investigating the effect of angular acceleration of the rotating disk having variable thickness and density function on shear stress and tangential displacement. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 41 (1). https://doi.org/10.1007/s40430-018-1523-8
- Szuwalski, K., Ustrzycka, A. (2015). Mathematical and numerical modelling of large creep deformations for annular rotating disks. Applied Mathematics and Mechanics, 36 (11), 1441–1448. https://doi.org/10.1007/s10483-015-1994-7
- Bagheri, E., Asghari, M., Danesh, V. (2019). Analytical study of micro-rotating disks with angular acceleration on the basis of the strain gradient elasticity. Acta Mechanica, 230 (9), 3259–3278. https://doi.org/10.1007/s00707-019-02461-4
- Thakur, P., Sethi, M., Kumar, N., Gupta, K., Bhardwaj, R. K. (2021). Analytical Solution of Hyperbolic Deformable Disk having Variable Density. Mechanics of Solids, 56 (6), 1039–1046. https://doi.org/10.3103/s0025654421060194
- Bahrami Babamiri, B., Shahrjerdi, A., Bayat, M. (2020). Effect of geometrical imperfection on the thermomechanical behavior of functionally graded material rotating disk. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 42 (5). https://doi.org/10.1007/s40430-020-02360-z
- Biezeno, C. B., Grammel, R. (1939). Technische Dynamik. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-36257-0
- Trapezon, K., Trapezon, A., Kalinichenko, V., Didkovskii, V. (2024). Results of the analytical solution of the problem of radial vibrations of disks of variable thickness. Eastern-European Journal of Enterprise Technologies, 2 (7 (128)), 6–15. https://doi.org/10.15587/1729-4061.2024.300090
- Kamke, E. (1959). Differential gleichungen, Losungsmethoden und losungen. Leipzig, 244.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Kirill Trapezon, Alexandr Trapezon

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








