Спосіб застосування методу симетрії для розв’язання задачі про крутильні коливання дисків змінної товщини
DOI:
https://doi.org/10.15587/1729-4061.2025.323561Ключові слова:
диференціальне рівняння, диск змінної товщини, крутильні коливання, власні частоти, метод симетрійАнотація
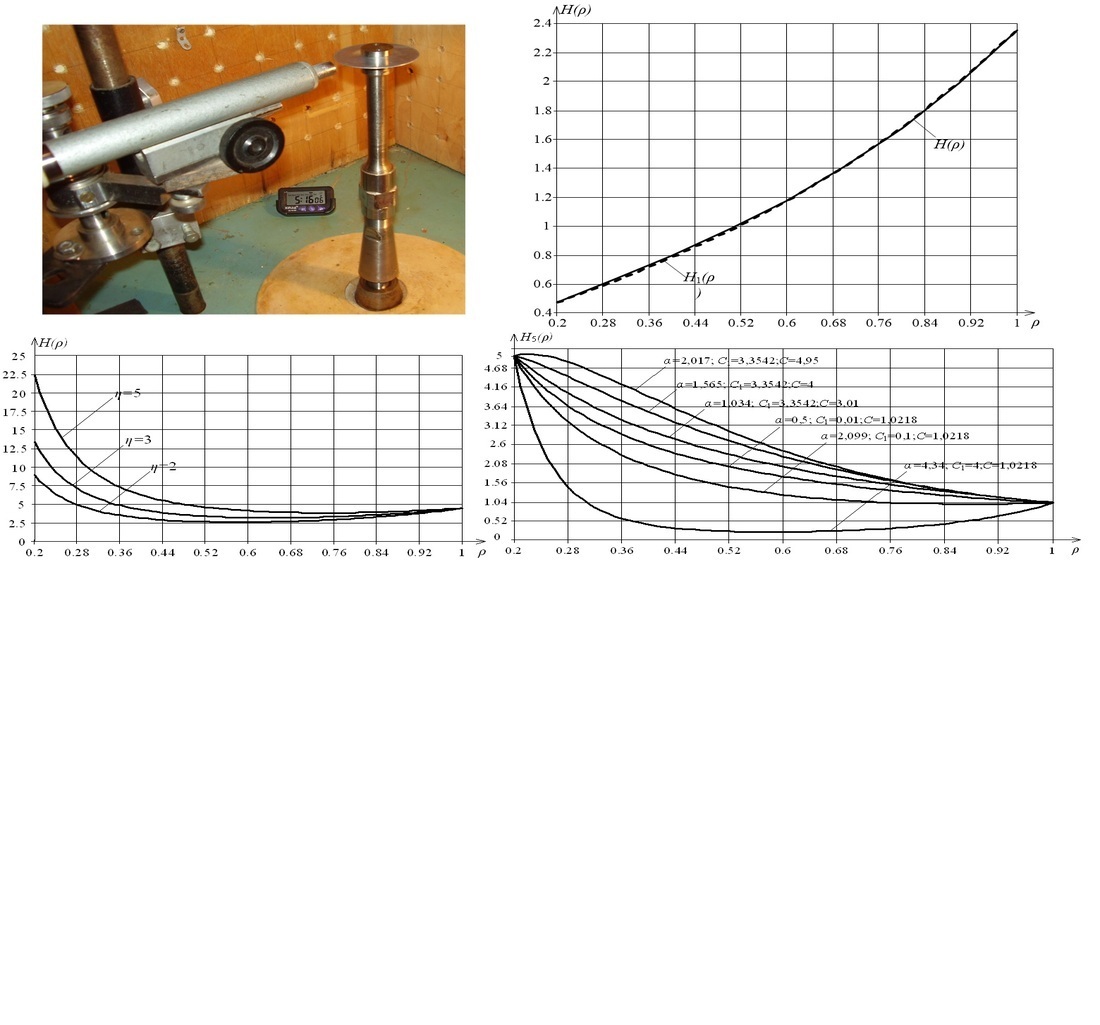
Об’єктом дослідження є диск змінної товщини. Розшукувався розв’язок задачі про власні крутильні коливання дисків змінної товщини. Побудовано алгоритм розв’язку задачі для довільної кількості різноманітних профілів диску. Розглянуто закон зміни товщини диска H(ρ), який містить у своєму складі три довільні сталі α,С,С1. Вибір конфігурації профілю диску контролюється шляхом зміни значень цих трьох сталих.
Відомі точні розв’язки задачі в елементарних функціях лише у двох випадках, коли H(ρ)=1/ ρ3 або H(ρ)= ρ-3eαρ, де ρ – відносна радіальна координата, α – довільна стала. Цих випадків не достатньо для узагальнюючих висновків про поведінку дисків при їх коливаннях.
Для випадку жорсткого закріплення диска по внутрішньому діаметру та з вільним зовнішнім краєм, отримано відповідні співвідношення. Вони дозволили обчислити власні числа, вивчити розподіл кутових переміщень диску. Наведені числові параметри, поряд з частотними показниками, є зручним засобом для оцінки резонансних властивостей диска для практики.
Проведено порівняння крутильних та радіальних коливань диску з обраним законом зміни товщини. Для вивчення крутильних коливань, використано підходи апроксимації функцій зміни товщини. Виявилось, що відносна розбіжність значень цих функцій на визначеному інтервалі не перевищує величини у 2,2 %. Отримано, що розходження власних частот крутильних коливань для диска обраної конфігурації суттєво менші, ніж у випадку радіальних коливань.
Наведено практичний алгоритм застосування використаного методу, який може бути корисний для подальших досліджень на основі подібних аналітичних підходів.
Метод дозволяє вибрати потрібну конфігурацією диска для різних практичних цілей. Завдяки такій можливості, можна забезпечити для диску необхідний розподіл циклічних напружень, резонансних частот та амплітуд
Посилання
- Kumar, P., Tiwari, R. (2023). A review: multiplicative faults and model-based condition monitoring strategies for fault diagnosis in rotary machines. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 45 (5). https://doi.org/10.1007/s40430-023-04203-z
- Murawski, L., Dereszewski, M. (2019). Theoretical and practical backgrounds of monitoring system of ship power transmission systems’ torsional vibration. Journal of Marine Science and Technology, 25 (1), 272–284. https://doi.org/10.1007/s00773-019-00646-z
- Kim, Y. G., Kim, U. K. (2019). Effects of torsional vibration of a propulsion shafting system and energy efficiency design index from a system combining exhaust gas recirculation and turbocharger cut out. Journal of Mechanical Science and Technology, 33 (8), 3629–3639. https://doi.org/10.1007/s12206-019-0703-5
- Bai, B., Zhang, J., Cui, Y., Li, H. (2020). Vibration characteristics investigation of mistuned blisks with receptance substructure component modal synthesis method. Journal of Mechanical Science and Technology, 34 (7), 2715–2729. https://doi.org/10.1007/s12206-020-0604-7
- Kutsal, S. M., Coşkun, S. B. (2023). Analytical approximations for elastic limit angular velocities of rotating annular disks with hyperbolic thickness. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 45 (6). https://doi.org/10.1007/s40430-023-04132-x
- Salehian, M., Shahriari, B., Yousefi, M. (2018). Investigating the effect of angular acceleration of the rotating disk having variable thickness and density function on shear stress and tangential displacement. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 41 (1). https://doi.org/10.1007/s40430-018-1523-8
- Szuwalski, K., Ustrzycka, A. (2015). Mathematical and numerical modelling of large creep deformations for annular rotating disks. Applied Mathematics and Mechanics, 36 (11), 1441–1448. https://doi.org/10.1007/s10483-015-1994-7
- Bagheri, E., Asghari, M., Danesh, V. (2019). Analytical study of micro-rotating disks with angular acceleration on the basis of the strain gradient elasticity. Acta Mechanica, 230 (9), 3259–3278. https://doi.org/10.1007/s00707-019-02461-4
- Thakur, P., Sethi, M., Kumar, N., Gupta, K., Bhardwaj, R. K. (2021). Analytical Solution of Hyperbolic Deformable Disk having Variable Density. Mechanics of Solids, 56 (6), 1039–1046. https://doi.org/10.3103/s0025654421060194
- Bahrami Babamiri, B., Shahrjerdi, A., Bayat, M. (2020). Effect of geometrical imperfection on the thermomechanical behavior of functionally graded material rotating disk. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 42 (5). https://doi.org/10.1007/s40430-020-02360-z
- Biezeno, C. B., Grammel, R. (1939). Technische Dynamik. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-36257-0
- Trapezon, K., Trapezon, A., Kalinichenko, V., Didkovskii, V. (2024). Results of the analytical solution of the problem of radial vibrations of disks of variable thickness. Eastern-European Journal of Enterprise Technologies, 2 (7 (128)), 6–15. https://doi.org/10.15587/1729-4061.2024.300090
- Kamke, E. (1959). Differential gleichungen, Losungsmethoden und losungen. Leipzig, 244.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2025 Kirill Trapezon, Alexandr Trapezon

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









