Creation of the generative model of a scale-free network with homophilic structure
DOI:
https://doi.org/10.15587/1729-4061.2025.326092Keywords:
scale-free property, homophily, modularity, generative network models, node communitiesAbstract
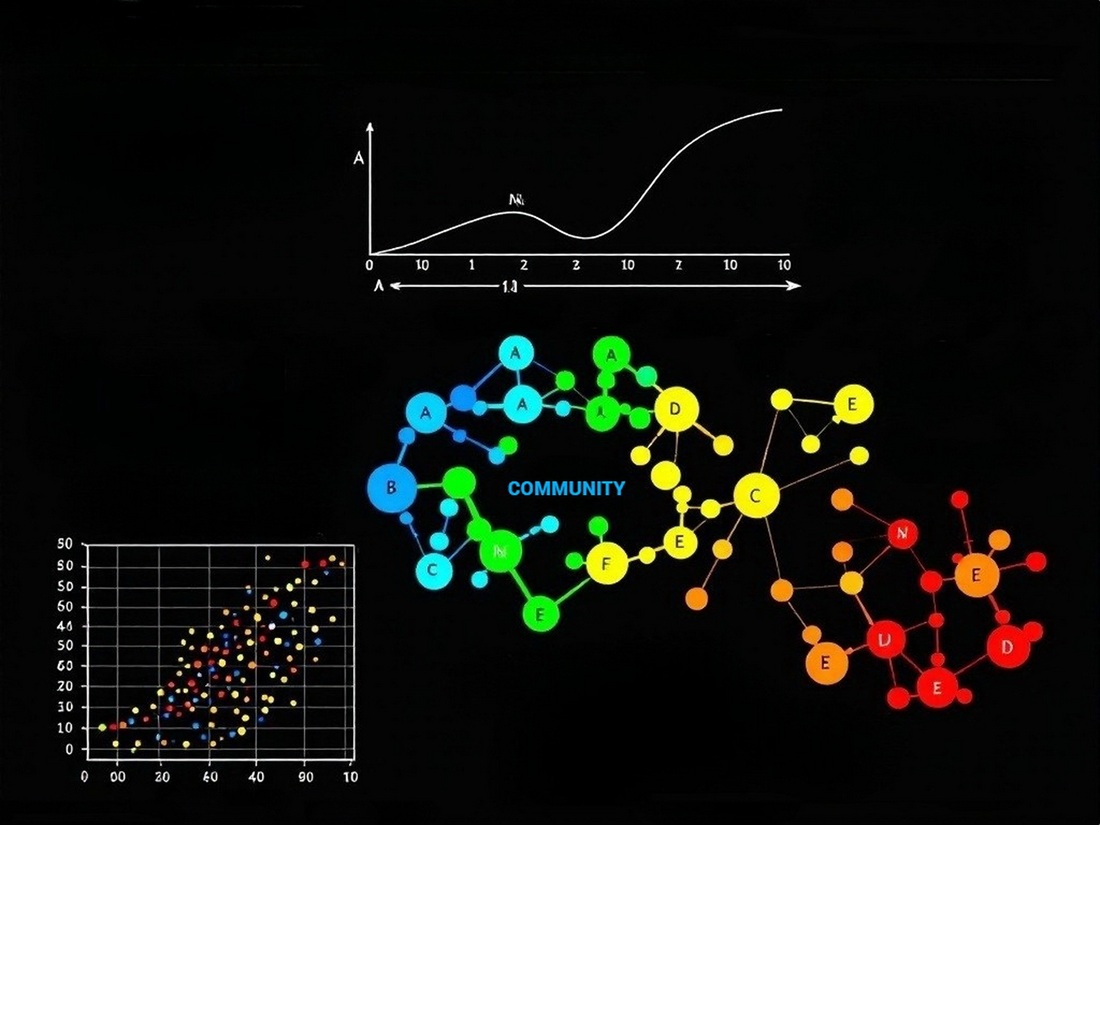
The object of this study is the models of complex networks. The task addressed is to construct a generative model of a growing network, which has two key features characteristic of real-world networks: scale-free property and homophily. Homophily of a network is understood as the tendency of nodes to group into communities. To combine the requirements for homophily and scale-free property, a two-level rule of preferential attachment has been devised. First, the color of a new node is chosen with a probability proportional to the volume of the corresponding community, and then, according to the usual rule of preferential attachment, neighboring nodes are chosen within the community. It has been shown that the computational complexity of generating a network model with n nodes is O(n). It has been proven that under such conditions, the distribution of degrees of nodes across the entire network is the same as in the classical non-homophilic Barabási-Albert network and does not depend on the number and structure of communities. Under the conditions of homophily, it is quite natural to generalize the requirement for scale-free property to the distribution of community sizes. It has been found that this distribution is determined by the intensity of the formation of new communities. The dependence of the expected time interval between the formations of successive communities on their index has been established. The measure of homophily of the generated networks – modularity – has been estimated; its dependence on the scaling of the community volumes was found. The model built allows step-by-step generation of growing scale-free networks that have a built-in mechanism for the formation of communities, which is of practical significance. Moreover, the proposed model could also be used in the opposite direction: given the structural parameters of the network, it is possible to restore the hidden rules by which this network evolves
References
- Li, A., Li, J., Pan, Y. (2013). Homophyly Networks – A Structural Theory of Networks. arXiv. https://doi.org/10.48550/arXiv.1310.8295
- Dorogovtsev, S. N., Mendes, J. F. F., Samukhin, A. N. (2000). Structure of Growing Networks with Preferential Linking. Physical Review Letters, 85 (21), 4633–4636. https://doi.org/10.1103/physrevlett.85.4633
- Newman, M. E. J. (2003). Mixing patterns in networks. Physical Review E, 67 (2). https://doi.org/10.1103/physreve.67.026126
- Mele, A. (2017). A Structural Model of Homophily and Clustering in Social Networks. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3031489
- Choromański, K., Matuszak, M., Miȩkisz, J. (2013). Scale-Free Graph with Preferential Attachment and Evolving Internal Vertex Structure. Journal of Statistical Physics, 151 (6), 1175–1183. https://doi.org/10.1007/s10955-013-0749-1
- Newman, M. (2005). Power laws, Pareto distributions and Zipf’s law. Contemporary Physics, 46 (5), 323–351. https://doi.org/10.1080/00107510500052444
- Albert, R., Barabási, A.-L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics, 74 (1), 47–97. https://doi.org/10.1103/revmodphys.74.47
- Noldus, R., Van Mieghem, P. (2015). Assortativity in complex networks. Journal of Complex Networks, 3 (4), 507–542. https://doi.org/10.1093/comnet/cnv005
- Shergin, V., Udovenko, S., Chala, L. (2020). Assortativity Properties of Barabási-Albert Networks. Data-Centric Business and Applications, 55–66. https://doi.org/10.1007/978-3-030-43070-2_4
- Li, A., Li, J., Pan, Y. (2013). Community Structures Are Definable in Networks, and Universal in Real World. arXiv. https://doi.org/10.48550/arXiv.1310.8294
- Girvan, M., Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99 (12), 7821–7826. https://doi.org/10.1073/pnas.122653799
- Shergin, V., Grinyov, S., Chala, L., Udovenko, S. (2024). Network community detection using modified modularity criterion. Eastern-European Journal of Enterprise Technologies, 6 (4 (132)), 6–13. https://doi.org/10.15587/1729-4061.2024.318452
- Shergin, V., Chala, L., Udovenko, S., Pogurskaya, M. (2020). Elastic Scale-Free Networks Model Based on the Mediaton-Driven Attachment Rule. 2020 IEEE Third International Conference on Data Stream Mining & Processing (DSMP), 291–295. https://doi.org/10.1109/dsmp47368.2020.9204207
- Raskin, L., Sira, O. (2021). Devising methods for planning a multifactorial multilevel experiment with high dimensionality. Eastern-European Journal of Enterprise Technologies, 5 (4 (113)), 64–72. https://doi.org/10.15587/1729-4061.2021.242304
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Vadim Shergin, Sergei Grinyov, Larysa Chala, Serhii Udovenko

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








