Розробка генеративної моделі безмасштабної мережі з гомофільною структурою
DOI:
https://doi.org/10.15587/1729-4061.2025.326092Ключові слова:
безмасштабність, гомофільність, модулярність, складні мережі, спільноти вузлівАнотація
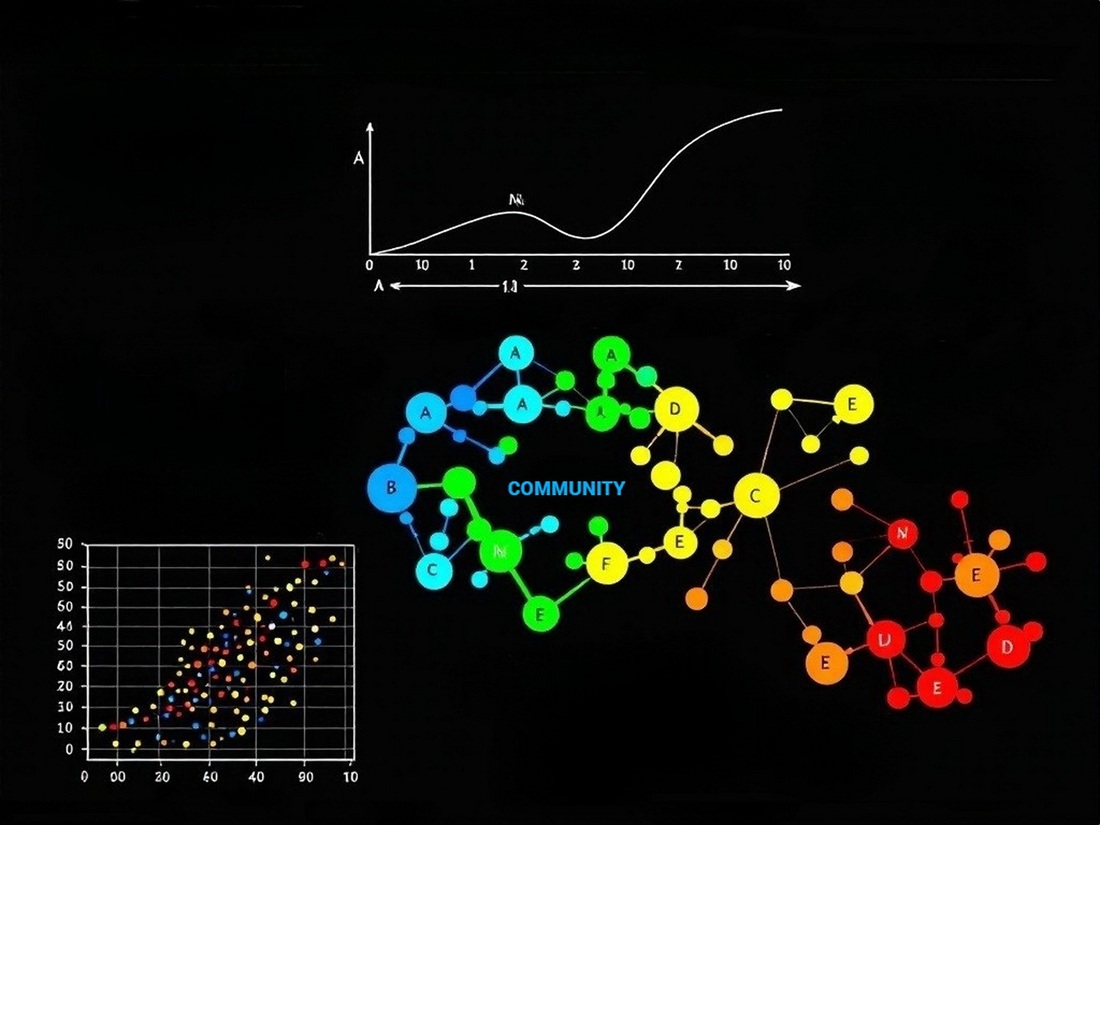
Об’єктом досліджень є моделі складних мереж. Розглядається проблема створення генеративної моделі зростаючої мережі, яка має дві ключові властивості, характерні для мереж реального світу: безмасштабність та гомофільність. Під гомофільністю мережі мається на увазі тяжіння вузлів до групування у спільноти. Для суміщення вимог щодо гомофільності та безмасштабності було розроблено дворівневе правило переважного приєднання вузла до мережі. Згідно з ним спочатку обирається колір нового вузла з ймовірністю, пропорційною до обсягу відповідної спільноти, а потім за звичайним правилом переважного приєднання серед спільноти обираються вузли-сусіди. Показано що обчислювальна складність генерації моделі мережі з n вузлів становить O(n). Доведено, що розподіл степенів вузлів всієї мережі є таким же, як у класичній негомофільній мережі Barabási-Albert та не залежить від кількості та структури спільнот. За умов гомофільності, цілком природнім є узагальнення вимоги щодо безмасштабності на розподіл розмірів та обсягів спільнот. Визначено, що зазначений розподіл визначається інтенсивністю утворення нових спільнот. Знайдено залежність очікуваного часового інтервалу між утворенням послідовних спільнот від поточної їх кількості, яка забезпечує безмасштабність розмірів спільнот з заданим показником скейлінгу. Оцінено міру гомофільності генерованих мереж – модулярність та визначено характер її залежності від скейлінгу обсягу спільнот. Створена модель дозволяє покроково генерувати зростаючі безмасштабні мережі, які мають вбудований механізм утворення спільнот, що має практичну значущість. Більше того, розроблена модель може бути використана й у зворотному напрямку: за заданими структурними параметрами мережі можна відновити приховані правила, за якими відбувається еволюція мережі
Посилання
- Li, A., Li, J., Pan, Y. (2013). Homophyly Networks – A Structural Theory of Networks. arXiv. https://doi.org/10.48550/arXiv.1310.8295
- Dorogovtsev, S. N., Mendes, J. F. F., Samukhin, A. N. (2000). Structure of Growing Networks with Preferential Linking. Physical Review Letters, 85 (21), 4633–4636. https://doi.org/10.1103/physrevlett.85.4633
- Newman, M. E. J. (2003). Mixing patterns in networks. Physical Review E, 67 (2). https://doi.org/10.1103/physreve.67.026126
- Mele, A. (2017). A Structural Model of Homophily and Clustering in Social Networks. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3031489
- Choromański, K., Matuszak, M., Miȩkisz, J. (2013). Scale-Free Graph with Preferential Attachment and Evolving Internal Vertex Structure. Journal of Statistical Physics, 151 (6), 1175–1183. https://doi.org/10.1007/s10955-013-0749-1
- Newman, M. (2005). Power laws, Pareto distributions and Zipf’s law. Contemporary Physics, 46 (5), 323–351. https://doi.org/10.1080/00107510500052444
- Albert, R., Barabási, A.-L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics, 74 (1), 47–97. https://doi.org/10.1103/revmodphys.74.47
- Noldus, R., Van Mieghem, P. (2015). Assortativity in complex networks. Journal of Complex Networks, 3 (4), 507–542. https://doi.org/10.1093/comnet/cnv005
- Shergin, V., Udovenko, S., Chala, L. (2020). Assortativity Properties of Barabási-Albert Networks. Data-Centric Business and Applications, 55–66. https://doi.org/10.1007/978-3-030-43070-2_4
- Li, A., Li, J., Pan, Y. (2013). Community Structures Are Definable in Networks, and Universal in Real World. arXiv. https://doi.org/10.48550/arXiv.1310.8294
- Girvan, M., Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99 (12), 7821–7826. https://doi.org/10.1073/pnas.122653799
- Shergin, V., Grinyov, S., Chala, L., Udovenko, S. (2024). Network community detection using modified modularity criterion. Eastern-European Journal of Enterprise Technologies, 6 (4 (132)), 6–13. https://doi.org/10.15587/1729-4061.2024.318452
- Shergin, V., Chala, L., Udovenko, S., Pogurskaya, M. (2020). Elastic Scale-Free Networks Model Based on the Mediaton-Driven Attachment Rule. 2020 IEEE Third International Conference on Data Stream Mining & Processing (DSMP), 291–295. https://doi.org/10.1109/dsmp47368.2020.9204207
- Raskin, L., Sira, O. (2021). Devising methods for planning a multifactorial multilevel experiment with high dimensionality. Eastern-European Journal of Enterprise Technologies, 5 (4 (113)), 64–72. https://doi.org/10.15587/1729-4061.2021.242304
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2025 Vadim Shergin, Sergei Grinyov, Larysa Chala, Serhii Udovenko

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.










