Development of a procedure for calculating problems in the mechanics of elastomers based on the open modeling language

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.326219

Keywords:

moment finite element scheme, variational principle of Lagrange, mathematical model of elastomeric structures

Abstract

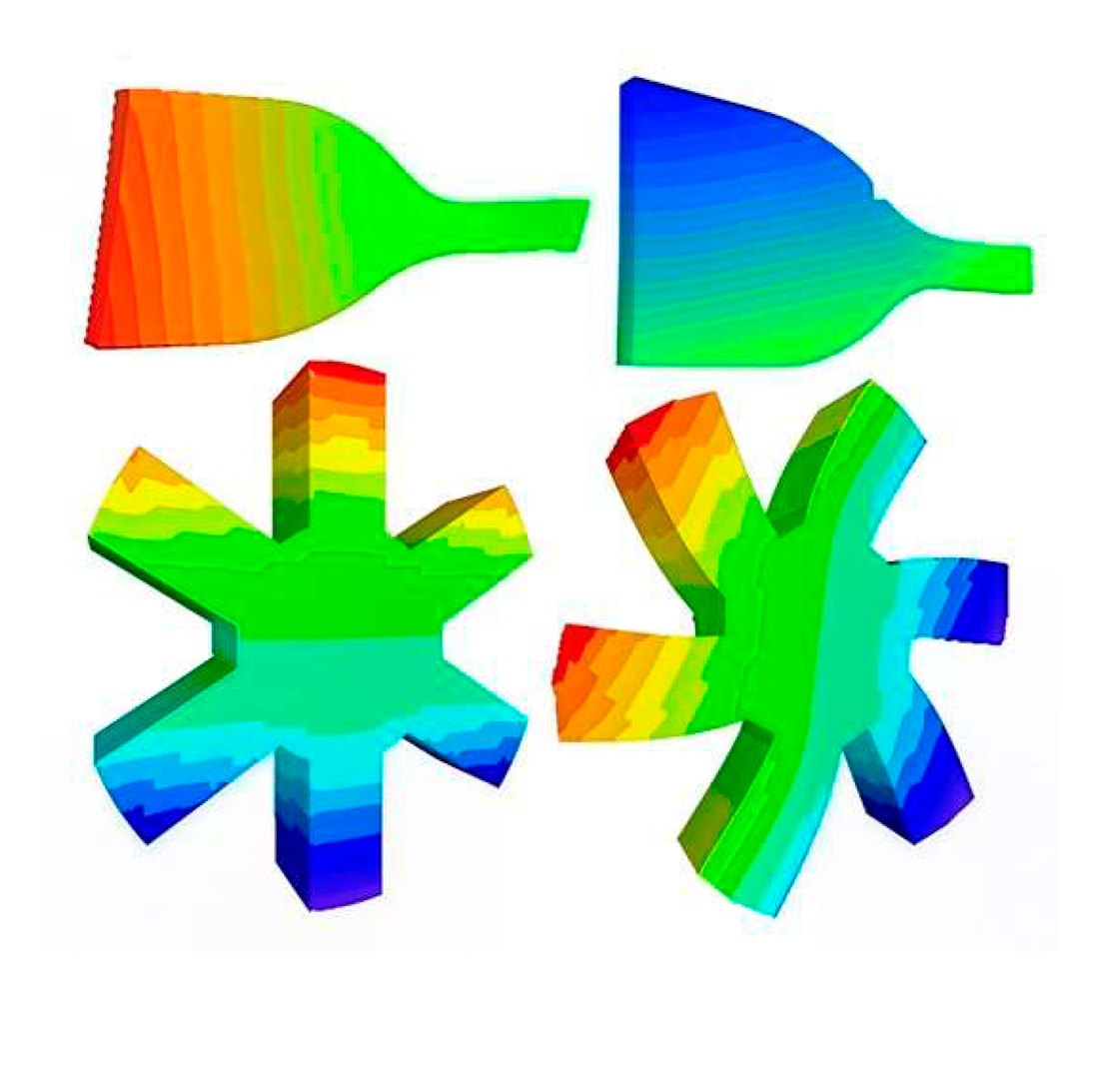
The object of the study is the stress-strain state of elastomeric structures. When solving practical problems in elastomer mechanics, the issue of selecting an effective computational scheme based on computational mathematics methods arises. However, due to the insufficient number of studies, it is difficult to assess the optimality of a particular methodology, which necessitates an analysis of computational algorithms followed by a comparison of their advantages and disadvantages.

In the design of elastomeric structures, the numerical analysis of their stress-strain state is a relevant issue. One of the key characteristics is the compressibility of the material, which is not taken into account by equations for incompressible media. In thin-layer rubber elements, this effect becomes more pronounced as the ratio of one of the geometric dimensions to the thickness of the structure increases.

The use of the finite element method in displacements, despite its convenience, encounters computational errors. When the Poisson's ratio approaches 0.5, numerical instabilities arise, complicating the attainment of reliable computational results.

This study proposes a new approach to organizing computational schemes in specialized automated design systems, which ensures more accurate modeling of the stress-strain state of structures. The foundation is the use of Open Modeling Language, which simplifies the description of mechanics problems and corresponding numerical schemes within a unified variational framework.

The key result is the derivation of universal formulas for determining the potential energy of the system based on the moment finite element scheme. The proposed approach eliminates the “false shear” effect and improves the accuracy of numerical calculations for weakly compressible materials, which is confirmed by numerical analysis and experimental data

Author Biographies

Volodymyr Lavrik, Kyiv National University of Technologies and Design

PhD

Department of Information and Computer Technologies

Ihor Bohdanov, Berdyansk State Pedagogical University

Doctor of Pedagogical Sciences, Professor, Corresponding Member of the National Academy of Educational Sciences of Ukraine, Honored Worker of Science and Technology of Ukraine

Rector

Department of Professional Education, Labor Training and Technologies

Hanna Alieksieieva, Berdyansk State Pedagogical University

PhD, Associate Professor

Department of Computer Technologies and Computer Science

Oleksandr Antonenko, Berdyansk State Pedagogical University

PhD, Associate Professor

Department of Computer Technologies and Computer Science

Oleksandr Ovsyannikov, Berdyansk State Pedagogical University

PhD, Associate Professor

Department of Computer Technologies and Computer Science

References

  1. Biderman, V. L., Sukhova, N. A. (1968). Calculation of cylindrical and rectangular long rubber compression shock absorbers. Strength of Materials, 13, 55–72.
  2. Bulat, A. F., Dirda, V. I., Karnaukhov, V. G., Agal’tsov, G. M. (2021). Effect of Ionizing Radiation on the Mechanical Behavior of Rubber Materials. International Applied Mechanics, 57 (4), 379–385. https://doi.org/10.1007/s10778-021-01089-z
  3. Drass, M. (2020). Elastomers and their Mechanical Behaviour. Constitutive Modelling and Failure Prediction for Silicone Adhesives in Façade Design, 37–63. https://doi.org/10.1007/978-3-658-29255-3_3
  4. Feng, H., Zhou, J., Gao, S., Jiang, L. (2021). Finite element simulation of the viscoelastic behavior of elastomers under finite deformation with consideration of nonlinear material viscosity. Acta Mechanica, 232 (10), 4111–4132. https://doi.org/10.1007/s00707-021-03042-0
  5. Grebenyuk, S., Smoliankova, T., Klymenko, M., Kudin, O. (2020). The homogenization of multi­modular composites at their longitudinal deformation. Eastern-European Journal of Enterprise Technologies, 3 (7 (105)), 13–19. https://doi.org/10.15587/1729-4061.2020.199968
  6. Zhang, L., Yu, W. (2015). Variational asymptotic homogenization of elastoplastic composites. Composite Structures, 133, 947–958. https://doi.org/10.1016/j.compstruct.2015.07.117
  7. Martynenko, V. G., L'vov, G. I. (2016). A numerical method for determining anisotropic visco-elastic properties of orthogonally reinforced composite material. Vestnik NTU "KhPI". Series: Dynamics and Strength of Machines, 46 (1218), 44–51.
  8. Nikishkov, G., Nikishkov, Y., Makeev, A. (2013). Finite element mesh generation for composites with ply waviness based on X-ray computed tomography. Advances in Engineering Software, 58, 35–44. https://doi.org/10.1016/j.advengsoft.2013.01.002
  9. Dyrda, V., Lapin, V., Lysytsia, M., Puhach, A., Bulat, I., Pankevych, I. et al. (2022). Some problems of the new radiation-resistant rubber mechanics in vibrating machines at hard γ-radiation. IOP Conference Series: Earth and Environmental Science, 970 (1), 012017. https://doi.org/10.1088/1755-1315/970/1/012017
  10. Mezhuyev, V., Lavrik, V. (2015). Improved Finite Element Approach for Modeling Three-Dimensional Linear-Elastic Bodies. Indian Journal of Science and Technology, 8 (30). https://doi.org/10.17485/ijst/2015/v8i1/57727
  11. Bulat, À. F., Dyrda, V. I., Grebenyuk, S. M., Klymenko, M. I. (2020). Determination of Effective Characteristics of a Fibrous Composite with Account of Viscoelastic Deformation of its Components. Strength of Materials, 52 (5), 691–699. https://doi.org/10.1007/s11223-020-00221-7
  12. Gulyar, A. I., Sakharov, A. S., Stepashko, V. I. (1986). Application of the semianalytical finite element method to solving spatial problems of fracture mechanics of axisymmetric bodies. Strength of Materials, 18 (7), 959–963. https://doi.org/10.1007/bf01522700
  13. Bulat, A. F., Dyrda, V. I., Grebenyuk, S. M., Klymenko, M. I. (2022). Numerical Simulation of Viscoelastic Deformation of Rubber Shock Absorbers Based on the Exponential Law. Strength of Materials, 54 (5), 776–784. https://doi.org/10.1007/s11223-022-00454-8
  14. Çakmak, U. D., Major, Z. (2013). Experimental Thermomechanical Analysis of Elastomers Under Uni- and Biaxial Tensile Stress State. Experimental Mechanics, 54 (4), 653–663. https://doi.org/10.1007/s11340-013-9820-8
  15. Choporov, S., Homeniuk, S., Grebenyuk, S. (2018). Optimized smoothing of discrete models of the implicitly defined geometrical objects’ surfaces. Eastern-European Journal of Enterprise Technologies, 3 (4 (93)), 52–60. https://doi.org/10.15587/1729-4061.2018.130787
  16. Re, D., De Angelis, F., Augusti, G., Augusti, D., Caputi, S., D’Amario, M., D’Arcangelo, C. (2015). Mechanical Properties of Elastomeric Impression Materials: An In Vitro Comparison. International Journal of Dentistry, 2015, 1–8. https://doi.org/10.1155/2015/428286
  17. Rocker, S., Rayer, M., Ternes, S., Schiffers, R. (2023). Substitution of elastomer components under cyclic loading by thermoplastic elastomers: Investigations of static and dynamic properties. Structural And Physical Aspects Of Construction Engineering 2022 (SPACE 2022): 5th International Scientific Conference, 2950, 150002. https://doi.org/10.1063/5.0168347
  18. Menning, J. D. M., Ewert, A., Prokopchuk, A., Schlecht, B., Henke, M., Wallmersperger, T. (2023). Finite element based modeling and simulation of an elastomer gear rim. PAMM, 23 (1). https://doi.org/10.1002/pamm.202200141
  19. Piszko, P., Kryszak, B., Gazińska, M., Słota, D., Sobczak-Kupiec, A., Włodarczyk, M. et al. (2023). The effect of filler content on mechanical properties and cell response of elastomeric PGS/apatite foam scaffolds. Ceramics International, 49 (15), 25353–25363. https://doi.org/10.1016/j.ceramint.2023.05.071
  20. Borreguero, A. M., Izarra, I., Garrido, I., Trzebiatowska, P. J., Datta, J., Serrano, Á. et al. (2021). Thermal and Mechanical Behavior of Elastomers Incorporated with Thermoregulating Microcapsules. Applied Sciences, 11 (12), 5370. https://doi.org/10.3390/app11125370
  21. Mezhuyev, V., Homenyuk, S., Lavrik, V. (2015). Computation of elastomers properties using FORTU-FEM CAD system. ARPN Journal of Engineering and Applied Sciences, 10 (20), 9167–9173. Available at: https://www.arpnjournals.org/jeas/research_papers/rp_2015/jeas_1115_2853.pdf
  22. Coll, N., Guerrieri, M. (2017). Parallel constrained Delaunay triangulation on the GPU. International Journal of Geographical Information Science, 31 (7), 1467–1484. https://doi.org/10.1080/13658816.2017.1300804
  23. Fayolle, P.-A., Pasko, A. (2012). Optimized surface discretization of functionally defined multi-material objects. Advances in Engineering Software, 45 (1), 301–312. https://doi.org/10.1016/j.advengsoft.2011.10.007
  24. Choporov, S., Homeniuk, S., Grebenyuk, S., Kudin, O. (2019). Development of a method for triangulation of inhomogeneous regions represented by functions. Eastern-European Journal of Enterprise Technologies, 4 (4 (100)), 21–27. https://doi.org/10.15587/1729-4061.2019.174010
  25. Hniezdovskyi, O., Kudin, O., Belokon, Y., Kruglyak, D., Ilin, S. (2022). Designing an object-oriented architecture for the finite element simulation of structural elements. Eastern-European Journal of Enterprise Technologies, 6 (2 (120)), 78–84. https://doi.org/10.15587/1729-4061.2022.268018
  26. Havrylenko, Y., Cortez, J. I., Kholodniak, Y., Alieksieieva, H., Garcia, G. T. (2020). Modelling of Surfaces of Engineering Products on the Basis of Array of Points. Tehnicki Vjesnik, 27(6), 2034–2043. https://doi.org/10.17559/tv-20190720081227
  27. Marinkovic, D., Zehn, M. (2019). Survey of Finite Element Method-Based Real-Time Simulations. Applied Sciences, 9 (14), 2775. https://doi.org/10.3390/app9142775
  28. Hayeemasae, N., Soontaranon, S., Rasidi, M. S. M., Masa, A. (2021). Tensile and structural properties of natural rubber vulcanizates with different mastication times. Polímeros, 31 (1). https://doi.org/10.1590/0104-1428.09120
  29. Humova zirochka vid vyrobnyka. Ukrpromservis. Available at: https://zavod-rti.com/gumova-zirochka-vid-virobnika/
Development of a procedure for calculating problems in the mechanics of elastomers based on the open modeling language

Downloads

Published

2025-04-29

How to Cite

Lavrik, V., Bohdanov, I., Alieksieieva, H., Antonenko, O., & Ovsyannikov, O. (2025). Development of a procedure for calculating problems in the mechanics of elastomers based on the open modeling language. Eastern-European Journal of Enterprise Technologies, 2(7 (134), 23–32. https://doi.org/10.15587/1729-4061.2025.326219

Issue

Vol. 2 No. 7 (134) (2025): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2025 Volodymyr Lavrik, Ihor Bohdanov, Hanna Alieksieieva, Oleksandr Antonenko, Oleksandr Ovsyannikov

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.