Development of an algorithm for analytical modeling of the dynamics of random processes in an asymmetric Markov chain

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.327111

Keywords:

reliability of systems, Markov process, Kolmogorov equation, state probabilities, autonomous subsystems

Abstract

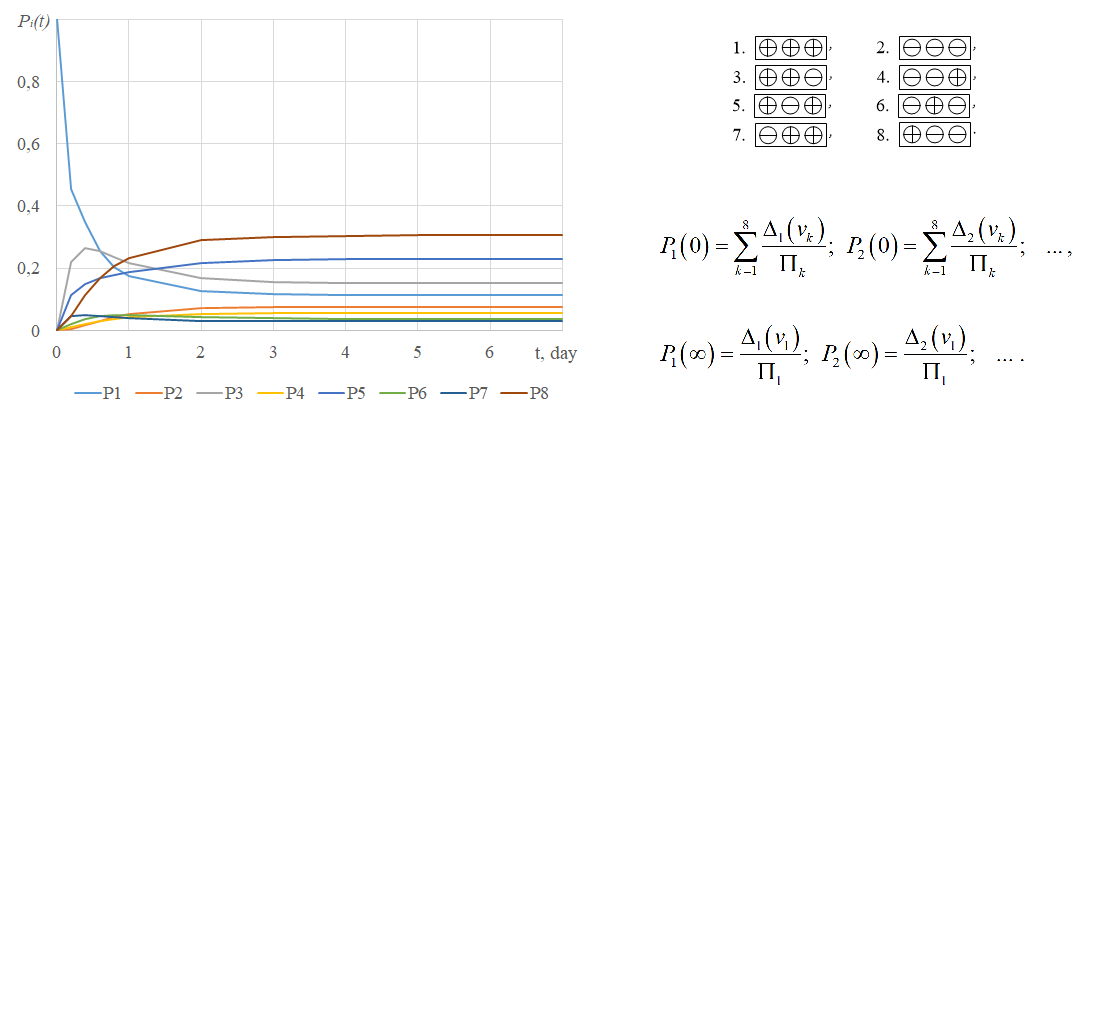
The object of this study is the reliability of a military structure consisting of three separate autonomous units. The task to develop an algorithm has been solved by taking into account the exact analytical solution to Kolmogorov’s differential equations, derived from the concept of harmonization of the mathematical description of models. The result of mathematical description harmonization manifests itself in the asymmetric structure of possible states of the system under study, consisting of three autonomous subsystems. The symmetric distribution of roots in the characteristic Kolmogorov equation on the complex plane in the ordered record of matrix tables and corresponding determinant tables has been revealed. The representation of the expanded formulas in the form of ordered tables makes it possible to adapt the algorithm to computer technologies and reduce computational costs by 2–3 times compared to conventional methods of numerical integration.

The results were verified by testing the algorithm on the example of assessing the reliability of a military structure consisting of three separate autonomous units. The probabilities of possible states of the military structure were determined depending on the intensity of the flow of losses and the restoration of combat units. The derived abstract, dimensionless results regarding the probabilities of states were interpreted through the physically significant time factor of the combat-ready state of combat units and the military structure as a whole. The results of calculations, as well as the algorithm and the mathematical model, have been validated by using a time-invariant condition that relates the probability of the system’s states

Author Biographies

Victor Kravets, Dnipro University of Technology

Doctor of Technical Sciences, Professor

Department of Automobiles and Automobile Economy

Valerii Domanskyi, O. M. Beketov National University of Urban Economy in Kharkiv

Doctor of Technical Sciences, Professor

Department of Electric Transport

Illia Domanskyi, Ukrainian State University of Science and Technologies

Doctor of Technical Sciences, Associate Professor

Department of Power Engineering

Volodymyr Kravets, Ivano-Frankivsk Professional College of Lviv National Environmental University

PhD, Associate Professor

Department of Horticulture and Park Management

References

  1. Igdalov, I. M., Kuchma, L. D., Polyakov, N. V., Sheptun, Yu. D. (2010). Dinamicheskoe proektirovanie raket. Zadachi dinamiki raket i ih kosmicheskih stupeney. Dnipro: Izd-vo Dnepropetr. nac. un-ta, 264.
  2. Kravets, V. V., Bass, K., Kravets, T., Tokar, L. (2015). Dynamic Design of Ground Transport With the Help of Computational Experiment. Mechanics, Materials Science & Engineering Journal. Available at: https://hal.science/hal-01305939/
  3. Hajek, B. (2015). Random Processes for Engineers. Cambridge University Press, 448. Available at: https://hajek.ece.illinois.edu/Papers/randomprocJuly14.pdf
  4. Domanskyi, V., Domanskyi, I., Zakurdai, S., Liubarskyi, D. (2022). Development of technologies for selecting energy-efficient power supply circuits of railway traction networks. Technology Audit and Production Reserves, 4 (1 (66)), 47–54. https://doi.org/10.15587/2706-5448.2022.263961
  5. Glushkov, V. M. (1980). Fundamental'nye issledovaniya i tehnologiya programmirovaniya. Programmirovanie, 2, 3–13.
  6. Andrews, J. G., McLone, R. R. (1976). Mathematical Modelling. Butterworths, 260.
  7. Van Tassel, D. (1978). Program Style, Design, Efficiency, Debugging, and Testing. Prentice Hall.
  8. Ovchynnykov, P. P. (Ed.) (2004). Vyshcha matematyka. Ch. 2. Kyiv, 792.
  9. Alpatov, A., Kravets, V., Kravets, V., Lapkhanov, E. (2021). Analytical modeling of the binary dynamic circuit motion. Transactions on Engineering and Computing Sciences, 9 (5), 23–32. https://doi.org/10.14738/tmlai.95.10922
  10. Kravets, V. V., Kapitsa, M. I., Domanskyi, I. V., Kravets, V. V., Hryshechkina, T. S., Zakurday, S. O. et al. (2024). Analytical Solution of Kolmogorov Equations for Asymmetric Markov Chains with Four and Eight States. Mathematics and Computer Science: Contemporary Developments Vol. 10, 140–162. https://doi.org/10.9734/bpi/mcscd/v10/3410
  11. Pender, J. (2014). Nonstationary loss queues via cumulant moment approximations. Probability in the Engineering and Informational Sciences, 29 (1), 27–49. https://doi.org/10.1017/s0269964814000205
  12. Sadeghian, P., Han, M., Håkansson, J., Zhao, M. X. (2024). Testing feasibility of using a hidden Markov model on predicting human mobility based on GPS tracking data. Transportmetrica B: Transport Dynamics, 12 (1). https://doi.org/10.1080/21680566.2024.2336037
  13. Seabrook, E., Wiskott, L. (2023). A Tutorial on the Spectral Theory of Markov Chains. Neural Computation, 35 (11), 1713–1796. https://doi.org/10.1162/neco_a_01611
  14. Chen, X., Li, L., Shi, Q. (2015). Stochastic Evolutions of Dynamic Traffic Flow. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-44572-3 3
  15. Kravets, V., Kravets, V., Burov, O. (2016). Reliability of Systems. Part 2. Dynamics of Failures. Saarbrucken: LAP LAMBERT Academic Publishing, 108.
  16. Kravets, V. V., Bass, K. M., Kravets, V. V., Tokar, L. A. (2014). Analytical Solution of Kolmogorov Equations for Four-Condition Homogenous, Symmetric and Ergodic System. Open Journal of Applied Sciences, 04 (10), 497–500. https://doi.org/10.4236/ojapps.2014.410048
  17. Kravets, V., Kravets, V., Burov, O. (2021). Analytical Modeling of the Dynamic System of the Fourth Order. Transactions on Machine Learning and Artificial Intelligence, 9 (3), 14–24. https://doi.org/10.14738/tmlai.93.9947
  18. Kravets, V., Kapitsa, M., Domanskyi, I., Kravets, V., Hryshechkina, T., Zakurday, S. (2024). Devising an analytical method for solving the eighth-order Kolmogorov equations for an asymmetric Markov chain. Eastern-European Journal of Enterprise Technologies, 5 (4 (131)), 33–41. https://doi.org/10.15587/1729-4061.2024.312971
  19. Kravets, V., Chibushov, Y. (1994). Method of Finding the Analytical Solution of the Algebraic Particular Aspect Equation. Rzeszow, 104–117.
  20. Domanskyi, I. V. (2016). Osnovy enerhoefektyvnosti elektrychnykh system z tiahovymy navantazhenniamy. Kharkiv: TOV «Tsentr informatsiyi transportu Ukrainy», 224. Available at: http://library.kpi.kharkov.ua/files/new_postupleniya/oceesi.pdf
  21. Bellman, R. (1997). Introduction to Matrix Analysis. SIAM. https://doi.org/10.1137/1.9781611971170
  22. Sigorskiy, V. P. (1977). Matematicheskiy apparat inzhenera. Kyiv: Tehnika.
  23. Ayyub, B., Mecuen, R. (1997). Probability, statistics & reliability for engineers. CRC Press, 663.
  24. Korn, G., Korn, T. (1984). Spravochnik po matematike dlya nauchnyh rabotnikov i inzhenerov. Moscow: Nauka.
  25. Vencel', E. S., Ovcharov, L. A. (2000). Teoriya sluchaynyh processov i ee inzhenernye prilozheniya. Moscow, 383.
  26. Blehman, I. I., Myshkis, A. D., Panovko, Ya. G. (1983). Mehanika i prikladnaya matematika. Logika i osobennosti prilozheniya matematiki. Moscow: Nauka, 328.
  27. Asmussen, S. (2008). Applied Probability and Queues. Springer Science & Business Media, 438. https://doi.org/10.1007/b97236
  28. Yun, M., Qin, W., Yang, X., Liang, F. (2019). Estimation of urban route travel time distribution using Markov chains and pair-copula construction. Transportmetrica B: Transport Dynamics, 7 (1), 1521–1552. https://doi.org/10.1080/21680566.2019.1637798
  29. Suliankatchi Abdulkader, R., Deneshkumar, V., Senthamarai Kannan, K., Koyilil, V., Paes, A. T., Sebastian, T. (2021). An application of Markov chain modeling and semi-parametric regression for recurrent events in health data. Communications in Statistics: Case Studies, Data Analysis and Applications, 8 (1), 68–80. https://doi.org/10.1080/23737484.2021.1973926
  30. Ray, S. N., Bose, S., Chattopadhyay, S. (2020). A Markov chain approach to the predictability of surface temperature over the northeastern part of India. Theoretical and Applied Climatology, 143 (1-2), 861–868. https://doi.org/10.1007/s00704-020-03458-z
  31. Wigner, E. P. (1979). Symmetries and Reflections: Scientific Essays. Ox Bow Press, 280.
  32. Elliott, J. P., Dawber, P. G. (1985). Symmetry in physics: Principles and Simple Applications. Vol. 1. Oxford University Press.
  33. Myamlin, S. V., Kravec, V. V. (2003). Simmetriya matematicheskoy modeli i dostovernost' vychislitel'nogo eksperimenta. Zbirnyk naukovykh prats Vinnytskoho derzhavnoho ahrarnoho universytetu, 15, 339–340.
Development of an algorithm for analytical modeling of the dynamics of random processes in an asymmetric Markov chain

Downloads

Published

2025-04-30

How to Cite

Kravets, V., Domanskyi, V., Domanskyi, I., & Kravets, V. (2025). Development of an algorithm for analytical modeling of the dynamics of random processes in an asymmetric Markov chain. Eastern-European Journal of Enterprise Technologies, 2(4 (134), 32–46. https://doi.org/10.15587/1729-4061.2025.327111

Issue

Vol. 2 No. 4 (134) (2025): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2025 Victor Kravets, Valerii Domanskyi, Illia Domanskyi, Volodymyr Kravets

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.