Development of a local density optimization approach for structure improvement and cluster separation in water quality data

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.337049

Keywords:

water quality, unsupervised clustering, density transformation, principal component analysis, Pasca distance

Abstract

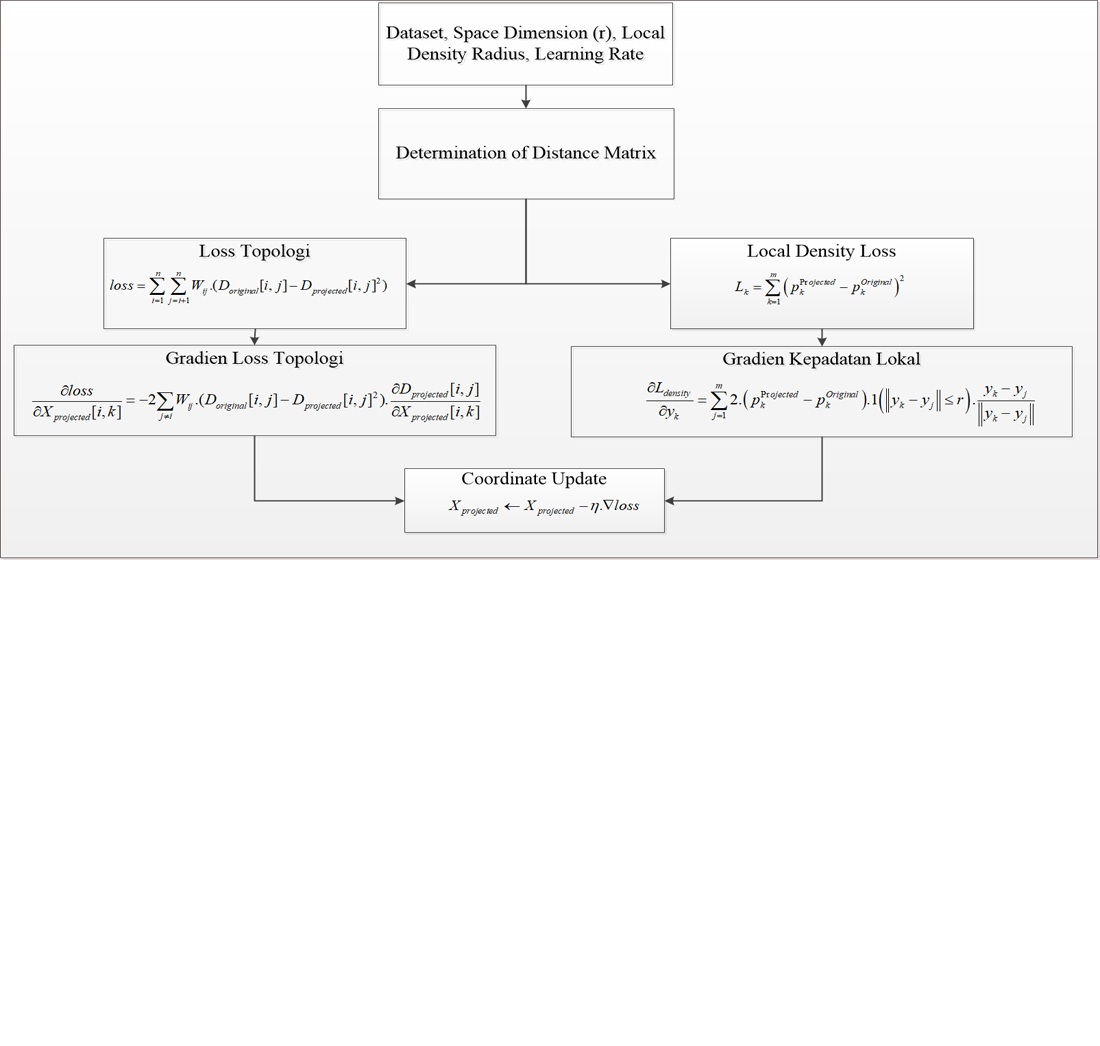
The object of this study is the clustering of water quality data characterized by complex distribution patterns, irregular cluster shapes, and local density variations. The main problem encountered is the limitation of conventional methods such as K-means in achieving optimal cluster separation when the data has uneven distribution, overlap between clusters, and density imbalance. To overcome this, a clustering approach based on local density optimization (LDO) was developed, integrated with principal component analysis (PCA) for dimension reduction and Pasca distance (PaDi) to adjust distance calculations according to local density variations. In this approach, LDO serves to improve data distribution by maintaining global topology and local density consistency before performing cluster formation using the K-means algorithm. Testing on a real water quality dataset shows that the combination of PCA + LDO + PaDi + K-means achieves a Silhouette score of 0.3450, a Davies-Bouldin index of 0.9149, and a Calinski-Harabasz Index of 616.1674, which is superior to both standard K-means and PCA + K-means. This improvement was achieved due to the LDO’s ability to reduce density distortion, resulting in more compact clusters, clearer boundaries, and reduced classification errors in transition areas. The proposed approach is characterized by adaptive density-based transformation, sensitivity to local variations through PaDi, and high stability in iterations, ensuring robustness in diverse data conditions. Thus, this approach is relevant for large-scale and real-time water quality monitoring systems and can be extended to other multidimensional datasets in the environmental, industrial, and ecological fields with complex distributions, providing a strong analytical basis for decision-making and policy development

Author Biographies

Paska Marto Hasugian, Santo Thomas Catholic University

Doctoral, Doctor of Computer Science, Lecturer

Department of Data Science

Pandi Barita Nauli Simangunsong, Santo Thomas Catholic University

Doctoral, Doctor of Computer Science, Lecturer

Department of Computer Science

Sardo Pardingotan Sipayung, Santo Thomas Catholic University

Master's Degree, Master of Information Technology, Lecturer

Department of Data Science

References

  1. Wang, Q., Zhu-Tian, C., Wang, Y., Qu, H. (2022). A Survey on ML4VIS: Applying Machine Learning Advances to Data Visualization. IEEE Transactions on Visualization and Computer Graphics, 28 (12), 5134–5153. https://doi.org/10.1109/tvcg.2021.3106142
  2. Tian, D., Zhao, X., Gao, L., Liang, Z., Yang, Z., Zhang, P. et al. (2024). Estimation of water quality variables based on machine learning model and cluster analysis-based empirical model using multi-source remote sensing data in inland reservoirs, South China. Environmental Pollution, 342, 123104. https://doi.org/10.1016/j.envpol.2023.123104
  3. Hamed, M. A. R. (2019). Application of Surface Water Quality Classification Models Using Principal Components Analysis and Cluster Analysis. Journal of Geoscience and Environment Protection, 07 (06), 26–41. https://doi.org/10.4236/gep.2019.76003
  4. Jibrin, A. M., Al-Suwaiyan, M., Yaseen, Z. M., Abba, S. I. (2025). New perspective on density-based spatial clustering of applications with noise for groundwater assessment. Journal of Hydrology, 661, 133566. https://doi.org/10.1016/j.jhydrol.2025.133566
  5. Marín Celestino, A., Martínez Cruz, D., Otazo Sánchez, E., Gavi Reyes, F., Vásquez Soto, D. (2018). Groundwater Quality Assessment: An Improved Approach to K-Means Clustering, Principal Component Analysis and Spatial Analysis: A Case Study. Water, 10 (4), 437. https://doi.org/10.3390/w10040437
  6. Maheshwari, R., Mohanty, S. K., Mishra, A. C. (2023). DCSNE: Density-based Clustering using Graph Shared Neighbors and Entropy. Pattern Recognition, 137, 109341. https://doi.org/10.1016/j.patcog.2023.109341
  7. Yang, Y., Cai, J., Yang, H., Zhao, X. (2022). Density clustering with divergence distance and automatic center selection. Information Sciences, 596, 414–438. https://doi.org/10.1016/j.ins.2022.03.027
  8. Chowdhury, H. A., Bhattacharyya, D. K., Kalita, J. K. (2021). UIFDBC: Effective density based clustering to find clusters of arbitrary shapes without user input. Expert Systems with Applications, 186, 115746. https://doi.org/10.1016/j.eswa.2021.115746
  9. Zhao, J., Wang, G., Pan, J.-S., Fan, T., Lee, I. (2023). Density peaks clustering algorithm based on fuzzy and weighted shared neighbor for uneven density datasets. Pattern Recognition, 139, 109406. https://doi.org/10.1016/j.patcog.2023.109406
  10. Wang, Y., Qian, J., Hassan, M., Zhang, X., Zhang, T., Yang, C. et al. (2024). Density peak clustering algorithms: A review on the decade 2014–2023. Expert Systems with Applications, 238, 121860. https://doi.org/10.1016/j.eswa.2023.121860
  11. Ding, S., Li, M., Huang, T., Zhu, W. (2024). Local density based on weighted K-nearest neighbors for density peaks clustering. Knowledge-Based Systems, 305, 112609. https://doi.org/10.1016/j.knosys.2024.112609
  12. Yang, H., Wang, W., Cai, J., Wang, J., Li, Y., Xun, Y., Zhao, X. (2025). Three-way clustering based on the graph of local density trend. International Journal of Approximate Reasoning, 182, 109422. https://doi.org/10.1016/j.ijar.2025.109422
  13. Kopczewska, K. (2025). Analysing local spatial density of human activity with quick density clustering (QDC) algorithm. Computers, Environment and Urban Systems, 119, 102289. https://doi.org/10.1016/j.compenvurbsys.2025.102289
  14. Gupta, V., Gupta, S. K., Shetty, A. (2024). Fractal-based supervised approach for dimensionality reduction of hyperspectral images. Computers & Geosciences, 193, 105733. https://doi.org/10.1016/j.cageo.2024.105733
  15. Ge, J., Liao, Y., Zhang, B. (2024). Resistance distances and the Moon-type formula of a vertex-weighted complete split graph. Discrete Applied Mathematics, 359, 10–15. https://doi.org/10.1016/j.dam.2024.07.040
  16. Song, J., Daley, T., McNeany, J., Kamaleswaran, R., Stecenko, A. (2024). 682 A machine learning approach with silhouette scoring of continuous glucose monitoring enables repeat measure assessment of changes in the glycemic profile in cystic fibrosis. Journal of Cystic Fibrosis, 23, S381–S382. https://doi.org/10.1016/s1569-1993(24)01520-0
  17. Ros, F., Riad, R., Guillaume, S. (2023). PDBI: A partitioning Davies-Bouldin index for clustering evaluation. Neurocomputing, 528, 178–199. https://doi.org/10.1016/j.neucom.2023.01.043
  18. Passarella, R., Noor, T. M., Arsalan, O., Adenan, M. S. (2024). Anomaly detection in commercial aircraft landing at SSK II airport using clustering method. Aerospace Traffic and Safety, 1 (2-4), 141–154. https://doi.org/10.1016/j.aets.2024.12.004
  19. Marto Hasugian, P., Mawengkang, H., Sihombing, P., Efendi, S. (2025). Development of distance formulation for high-dimensional data visualization in multidimensional scaling. Bulletin of Electrical Engineering and Informatics, 14 (2), 1178–1189. https://doi.org/10.11591/eei.v14i2.8738
  20. Zhu, M.-X., Lv, X.-J., Chen, W.-J., Li, C.-N., Shao, Y.-H. (2022). Local density peaks clustering with small size distance matrix. Procedia Computer Science, 199, 331–338. https://doi.org/10.1016/j.procs.2022.01.040
Development of a local density optimization approach for structure improvement and cluster separation in water quality data

Downloads

Published

2025-10-30

How to Cite

Hasugian, P. M., Simangunsong, P. B. N., & Sipayung, S. P. (2025). Development of a local density optimization approach for structure improvement and cluster separation in water quality data. Eastern-European Journal of Enterprise Technologies, 5(4 (137), 18–30. https://doi.org/10.15587/1729-4061.2025.337049

Issue

Vol. 5 No. 4 (137) (2025): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2025 Paska Marto Hasugian, Pandi Barita Nauli Simangunsong, Sardo Pardingotan Sipayung

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.