Розробка підходу до оптимізації локальної густини для покращення структури та розділення кластерів у даних про якість води

Автор(и)

DOI:

https://doi.org/10.15587/1729-4061.2025.337049

Ключові слова:

якість води, кластеризація без вчителя, перетворення щільності, аналіз головних компонентів, відстань Паска

Анотація

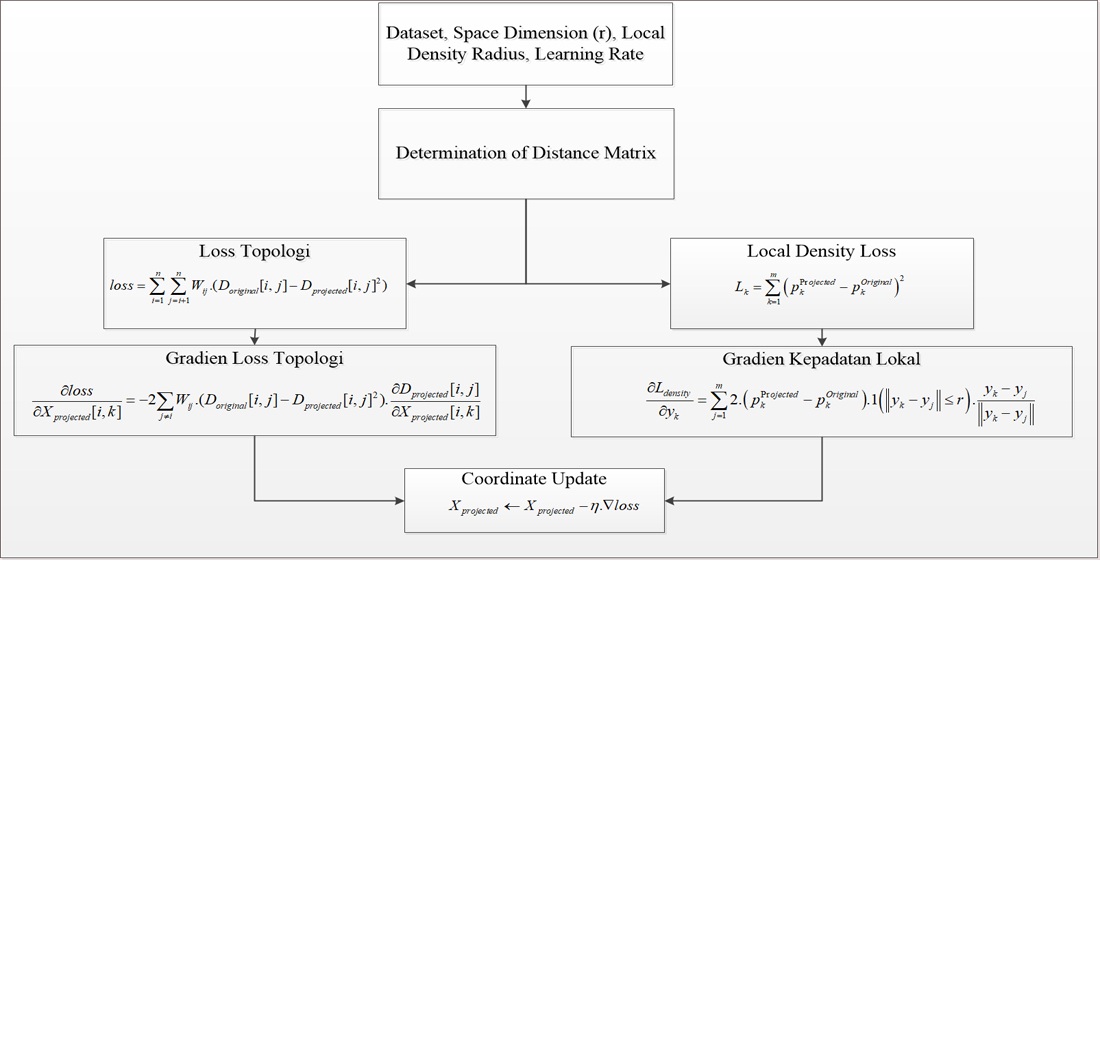
Об’єктом цього дослідження є кластеризація даних про якість води, що характеризуються складними моделями розподілу, неправильними формами кластерів та локальними варіаціями щільності. Основною проблемою, що виникає, є обмеження традиційних методів, таких як K-середніх, у досягненні оптимального розділення кластерів, коли дані мають нерівномірний розподіл, перекриття між кластерами та дисбаланс щільності. Щоб подолати це, було розроблено підхід до кластеризації, заснований на локальній оптимізації щільності (LDO), інтегрований з аналізом головних компонентів (PCA) для зменшення розмірності та відстанню Паска (PaDi) для коригування розрахунків відстані відповідно до локальних варіацій щільності. У цьому підході LDO служить для покращення розподілу даних, підтримуючи глобальну топологію та локальну узгодженість щільності перед виконанням формування кластерів за допомогою алгоритму K-середніх. Тестування на реальному наборі даних про якість води показує, що комбінація PCA + LDO + PaDi + K-середніх досягає показника показник силуету 0,3450, індексу Девіса-Боулдена 0,9149 та індексу Калінського-Харабаша 616,1674, що перевершує як стандартні K-середні, так і PCA + K-середні. Цього покращення було досягнуто завдяки здатності LDO зменшувати спотворення щільності, що призводить до більш компактних кластерів, чіткіших меж та зменшення помилок класифікації в перехідних областях. Запропонований підхід характеризується адаптивним перетворенням на основі щільності, чутливістю до локальних варіацій через PaDi та високою стабільністю в ітераціях, що забезпечує стійкість у різноманітних умовах даних. Таким чином, цей підхід є актуальним для великомасштабних систем моніторингу якості води в режимі реального часу та може бути поширений на інші багатовимірні набори даних у екологічній, промисловій та екологічній сферах зі складними розподілами, забезпечуючи міцну аналітичну основу для прийняття рішень та розробки політики

Біографії авторів

Paska Marto Hasugian, Santo Thomas Catholic University

Doctoral, Doctor of Computer Science, Lecturer

Department of Data Science

Pandi Barita Nauli Simangunsong, Santo Thomas Catholic University

Doctoral, Doctor of Computer Science, Lecturer

Department of Computer Science

Sardo Pardingotan Sipayung, Santo Thomas Catholic University

Master's Degree, Master of Information Technology, Lecturer

Department of Data Science

Посилання

  1. Wang, Q., Zhu-Tian, C., Wang, Y., Qu, H. (2022). A Survey on ML4VIS: Applying Machine Learning Advances to Data Visualization. IEEE Transactions on Visualization and Computer Graphics, 28 (12), 5134–5153. https://doi.org/10.1109/tvcg.2021.3106142
  2. Tian, D., Zhao, X., Gao, L., Liang, Z., Yang, Z., Zhang, P. et al. (2024). Estimation of water quality variables based on machine learning model and cluster analysis-based empirical model using multi-source remote sensing data in inland reservoirs, South China. Environmental Pollution, 342, 123104. https://doi.org/10.1016/j.envpol.2023.123104
  3. Hamed, M. A. R. (2019). Application of Surface Water Quality Classification Models Using Principal Components Analysis and Cluster Analysis. Journal of Geoscience and Environment Protection, 07 (06), 26–41. https://doi.org/10.4236/gep.2019.76003
  4. Jibrin, A. M., Al-Suwaiyan, M., Yaseen, Z. M., Abba, S. I. (2025). New perspective on density-based spatial clustering of applications with noise for groundwater assessment. Journal of Hydrology, 661, 133566. https://doi.org/10.1016/j.jhydrol.2025.133566
  5. Marín Celestino, A., Martínez Cruz, D., Otazo Sánchez, E., Gavi Reyes, F., Vásquez Soto, D. (2018). Groundwater Quality Assessment: An Improved Approach to K-Means Clustering, Principal Component Analysis and Spatial Analysis: A Case Study. Water, 10 (4), 437. https://doi.org/10.3390/w10040437
  6. Maheshwari, R., Mohanty, S. K., Mishra, A. C. (2023). DCSNE: Density-based Clustering using Graph Shared Neighbors and Entropy. Pattern Recognition, 137, 109341. https://doi.org/10.1016/j.patcog.2023.109341
  7. Yang, Y., Cai, J., Yang, H., Zhao, X. (2022). Density clustering with divergence distance and automatic center selection. Information Sciences, 596, 414–438. https://doi.org/10.1016/j.ins.2022.03.027
  8. Chowdhury, H. A., Bhattacharyya, D. K., Kalita, J. K. (2021). UIFDBC: Effective density based clustering to find clusters of arbitrary shapes without user input. Expert Systems with Applications, 186, 115746. https://doi.org/10.1016/j.eswa.2021.115746
  9. Zhao, J., Wang, G., Pan, J.-S., Fan, T., Lee, I. (2023). Density peaks clustering algorithm based on fuzzy and weighted shared neighbor for uneven density datasets. Pattern Recognition, 139, 109406. https://doi.org/10.1016/j.patcog.2023.109406
  10. Wang, Y., Qian, J., Hassan, M., Zhang, X., Zhang, T., Yang, C. et al. (2024). Density peak clustering algorithms: A review on the decade 2014–2023. Expert Systems with Applications, 238, 121860. https://doi.org/10.1016/j.eswa.2023.121860
  11. Ding, S., Li, M., Huang, T., Zhu, W. (2024). Local density based on weighted K-nearest neighbors for density peaks clustering. Knowledge-Based Systems, 305, 112609. https://doi.org/10.1016/j.knosys.2024.112609
  12. Yang, H., Wang, W., Cai, J., Wang, J., Li, Y., Xun, Y., Zhao, X. (2025). Three-way clustering based on the graph of local density trend. International Journal of Approximate Reasoning, 182, 109422. https://doi.org/10.1016/j.ijar.2025.109422
  13. Kopczewska, K. (2025). Analysing local spatial density of human activity with quick density clustering (QDC) algorithm. Computers, Environment and Urban Systems, 119, 102289. https://doi.org/10.1016/j.compenvurbsys.2025.102289
  14. Gupta, V., Gupta, S. K., Shetty, A. (2024). Fractal-based supervised approach for dimensionality reduction of hyperspectral images. Computers & Geosciences, 193, 105733. https://doi.org/10.1016/j.cageo.2024.105733
  15. Ge, J., Liao, Y., Zhang, B. (2024). Resistance distances and the Moon-type formula of a vertex-weighted complete split graph. Discrete Applied Mathematics, 359, 10–15. https://doi.org/10.1016/j.dam.2024.07.040
  16. Song, J., Daley, T., McNeany, J., Kamaleswaran, R., Stecenko, A. (2024). 682 A machine learning approach with silhouette scoring of continuous glucose monitoring enables repeat measure assessment of changes in the glycemic profile in cystic fibrosis. Journal of Cystic Fibrosis, 23, S381–S382. https://doi.org/10.1016/s1569-1993(24)01520-0
  17. Ros, F., Riad, R., Guillaume, S. (2023). PDBI: A partitioning Davies-Bouldin index for clustering evaluation. Neurocomputing, 528, 178–199. https://doi.org/10.1016/j.neucom.2023.01.043
  18. Passarella, R., Noor, T. M., Arsalan, O., Adenan, M. S. (2024). Anomaly detection in commercial aircraft landing at SSK II airport using clustering method. Aerospace Traffic and Safety, 1 (2-4), 141–154. https://doi.org/10.1016/j.aets.2024.12.004
  19. Marto Hasugian, P., Mawengkang, H., Sihombing, P., Efendi, S. (2025). Development of distance formulation for high-dimensional data visualization in multidimensional scaling. Bulletin of Electrical Engineering and Informatics, 14 (2), 1178–1189. https://doi.org/10.11591/eei.v14i2.8738
  20. Zhu, M.-X., Lv, X.-J., Chen, W.-J., Li, C.-N., Shao, Y.-H. (2022). Local density peaks clustering with small size distance matrix. Procedia Computer Science, 199, 331–338. https://doi.org/10.1016/j.procs.2022.01.040
Розробка підходу до оптимізації локальної густини для покращення структури та розділення кластерів у даних про якість води

##submission.downloads##

Опубліковано

2025-10-30

Як цитувати

Hasugian, P. M., Simangunsong, P. B. N., & Sipayung, S. P. (2025). Розробка підходу до оптимізації локальної густини для покращення структури та розділення кластерів у даних про якість води. Eastern-European Journal of Enterprise Technologies, 5(4 (137), 18–30. https://doi.org/10.15587/1729-4061.2025.337049

Номер

Том 5 № 4 (137) (2025): Математика та кібернетика - прикладні аспекти

Розділ

Математика та кібернетика - прикладні аспекти

Ліцензія

Авторське право (c) 2025 Paska Marto Hasugian, Pandi Barita Nauli Simangunsong, Sardo Pardingotan Sipayung

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.

Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.