Construction of mathematical models of heat exchange for digital devices with local near-surface and internal heating

Authors

DOI:

https://doi.org/10.15587/1729-4061.2025.341525

Keywords:

temperature field, thermal conductivity of material, thermal stability of structures, heat-sensitive material, thermally-active zone

Abstract

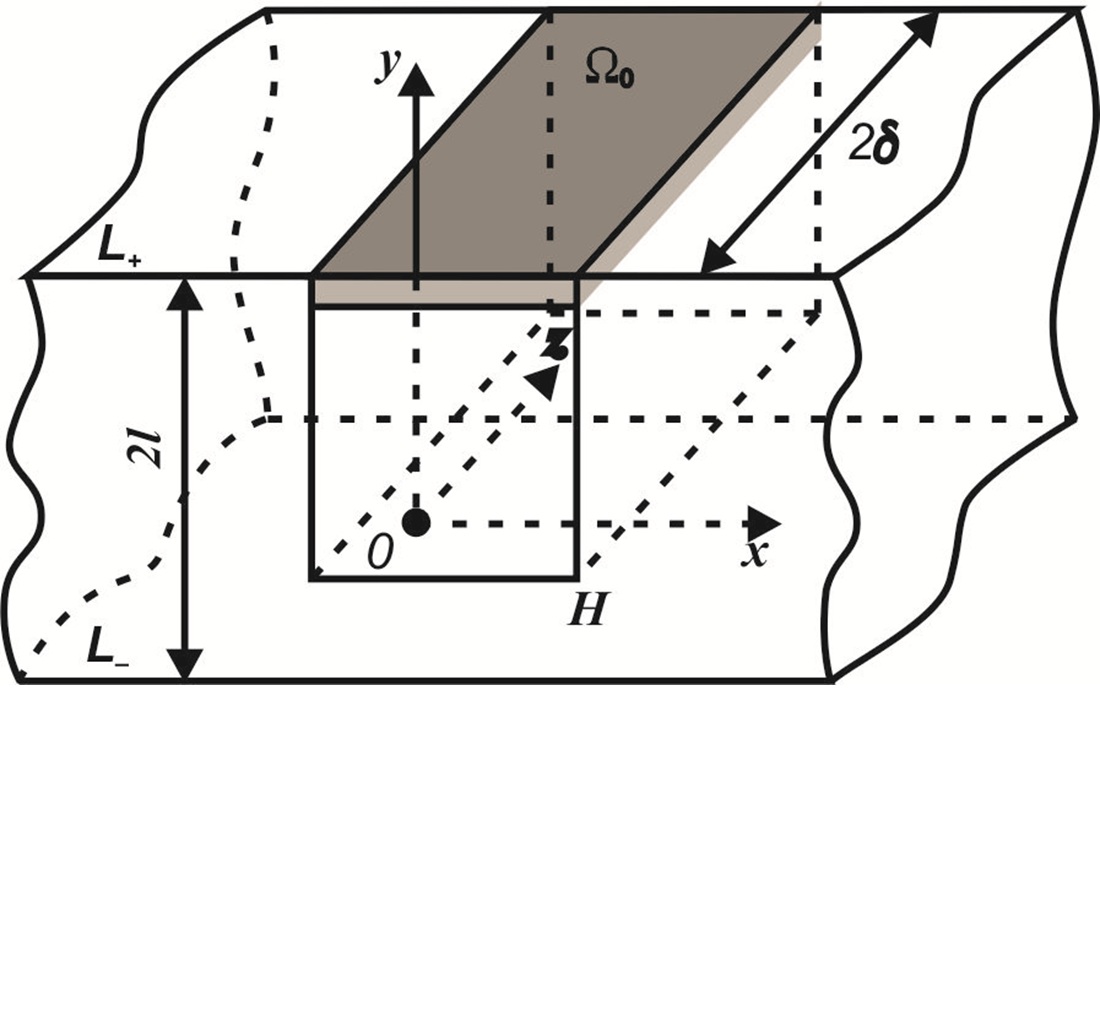
This study investigates heat exchange processes for thermally sensitive media with local near-surface and internal heating. As a result of the thermal load, significant temperature gradients arise. To establish temperature regimes for effective operation of electronic devices, linear and nonlinear mathematical models for determining the temperature field have been constructed, which could allow further analysis of temperature regimes.

Based on the stated linear and nonlinear boundary value problems of thermal conductivity, their analytical and numerical solutions have been derived. Using these solutions, numerical calculations of the temperature distribution in spatial coordinates for given geometric and thermophysical parameters have been performed. Reliability of the results has been confirmed by experimental findings and the determined numerical values of temperature distribution in the medium.

For an effective description of local heating, the theory of generalized functions was used. A technique for linearizing nonlinear mathematical models has been introduced. As a result, linear second-order differential equations with partial derivatives and a singular right-hand side have been derived.

The numerical results reflect the temperature distribution in the medium in spatial coordinates for the given geometric and thermophysical parameters. The number of divisions of the interval (0; x*) was chosen to be 9, which made it possible to derive numerical values of temperature with an accuracy of 10–6. The obtained numerical values of temperature for silicon under a linear temperature dependence of the thermal conductivity coefficient differ from the results obtained for its constant value by 2%.

Author Biographies

Vasyl Havrysh, Lviv Polytechnic National University

Doctor of Technical Sciences, Professor

Department of Software

Svitlana Yatsyshyn, Ukrainian National Forestry University

PhD

Department of Software Engineering

Viktoria Maikher, Lviv Polytechnic National University

PhD

Department of Software

Oksana Hrytsai, Lviv Polytechnic National University

PhD

Department of Software

Fedir Honchar, Lviv Polytechnic National University

PhD

Department of General Physics

References

  1. Cui, Y., Li, M., Hu, Y. (2020). Emerging interface materials for electronics thermal management: experiments, modeling, and new opportunities. Journal of Materials Chemistry C, 8 (31), 10568–10586. https://doi.org/10.1039/c9tc05415d
  2. Pannucharoenwong, N., Rattanadecho, P., Echaroj, S., Hemathulin, S., Nabudda, K. (2020). The Investigation of Heat Absorber on the Efficiency of Slanted Double-Slope Solar Distillation Unit. International Journal of Heat and Technology, 38 (1), 171–179. https://doi.org/10.18280/ijht.380119
  3. Zhang, Z., Sun, Y., Cao, X., Xu, J., Yao, L. (2024). A slice model for thermoelastic analysis of porous functionally graded material sandwich beams with temperature-dependent material properties. Thin-Walled Structures, 198, 111700. https://doi.org/10.1016/j.tws.2024.111700
  4. Zhang, Z., Zhou, D., Fang, H., Zhang, J., Li, X. (2021). Analysis of layered rectangular plates under thermo-mechanical loads considering temperature-dependent material properties. Applied Mathematical Modelling, 92, 244–260. https://doi.org/10.1016/j.apm.2020.10.036
  5. Filymonenko, N. M., Filimonenko, K. V. (2020). Analysis of capability for improvement of basic mathematical model of electrode of ferro-alloy furnace. Scientific journals of Volodymyr Dahl East Ukrainian National University, 7 (263), 53–57. https://doi.org/10.33216/1998-7927-2020-263-7-53-57
  6. Sadiq Al-Baghdadi, M. A. R., Noor, Z. M. H., Zeiny, A., Burns, A., Wen, D. (2020). CFD analysis of a nanofluid-based microchannel heat sink. Thermal Science and Engineering Progress, 20, 100685. https://doi.org/10.1016/j.tsep.2020.100685
  7. Liu, J., Zhang, Y., Zhang, D., Jiao, S., Zhang, Z., Zhou, Z. (2020). Model development and performance evaluation of thermoelectric generator with radiative cooling heat sink. Energy Conversion and Management, 216, 112923. https://doi.org/10.1016/j.enconman.2020.112923
  8. Hu, S., Li, C., Zhou, Z., Liu, B., Zhang, Y., Yang, M. et al. (2023). Nanoparticle-enhanced coolants in machining: mechanism, application, and prospects. Frontiers of Mechanical Engineering, 18 (4). https://doi.org/10.1007/s11465-023-0769-8
  9. Peng, X., Li, X., Gong, Z., Zhao, X., Yao, W. (2022). A deep learning method based on partition modeling for reconstructing temperature field. International Journal of Thermal Sciences, 182, 107802. https://doi.org/10.1016/j.ijthermalsci.2022.107802
  10. Ren, Y., Huo, R., Zhou, D., Zhang, Z. (2022). Thermo-Mechanical Buckling Analysis of Restrained Columns Under Longitudinal Steady-State Heat Conduction. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 47 (3), 1411–1423. https://doi.org/10.1007/s40996-022-01020-7
  11. Zhou, Y., Wu, S., Long, Y., Zhu, P., Wu, F., Liu, F., Murugadoss, V. et al. (2020). Recent Advances in Thermal Interface Materials. ES Materials & Manufacturing, 7, 4–24. https://doi.org/10.30919/esmm5f717
  12. Chu, Y.-M., Shah, F., Khan, M. I., Kadry, S., Abdelmalek, Z., Khan, W. A. (2020). Cattaneo-Christov double diffusions (CCDD) in entropy optimized magnetized second grade nanofluid with variable thermal conductivity and mass diffusivity. Journal of Materials Research and Technology, 9 (6), 13977–13987. https://doi.org/10.1016/j.jmrt.2020.09.101
  13. Sebald, G., Komiya, A., Jay, J., Coativy, G., Lebrun, L. (2020). Regenerative cooling using elastocaloric rubber: Analytical model and experiments. Journal of Applied Physics, 127 (9). https://doi.org/10.1063/1.5132361
  14. Liu, H., Yu, J., Wang, R. (2023). Dynamic compact thermal models for skin temperature prediction of portable electronic devices based on convolution and fitting methods. International Journal of Heat and Mass Transfer, 210, 124170. https://doi.org/10.1016/j.ijheatmasstransfer.2023.124170
  15. Ghannad, M., Yaghoobi, M. P. (2015). A thermoelasticity solution for thick cylinders subjected to thermo-mechanical loads under various boundary conditions. International Journal of Advanced Design & Manufacturing Technology, 8 (4). Available at: https://sanad.iau.ir/journal/admt/Article/534941?jid=534941
  16. Havrysh, V. І. (2015). Nonlinear Boundary-Value Problem of Heat Conduction for a Layered Plate with Inclusion. Materials Science, 51 (3), 331–339. https://doi.org/10.1007/s11003-015-9846-4
  17. Havrysh, V. І. (2017). Investigation of Temperature Fields in a Heat-Sensitive Layer with Through Inclusion. Materials Science, 52 (4), 514–521. https://doi.org/10.1007/s11003-017-9984-y
  18. Havrysh, V. I., Kosach, A. I. (2012). Boundary-value problem of heat conduction for a piecewise homogeneous layer with foreign inclusion. Materials Science, 47(6), 773–782. https://doi.org/10.1007/s11003-012-9455-4
  19. Gavrysh, V., Tushnytskyy, R., Pelekh, Y., Pukach, P., Baranetskyi, Y. (2017). Mathematical model of thermal conductivity for piecewise homogeneous elements of electronic systems. 2017 14th International Conference The Experience of Designing and Application of CAD Systems in Microelectronics (CADSM), 333–336. https://doi.org/10.1109/cadsm.2017.7916146
Construction of mathematical models of heat exchange for digital devices with local near-surface and internal heating

Downloads

Published

2025-10-31

How to Cite

Havrysh, V., Yatsyshyn, S., Maikher, V., Hrytsai, O., & Honchar, F. (2025). Construction of mathematical models of heat exchange for digital devices with local near-surface and internal heating. Eastern-European Journal of Enterprise Technologies, 5(5 (137), 31–40. https://doi.org/10.15587/1729-4061.2025.341525

Issue

Vol. 5 No. 5 (137) (2025): Applied physics

Section

Applied physics

License

Copyright (c) 2025 Vasyl Havrysh, Svitlana Yatsyshyn, Viktoria Maikher, Oksana Hrytsai, Fedir Honchar

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.