Determining the frequency of transverse oscillations of an elastically fixed disk of a circular saw
DOI:
https://doi.org/10.15587/1729-4061.2023.285516Keywords:
circular saw, transverse oscillations, ring plate, natural frequency, elastic fasteningAbstract
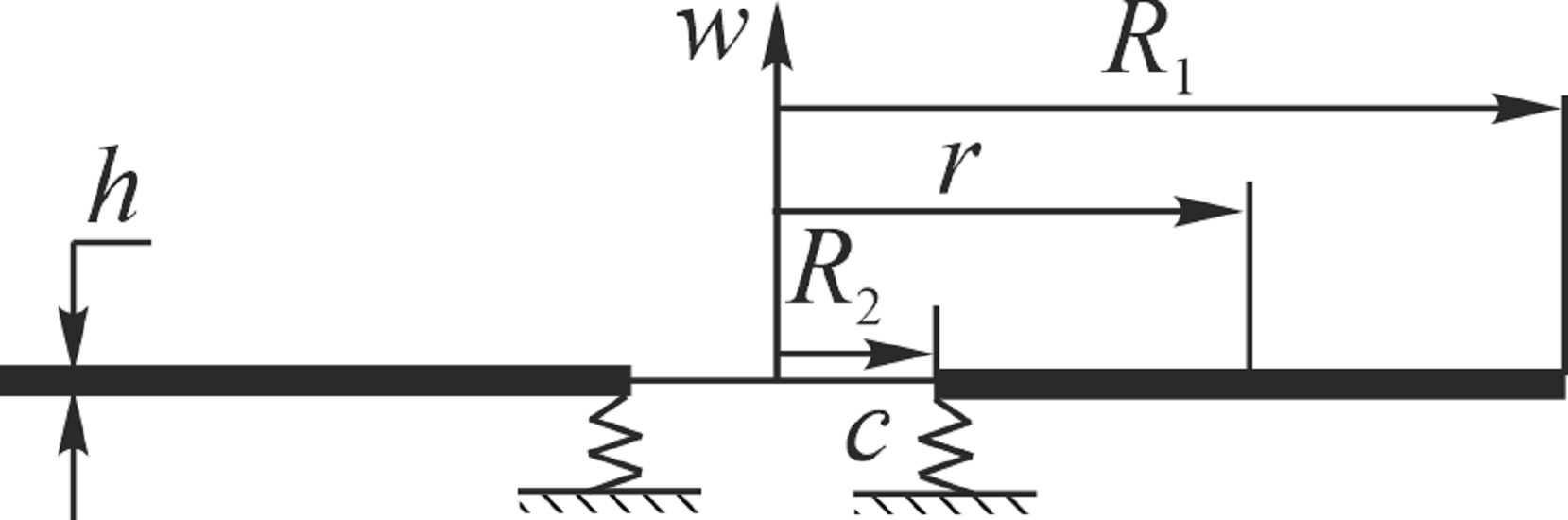
The object of the study is a circular saw blade. An annular plate of constant thickness with a free outer contour and a fixed inner contour was taken as the calculation scheme of the saw blade. The real conditions for fixing the internal circuit correspond to the elastic fixing of the saw blade with clamping flanges on the shaft of the machine. For the accepted calculation scheme of the circular saw, the dynamic model was a fourth-order nonlinear differential equation of the transverse oscillations of the annular plate with the corresponding boundary conditions. The rotation of the circular saw was taken into account in the dynamic model due to the radial force in the middle surface of the ring plate. This force arises as a result of the action of centrifugal forces during the rotation of the saw blade. The solution to the fourth-order nonlinear differential equation was constructed using the Bubnov-Galyorkin numerical method. The boundary conditions for constructing the solution were as follows: the outer contour of the saw disk was considered free; the inner contour of the saw disk – elastically fixed with a certain stiffness coefficient.
The solution was implemented in the Maple 15 mathematical environment in the form of a developed program. According to the obtained frequency equation, the values of cyclic and natural frequencies of transverse oscillations of circular saw disks of different thicknesses with the same radius of the inner contour and three values of the radii of the outer contour were determined: 150 mm, 200 m, and 250 mm. The effect of the rigidity of the internal contour fixing and the angular speed of rotation of the saw blade on the natural frequencies of transverse oscillations was studied. The study was performed for saw disks in the case of oscillations with one, two, and three nodal diameters. It was established that the rigidity of the internal contour of the saw blade has the greatest influence on the natural frequency of transverse oscillations with one nodal diameter
References
- Dzyuba, L. F., Chmyr, O. Y., Menshykova, O. V., LishchynskaK. І. (2022). Simulation of transverse oscillations of the cutting mechanism of the circular saw machine. Scientific Bulletin of UNFU, 32 (4), 55–59. doi: https://doi.org/10.36930/40320409
- Pylypchuk, M. I., Andrievskij, P. V. (2009). Directions of perfection of constructions of machine-tools forsawing of logs by round saws. Scientific Bulletin of UNFU, 19.9, 111–118. Available at: https://nv.nltu.edu.ua/Archive/2009/19_9/111_Pylypczuk_19_9.pdf
- Taras, V. I., Pylypchuk, M. I., Salovsky, S. A., Lisak, A. V. (2018). Substantiation of designing parameters of the round saw with combined crown gear. Scientific Bulletin of UNFU, 28 (10), 101–107. doi: https://doi.org/10.15421/40281021
- Yan, X., Cui, Y., Qiu, H., Ding, T., Zhu, N., Wang, B. (2023). The Transverse Vibration Characteristics of Circular Saw Blade on Mobile Cantilever-Type CNC Sawing Machine. Machines, 11 (5), 549. doi: https://doi.org/10.3390/machines11050549
- Pohl, M., Rose, M. (2016). Piezoelectric shunt damping of a circular saw blade with autonomous power supply for noise and vibration reduction. Journal of Sound and Vibration, 361, 20–31. doi: https://doi.org/10.1016/j.jsv.2015.09.021
- Svoreň, J., Javorek, L., Droba, A., Krajčovičová, M. (2015). Determination of critical rotational speed of saw blades by using various methods. Pro Ligno, 11 (4), 478–486. Available at: http://www.proligno.ro/en/articles/2015/4/Svoren_final.pdf
- Gospodarič, B., Bučar, B., Fajdiga, G. (2014). Active vibration control of circular saw blades. European Journal of Wood and Wood Products, 73 (2), 151–158. doi: https://doi.org/10.1007/s00107-014-0874-9
- Cristóvão, L., Ekevad, M., Grönlund, A. (2012). Natural frequencies of roll-tensioned circular sawblades: effects of roller loads, number of grooves, and groove positions. BioResources, 7 (2). doi: https://doi.org/10.15376/biores.7.2.2209-2219
- Merhar, M., Gornik Bučar, D. (2017). The Influence of Radial Slots on Dynamic Stability of Thermally Stressed Circular Saw Blade. Drvna Industrija, 68 (4), 341–349. doi: https://doi.org/10.5552/drind.2017.1739
- Feng, W., Zhang, J., Zhou, H., Di, H. (2020). Investigation on the vibration characteristics of circular saw blade with different slots. Journal of Physics: Conference Series, 1633 (1), 012006. doi: https://doi.org/10.1088/1742-6596/1633/1/012006
- Anđelić, N., Braut, S., Pavlović, A. (2018). Variation of Natural Frequencies by Circular Saw Blade Rotation. Technical Gazette, 25 (1), 10–17. doi: https://doi.org/10.17559/tv-20160210110559
- Skoblar, A., Andjelic, N., Zigulic, R. (2016). Determination of critical rotational speed of circular saws from natural frequencies of annular plate with analogous dimensions. International Journal of Quality Research, 10 (1), 177–192. doi: https://doi.org/10.18421/IJQR10.01-09
- Chemeris, O. (2013). Vibration of the circular annular plate with. Visnyk NTUU «KPI». Seriya: mashynobuduvannia, 3 (69), 98–105. Available at: https://ela.kpi.ua/handle/123456789/15643
- Trapezon, K., Trapezon, A. (2020). Construction of an algorithm to analytically solve a problem on the free vibrations of a composite plate of variable thickness. Eastern-European Journal of Enterprise Technologies, 1 (7 (103)), 26–33. doi: https://doi.org/10.15587/1729-4061.2020.191123
- Trapezon, K., Trapezon, A., Orlov, A. (2020). Analysis of free oscillations of round thin plates of variable thickness with a point support. Eastern-European Journal of Enterprise Technologies, 3 (7 (105)), 6–12. doi: https://doi.org/10.15587/1729-4061.2020.197463
- Dziuba, L. F., Menshykova, O. V., Rebezniuk, I. T. (2012). Vilni kolyvannia dyska kruhloi pylky. Visnyk SevNTU, 133, 75–78. Available at: http://virt.ldubgd.edu.ua/pluginfile.php/14588/mod_folder/content/0/Year-2012/Дзюба%20Л.Ф/St_8.pdf?forcedownload=1
- Babenko, A. Ye., Boronko, O. O., Lavrenko, Ya. I., Trubachev, S. I. (2022). Kolyvannia sterzhniv, plastyn ta obolonok. Kyiv: KPI im. Ihoria Sikorskoho, 252. Available at: https://ela.kpi.ua/bitstream/123456789/48522/1/Kolyvannia.pdf
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Lidiia Dziuba, Oksana Chmyr, Olha Menshykova, Khrystyna Lishchynska

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









