Development of an error correction method using perfect binary arrays

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.285540

Keywords:

error correction information coding, error detection, perfect binary arrays

Abstract

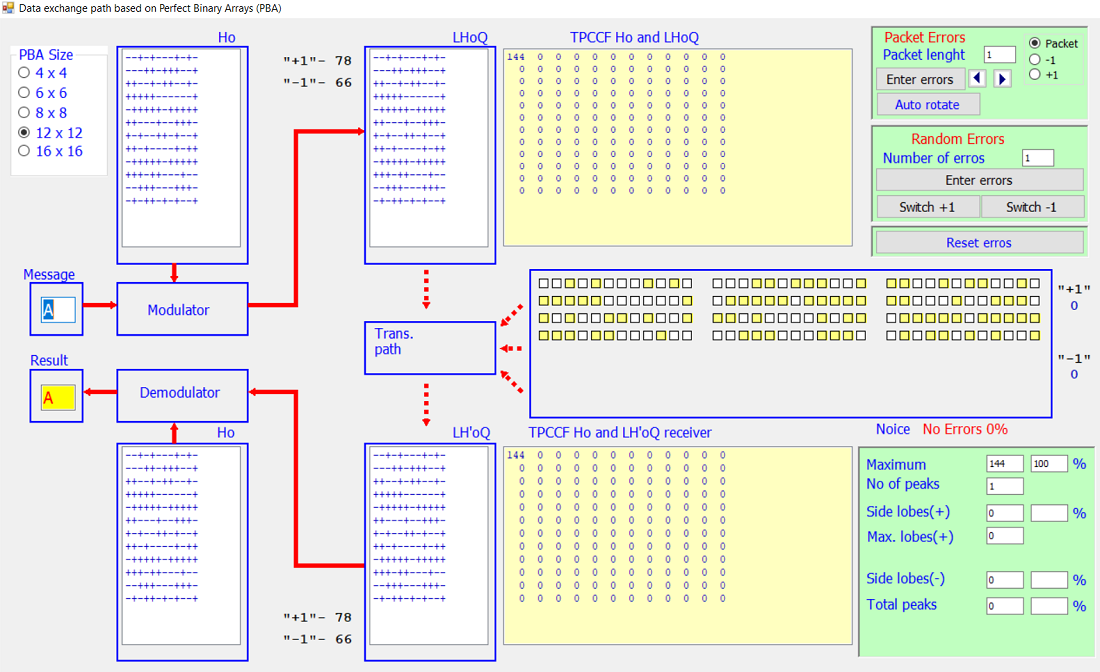
The research focuses on an innovative error correction method that uses perfect binary arrays (PBAs), a powerful mathematical tool with unique properties that make it ideal for error correction. The research is aimed at studying the impact of uncorrelated mixed-type errors in the data exchange path, which allows using it in smart technologies with limited computing capabilities. The effectiveness of the approach is confirmed by simulation and comparison with other error correction methods. In order to further study the structural, cross-correlation and distance properties of orthogonal two-dimensional codes and the correcting capabilities of the proposed method, an information technology system for data transmission based on an equivalent class of perfect binary arrays has been developed. The proposed model evaluates the performance of the error correction code based on perfect binary arrays under various conditions, including correlated and uncorrelated interference and data exchange paths. A generator of PBA of equivalent classes has been built. An experimental evaluation of the correcting ability of the proposed two-dimensional codes was carried out by simulating various pre-code situations, including packet and random errors, for the cases of correlated and uncorrelated interference. Using a graphical interface, users will be able to enter the number and type of errors, determine whether they are random or packet errors, manually or automatically, move errors through the data packet, and view intermediate results. Thus, the complex nature of this study can be positioned as a promising approach and a reliable choice in the field of error correction

Author Biographies

Pierre Murr, International University of Science and Technology in Kuwait

PhD, Assistant professor

Department of Computer Engineering

Serhii Yevseiev, National Technical University “Kharkiv Polytechnic Institute”

Doctor of Technical Sciences, Professor, Head of Department

Department of Cyber Security

Stanislav Milevskyi, National Technical University “Kharkiv Polytechnic Institute”

PhD, Associate Professor

Department of Cyber Security

Marharyta Melnyk, Private Institution "University of Science, Entrepreneurship and Technologies"

PhD, Associate Professor

Department of Cyber Security and Information Protection

Vitaliy Katsalap, The National Defence University of Ukraine named after Ivan Cherniakhovskyi

PhD, Associate Professor

Department of Information Technologies Employment and Information Security

Yurii Pribyliev, The National Defence University of Ukraine named after Ivan Cherniakhovskyi

Doctor of Technical Sciences, Associate Professor

Department of Information Technologies Employment and Information Security

Khazail Rzayev, Azerbaijan Technical University

PhD, Associate Professor

Department of Computer Technology and Cybersecurity

Andrii Bryla, Uzhhorod National University

PhD, Associate Professor

Department of Systems Analysis and Optimization

Oleksandr Shpak, Uzhhorod National University

PhD, Associate Professor

Department of Software System

Pavlo Fedorka, Uzhhorod National University

Postgraduate Student

Department of Software System

References

  1. Lin, S., Costello, D. J. (2001). Error Control Coding. Prentice-Hall. Available at: https://pg024ec.files.wordpress.com/2013/09/error-control-coding-by-shu-lin.pdf
  2. Belim, S. V., Larionov, I. B. (2020). Noise proof coding based on orthogonal functions. Journal of Physics: Conference Series, 1441 (1), 012034. doi: https://doi.org/10.1088/1742-6596/1441/1/012034
  3. Kumari, S., Gahalod, L., Changlani, S. (2022). Study of Different Types of Error Detection and Correction Code in Wireless Communication. International Journal of Scientific Research in Science, Engineering and Technology, 9 (3), 448–455. doi: https://doi.org/10.32628/ijsrset2293138
  4. Patil, A., Darkunde, N. (2018). Algorithmic Approach for Error-Correcting Capability and Decoding of Linear Codes Arising from Algebraic Geometry. Lecture Notes in Networks and Systems, 509–517. doi: https://doi.org/10.1007/978-981-13-0586-3_51
  5. Huffman, W. C., Pless, V. (2003). Fundamentals of error-correcting codes. Cambridge University Press. doi: https://doi.org/10.1017/cbo9780511807077
  6. Moon, T. K. (2005). Error Correction Coding. John Wiley & Sons. doi: https://doi.org/10.1002/0471739219
  7. Salija, P., Yamuna, B., Padmanabhan, T. R., Mishra, D. (2022). A Generic Reliability Based Direct Decoding Algorithm for Turbo Codes. Wireless Personal Communications, 125 (1), 785–801. doi: https://doi.org/10.1007/s11277-022-09577-2
  8. Sholiyi, A.O. (2011). Irregular Block Turbo Codes for Communication Systems. Swansea University. Available at: https://core.ac.uk/download/pdf/161881205.pdf
  9. Venkatesh, D. Y., Mallikarjunaiah, K., Srikantaswamy, M. (2022). A Comprehensive Review of Low Density Parity Check Encoder Techniques. Ingénierie Des Systèmes d Information, 27 (1), 11–20. doi: https://doi.org/10.18280/isi.270102
  10. Süzer, A. E., Oktal, H. (2023). A comparison analysis on forward error correction technology: a future perspective for GNSS. Aircraft Engineering and Aerospace Technology, 95 (8), 1311–1320. doi: https://doi.org/10.1108/aeat-10-2021-0319
  11. Abdelkareem, A. E. (2022). Hardware considerations of a DSP based wireless coded receiver under limited resources. 2022 International Conference on Intelligent Technology, System and Service for Internet of Everything (ITSS-IoE). doi: https://doi.org/10.1109/itss-ioe56359.2022.9990939
  12. Saiz-Adalid, L.-J., Gracia-Moran, J., Gil-Tomas, D., Baraza-Calvo, J.-C., Gil-Vicente, P.-J. (2019). Ultrafast Codes for Multiple Adjacent Error Correction and Double Error Detection. IEEE Access, 7, 151131–151143. doi: https://doi.org/10.1109/access.2019.2947315
  13. Sokolov, A. (2019). Interrelation Between the Class of Bent-Sequences and the Class of Perfect Binary Arrays. Computer Modeling and Intelligent Systems, 2353, 339–349. doi: https://doi.org/10.32782/cmis/2353-27
  14. Jedwab, J., Li, S. (2022). Group rings and character sums: tricks of the trade. arXiv. doi: https://doi.org/10.48550/arXiv.2211.11986
  15. Goresky, M., Klapper, A. (2012). Algebraic Shift Register Sequences. Cambridge University Press. doi: https://doi.org/10.1017/cbo9781139057448
  16. Hedayat, A. S., Sloane, N. J. A., Stufken, J. (1999). Orthogonal Arrays. Springer Series in Statistics. Springer. doi: https://doi.org/10.1007/978-1-4612-1478-6
  17. Yurish, S. (2019). Advances in Networks, Security and Communications: Reviews, Vol. 2. All Rights Reserved - Standard Copyright License, 145–188. Available at: https://www.lulu.com/shop/sergey-yurish/advances-in-networks-security-and-communications-reviews-vol-2/paperback/product-1gqqegqz.html?page=1&pageSize=4
  18. Jedwab, J., Mitchell, C., Piper, F., Wild, P. (1994). Perfect binary arrays and difference sets. Discrete Mathematics, 125 (1-3), 241–254. doi: https://doi.org/10.1016/0012-365x(94)90165-1
  19. Wild, P. (1988). Infinite families of perfect binary arrays. Electronics Letters, 24 (14), 845. doi: https://doi.org/10.1049/el:19880575
  20. Mazurkov, M., Chechel’nitskii, V. Y. (2003). The classes of equivalent and generative perfect binary arrays for cdma-technologies. Radioelectronics and Communications Systems, 46 (5), 40–46.
  21. Bomer, L., Antweiler, M. (1990). Two-dimensional perfect binary arrays with 64 elements. IEEE Transactions on Information Theory, 36 (2), 411–414. doi: https://doi.org/10.1109/18.52492
  22. Mazurkov, M. I., Chechel’nitskii, V. Ya., Murr, P. (2008). Information security method based on perfect binary arrays. Radioelectronics and Communications Systems, 51 (11), 612–614. doi: https://doi.org/10.3103/s0735272708110095
  23. Pless, V., Huffman, W. C. (Eds.) (1998). Handbook of Coding Theory. Elsevier.
  24. Dovgyi, S., Kopiika, O. (2022). Standard Model of System Architecture of Enterprise IT Infrastructure. Lecture Notes in Networks and Systems, 181–201. doi: https://doi.org/10.1007/978-3-031-16368-5_9
  25. Dovgiy, S., Kopiika, O., Kozlov, O. (2021). Architectures for the Information Systems, Network Resources, and Network Services (short paper). Proceedings of the Cybersecurity Providing in Information and Telecommunication Systems II. Volume I. Co-located with International Conference on Problems of Infocommunications. Science and Technology (PICST 2021), 293–301. Available at: https://ceur-ws.org/Vol-3187/short9.pdf
  26. Pohasii, S., Yevseiev, S., Zhuchenko, O., Milov, O., Lysechko, V., Kovalenko, O. et al. (2022). Development of crypto-code constructs based on LDPC codes. Eastern-European Journal of Enterprise Technologies, 2 (9 (116)), 44–59. doi: https://doi.org/10.15587/1729-4061.2022.254545
  27. Yevseiev, S., Hryshchuk, R., Molodetska, K., Nazarkevych, M., Hrytsyk, V., Milov, O. et. al.; Yevseiev, S., Hryshchuk, R., Molodetska, K., Nazarkevych, M. (Eds.) (2022). Modeling of security systems for critical infrastructure facilities. Kharkiv: РС ТЕСHNOLOGY СЕNTЕR, 196. doi: https://doi.org/10.15587/978-617-7319-57-2
Development of an error correction method using perfect binary arrays

Downloads

Published

2023-08-31

How to Cite

Murr, P., Yevseiev, S., Milevskyi, S., Melnyk, M., Katsalap, V., Pribyliev, Y., Rzayev, K., Bryla, A., Shpak, O., & Fedorka, P. (2023). Development of an error correction method using perfect binary arrays. Eastern-European Journal of Enterprise Technologies, 4(9 (124), 45–53. https://doi.org/10.15587/1729-4061.2023.285540

Issue

Vol. 4 No. 9 (124) (2023): Information and controlling system

Section

Information and controlling system

License

Copyright (c) 2023 Pierre Murr, Serhii Yevseiev, Stanislav Milevskyi, Marharyta Melnyk, Vitaliy Katsalap, Yurii Pribyliev, Khazail Rzayev, Andrii Bryla, Oleksandr Shpak, Pavlo Fedorka

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.