Devising a method to design supersonic nozzles of rocket engines by using numerical analysis methods

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.290583

Keywords:

supersonic nozzle contour optimization, liquid-propellant rocket engines, extended cells method

Abstract

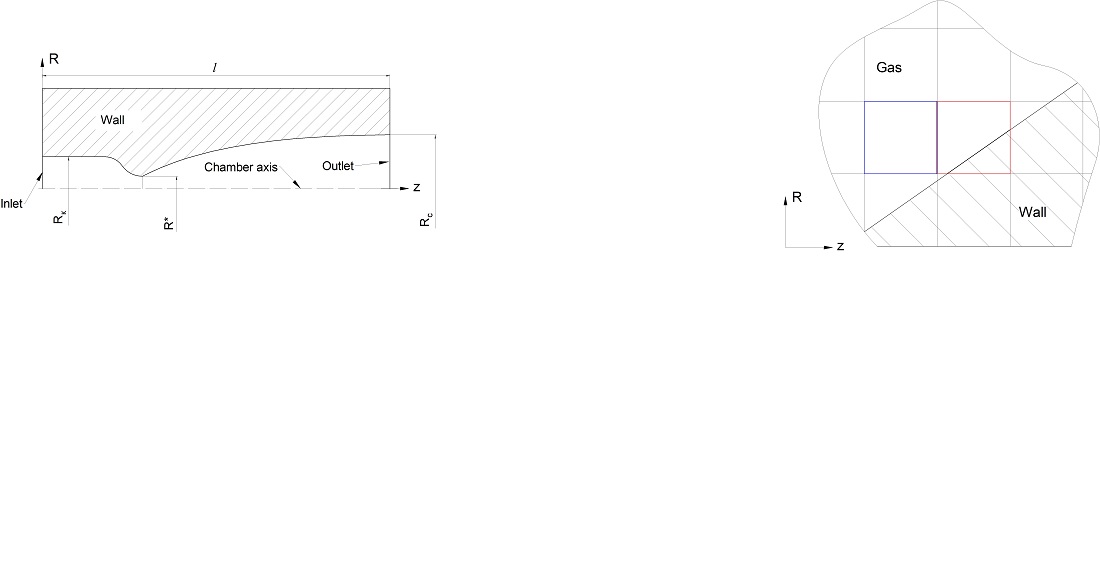
The object of research is supersonic nozzles of liquid-propellant rocket engines. The work considers the problem of the lack of an effective method for profiling the supersonic contour of the nozzle, which will generate maximum thrust. For its solution, a method is proposed, the essence of which is approximating the nozzle contour with a power-law polynomial and determining the values of its coefficients by solving a multidimensional minimization problem using numerical modeling methods. The expression for the axial component of the thrust with the opposite sign at the specified values of atmospheric pressure and radius at the nozzle section was chosen as the objective function in this paper.

Using the proposed method, contours of optimal nozzles were obtained based on polynomials of powers 2, 3, and 4, which were compared with nozzles obtained by the generally accepted Rao method. The maximum value of the relative deviation modulus calculated during the comparison did not exceed 3 %, which allows us to assert the correctness of the obtained results. The existence of such a discrepancy is explained by the difference in the numerical modeling method used. In contrast to the method of characteristics common in similar problems, the method of finite volumes of the Godunov type was used in the work. This has made it possible to reduce the sensitivity of the calculation to initial and boundary conditions and make decisions regardless of the flow regime of combustion products. In addition, the use of the extended cells method for the integration of finite volumes at the boundary of the calculation domain significantly reduced the total time of solving the problem of profiling the contour of the optimal nozzle

Author Biographies

Ivan Dubrovskiy, Oles Honchar Dnipro National University

Postgraduate Student

Department of Engine Construction

Valeriy Bucharskyi, Oles Honchar Dnipro National University

PhD, Associate Professor

Department of Engine Construction

References

  1. Biblarz, O., Sutton, G. P. (2016). Rocket propulsion elements. Wiley & Sons. Available at: https://www.wiley.com/en-us/Rocket+Propulsion+Elements%2C+9th+Edition-p-9781118753910
  2. Huang, D. H., Huzel, D. K. (1992). Modern Engineering for Design of Liquid-Propellant Rocket Engines. American Institute of Aeronautics and Astronautics. doi: https://doi.org/10.2514/4.866197
  3. de Iaco Veris, A. (2021). Fundamental Concepts of Liquid-Propellant Rocket Engines. Springer Aerospace Technology. doi: https://doi.org/10.1007/978-3-030-54704-2
  4. Schomberg, K., Olsen, J., Neely, A., Doig, G. (2019). Design of an arc-based thrust-optimized nozzle contour. Progress in Propulsion Physics – Volume 11. doi: https://doi.org/10.1051/eucass/201911517
  5. Schomberg, K., Olsen, J., Doig, G. (2016). Design of High-Area-Ratio Nozzle Contours Using Circular Arcs. Journal of Propulsion and Power, 32 (1), 188–195. doi: https://doi.org/10.2514/1.b35640
  6. Fernandes, T., Souza, A., Afonso, F. (2023). A shape design optimization methodology based on the method of characteristics for rocket nozzles. CEAS Space Journal, 15 (6), 867–879. doi: https://doi.org/10.1007/s12567-023-00511-1
  7. Frey, M., Makowka, K., Aichner, T. (2016). The TICTOP nozzle: a new nozzle contouring concept. CEAS Space Journal, 9 (2), 175–181. doi: https://doi.org/10.1007/s12567-016-0139-z
  8. Riedmann, H., Kniesner, B., Frey, M., Munz, C.-D. (2014). Modeling of combustion and flow in a single element GH2/GO2 combustor. CEAS Space Journal, 6 (1), 47–59. doi: https://doi.org/10.1007/s12567-013-0056-3
  9. Yu, K., Chen, Y., Huang, S., Lv, Z., Xu, J. (2020). Optimization and analysis of inverse design method of maximum thrust scramjet nozzles. Aerospace Science and Technology, 105, 105948. doi: https://doi.org/10.1016/j.ast.2020.105948
  10. Yu, K., Chen, Y., Huang, S., Xu, J. (2020). Inverse design method on scramjet nozzles based on maximum thrust theory. Acta Astronautica, 166, 162–171. doi: https://doi.org/10.1016/j.actaastro.2019.10.024
  11. Ferziger, J. H., Perić, M., Street, R. L. (2020). Computational Methods for Fluid Dynamics. Springer, 596. doi: https://doi.org/10.1007/978-3-319-99693-6
  12. Martins, J. R. R. A., Ning, A. (2021). Engineering Design Optimization. Cambridge: Cambridge University Press. https://doi.org/10.1017/9781108980647
  13. Barbeau, E. J. (1989). Polynomials. Springer. Available at: https://link.springer.com/book/9780387406275
  14. RD-107. Wikimedia. Available at: https://en.wikipedia.org/wiki/RD-107
  15. Dubrovskyi, I., Bucharskyi, V. (2023). Statement of the problem of designing a liquid rocket engine dual bell nozzle of the maximum thrust using the direct method of the calculus of variations. Challenges and issues of modern science. Oles Honchar Dnipro National University. Available at: https://fti.dp.ua/conf/2023/05291-0602/
  16. Bucharskyi, V., Zhang, L. H., Wan, Y. L. (2018). Improvement in Time Efficiency in Numerical Simulation for Solid Propellant Rocket Motors (SPRM). Journal of Propulsion Technology, 39 (1), 92–99. doi: https://doi.org/10.13675/j.cnki.tjjs.2018.01.010
  17. Drikakis, D., Rider, W. (2005). High-Resolution Methods for Incompressible and Low-Speed Flows. Springer. doi: https://doi.org/10.1007/b137615
  18. Shu, C.-W. (1998). Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. Advanced Numerical Approximation of Nonlinear Hyperbolic Equations, 325–432. doi: https://doi.org/10.1007/bfb0096355
  19. Toro, E. F. (2009). Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer, 724. doi: https://doi.org/10.1007/b79761
  20. Dubrovskiy, I., Bucharskyi, V. (2020). Development of a method of extended cells for the formulation of boundary conditions in numerical integration of gas dynamics equations in the domains of a curvilinear shape. Eastern-European Journal of Enterprise Technologies, 5 (7 (107)), 74–82. doi: https://doi.org/10.15587/1729-4061.2020.213795
  21. Dubrovskyi, I., Bucharskyi, V. (2023). The application of the extended cells method to simulate the flow of combustion gases in the lpre chamber. Journal of Rocket-Space Technology, 31 (4), 32–39. doi: https://doi.org/10.15421/452305
  22. Rao, G. V. R. (1958). Exhaust Nozzle Contour for Optimum Thrust. Journal of Jet Propulsion, 28 (6), 377–382. doi: https://doi.org/10.2514/8.7324
Devising a method to design supersonic nozzles of rocket engines by using numerical analysis methods

Downloads

Published

2023-12-14

How to Cite

Dubrovskiy, I., & Bucharskyi, V. (2023). Devising a method to design supersonic nozzles of rocket engines by using numerical analysis methods. Eastern-European Journal of Enterprise Technologies, 6(1 (126), 61–67. https://doi.org/10.15587/1729-4061.2023.290583

Issue

Vol. 6 No. 1 (126) (2023): Engineering technological systems

Section

Engineering technological systems

License

Copyright (c) 2023 Ivan Dubrovskiy, Valeriy Bucharskyi

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.